逆向思维在初中数学解题教学中的应用

☉湖南省洞口县石柱乡中心学校白北平

引例：九年级（3）班有50名同学参加书法、美术兴趣小组.在学校举办的“书法、美术作品竞赛”中，书法作品获奖的有40人，美术作品获奖的有31人，两种作品都没有获奖的有4人，则两种作品都获奖的有____人.

这个问题具有一定的难度，难点在于：本题涉及的数量较多，既有书法兴趣小组，又有美术兴趣小组；每个兴趣小组既有获奖的人，还有没有获奖的人.数量关系比较复杂，书法作品获奖的人既包括美术作品获奖的人又包括美术作品没有获奖的人，美术作品获奖的人既包括书法作品获奖的人又包括书法作品没有获奖的人.正因为如此，学生不知从何下手，或者由于对数量之间的关系含糊不清而致错.事实上，只要理清了题目中涉及的数量及其之间的关系，解答并不是那么困难.

通过分析我们发现，本题涉及的数量共有4种：书法作品获奖、美术作品获奖；书法作品获奖、美术作品没有获奖；书法作品没有获奖、美术作品获奖；书法作品没有获奖、美术作品没有获奖.

根据题意可知：书法作品没有获奖、美术作品没有获奖的有4人；

书法作品获奖、美术作品获奖的人数+书法作品获奖、美术作品没有获奖的人数=40；

美术作品获奖、书法作品获奖的人数+美术作品获奖、书法作品没有获奖的人数=31；

书法作品获奖、美术作品获奖的人数+书法作品获奖、美术作品没有获奖的人数+书法作品没有获奖、美术作品获奖的人数+书法作品没有获奖、美术作品没有获奖的人数=50.

设书法作品获奖、美术作品获奖的有x人，书法作品获奖、美术作品没有获奖的有y人，书法作品没有获奖、美术作品获奖的有z人，则有x+y=40，x+z=31，x+y+z+4=50即x+y+z=46.这三个方程组成三元一次方程组，求出x，即为两种作品都获奖的人数.

上述解法直接从问题的正面（作品获奖的人数）入手分析求解，比较麻烦.实际上，我们可以从作品没有获奖的人数入手求解.由于书法作品获奖的有40人，美术作品获奖的有31人，所以书法作品没有获奖的有50-40=10（人），美术作品没有获奖的有50-31=19（人）.由于两种作品都没有获奖的有4人，所以至少有一种作品没有获奖的人有10+19-4=25（人）.剩下的就是两种作品都获奖的人，有50-25=25（人）.显然这样求解十分简捷，甚至可以心算.

引例的简便求法主要得益于我们没有直接从“作品获奖的人数”这个正面思考问题，而是从“作品没有获奖的人数”这个反面思考问题，其实就是逆向思维.逆向思维也叫求异思维，是指人们在思考问题时，如果直接从正面思考思路受阻，不妨来个思维大转弯，从问题的反面入手思考，得出全新的思维方法，最终达到推陈出新、出奇制胜的效果.“司马光砸缸救人”就是一个应用逆向思维的典范.应用逆向思维解答一类从正面入手比较麻烦甚至困难的问题，往往可以化难为易，事半功倍，达到“柳暗花明”的境界.下面以例说明逆向思维在初中数学解题中的应用.

一、在证明几何命题时，不仅要看从已知条件可以得出什么结论，往往还要从结论入手进行分析，从而寻找正确的证明方法或证题途径

在证明几何命题时，无论是比较简单的几何题，还是相对复杂的几何题，我们往往要从两个方向进行分析：（1）从已知条件出发，看看能够得到什么结论；（2）从待证结论出发，看看结论成立需要什么条件，已经具备了什么条件，当然这个需要的条件往往就是从已知条件中推出的结论.

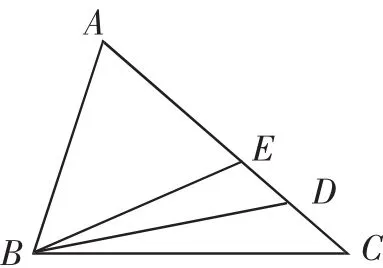
图1

例1如图1，已知在△ABC中，D、E为AC边上的点，AD=AB，∠EBD=∠DBC，求证：AD2=AE·AC.

分析：要证AD2=AE·AC，显然要通过三角形相似证明.为了便于寻找相似三角形，先将乘积式变成比例式.结合图形特征和已知条件“AD=AB”，进一步把从这个比例式可以看出，要证需要证明△ABE和△ABC这两个三角形相似.其中∠A是这两个三角形的公共角，根据三角形相似的判定方法，并结合已知条件∠EBD=∠DBC，只需再证这两个三角形中的另一对角相等即可.由已知条件AD=AB，可得∠ABD=∠ADB，即∠ABE+∠EBD=∠C+∠DBC.又∠EBD=∠DBC，则∠ABE=∠C.正好是△ABE和△ABC这两个三角形的另一对角相等.

说明：在分析几何证明题的证法或证题途径时，需要从结论入手.但在书写证明过程时，往往从已知条件出发直至推出待证的结论.

二、有些几何命题直接从正面证明非常困难，而从问题的反面入手，采用反证法往往可以化难为易，柳暗花明

大部分几何证明题往往都是从正面入手进行证明.但也有一些几何命题，如果直接从正面入手进行证明，往往非常困难.例如，证明“内角和不等于360°的多边形不是四边形”.这个几何命题看似简单，但如果从正面进行证明非常困难.如果从反面入手，运用反证法证明就简单多了，由此可见反证法在证明几何命题中的威力.

例2 如图2，已知：点D、E分别是线段AB、AC上的点，线段BE、CD相交于点O.若OB=OC，AD=AE，求证：OD=OE.

分析：本题看似简单，但如果直接从正面入手进行证明，非常困难.可以作过A、B、C三点的辅助圆，如图3所示.充分利用三角形相似进行证明，过程比较繁杂.如果从结论的反面入手，利用反证法进行证明，就简便多了.

证明：假设OD≠OE.

（1）假设OD＜OE，在线段OE上截取OF=OD，连接DE、DF、CF，如图4所示.

∠1=∠2.

图2

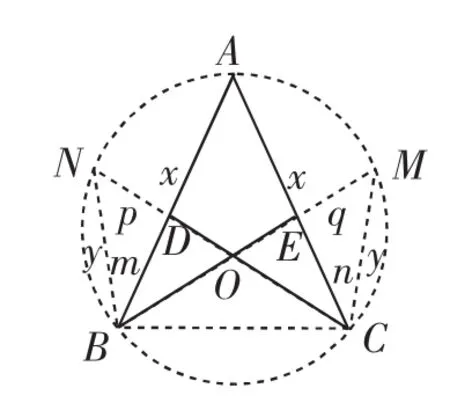
图3

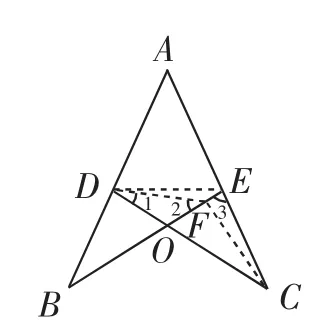
图4

易证△BOD≌△COF.则∠BDO=∠CFO.又∠CFO＞∠3，则∠BDO＞∠3.

由∠EDO＞∠1，∠1=∠2，∠2＞∠DEO，得∠EDO＞∠DEO.

则∠BDO+∠EDO＞∠3+∠DEO，即∠BDE＞∠CED.

又∠BDE与∠ADE互补，∠CED与∠AED互补，则∠ADE＜∠AED，则AE＜AD.这与已知AD=AE矛盾，因此假设不成立.

（2）假设OD＞OE，同理可证AE＞AD.仍与已知AD=AE矛盾，假设亦不成立.

综合（1）、（2）可知以上假设不成立.因此必有OD=OE.

说明：用反证法证明几何命题，首先假设结论不成立，然后从这个假设出发进行推理，得出与已知条件或定理、公理相矛盾的结论，进而假设不成立，从而原命题成立.

三、有些实际问题，直接从正面入手需要列出方程（组），运算量大，如果采用顺序倒换法思考，非常简捷

在思考数学问题的时候，受思维定式的影响，我们习惯于按照一定的顺序思考.一般情况下，很难打乱思考问题的顺序.正如我们在计量的时候，习惯于按照“从左到右、从前到后、从上到下”的顺序进行计量.实际上，有些数学问题，如果我们能打破顺序，采用顺序倒换的方法，可以使问题的解答变得简捷.

例3李飒的妈妈买了几瓶饮料，第一天，他们全家喝了全部饮料的一半零半瓶；第二天，李飒招待来家中做客的同学，又喝了第一天剩下的饮料的一半零半瓶；第三天，李飒索性将第二天所剩的饮料的一半零半瓶喝了.这三天，正好把妈妈买的全部饮料喝光，则妈妈买的饮料一共有（）瓶.

A.5B.6C.7D.8

解得y=3，这也是第一天李飒喝饮料之后所剩的饮料瓶数.再设李飒喝饮料之前，还有z瓶饮料，则解得z=7，这就是李飒喝饮料之前妈妈买的饮料瓶数，故应选C.

以上我们仅从三个方面谈了逆向思维在初中数学解题中的应用.当然，逆向思维在初中数学中的应用远不止这些.再如整式乘法中的两数和的完全公式平方（a+b）2=a2+2ab+b2与因式分解中的完全平方公式a2+2ab+b2=（a+b）2，只是将一个等式左、右两边部分对调就成了两个不同的公式，这本身就是一种逆向思维的体现.再如勾股定理与勾股定理的逆定理，也体现了一种逆向思维.在今后思考数学问题时，我们既要注意从正面思考，也要从问题的反面多想想，多进行逆向思维，从而提高我们的思维能力.W