践行“学材再建构”,从“形似”走向“神似”
——以“一元一次方程及其解法”教学为例
☉江苏省江阴市暨阳中学卞明宇
最近,我们在网上直播平台全程观摩了“自学·议论·引导”教学法第三次全国研修活动,本次活动安排了主旨演讲、专家报告、好课观摩、学术沙龙、名师示范、名师讲座等形式,我们受益很多.本文主要针对“好课观摩”中展示的一节“一元一次方程及其解法”公开课展开一些评析,先概述该课主要教学流程(含一些对话片段),再给出意见,供研讨.
一、课例概述
教学环节(一)开门见山,定义新知
教师开课后直接提问“什么是方程?请举例说明”,学生根据未知数的个数列举一些方程,并进行方程的分类,然后教师提示学生“对于一元方程,可以按照未知数的指数进行分类”,于是学生找出一些一元一次方程,教师顺势给出一元一次方程的定义,再安排学生举例,然后小组交流、小结:满足只含有一个未知数、方程两边的代数式都是整式、未知数的指数都是1这样三个条件的方程才是一元一次方程,只要有一个条件不满足,便不是一元一次方程.
接下来教师举出一个简单的一元一次方程x+1=2,并追问:在这个方程中,未知数x等于几?为什么?
生1:x=1.
师:你的理由是什么?
生1:利用等式的性质.
师:你凭什么说x=1一定是方程的解?
生1没有答出来,教师喊了另一个学生.
生2:因为x=1满足方程左、右两边相等.
教师很高兴,引导成功,顺势给出“方程的解”的定义,并指出求方程的解的过程叫作解方程.而且告知学生,解一元一次方程的基本目标就是将方程逐步转化为“x=a”的形式.
教学环节(二) 师生合作,探究解法
教师通过PPT依次出示了5个一元一次方程,由学生探究它们的解法.
例1解方程:4x=6.
例2解方程:4x+2=8.
例3解方程:2(x+1)+2x=8.
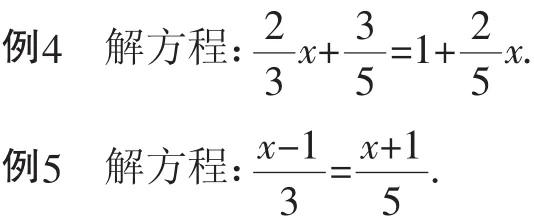
学生在上述5道例题的驱动下,分别运用等式的性质1、2达到了解出未知数的值的目标,教师在学生回答每步的变形依据之后,分别对应着给出系数化为1、移项、合并同类项、去括号、去分母等步骤.
很奇怪,学生初学一元一次方程,处理这么多的方程时,竟然只在处理例4的过程中有一个学生出现了错漏,即在去分母的过程中漏乘了“中不含分母的项“1”,教师简单点评之后,就轻轻滑过.
在例5讲评之后,师生共同小结:解一元一次方程,一般要通过去分母、去括号、移项、合并同类项、系数化为1等步骤,把一个一元一次方程转化为“x=a”的形式.并且指出,解出x=a后,可回代入原方程,根据“左边=右边”可判定x=a是否为原方程的解.
教学环节(三)课堂小结,完善板书
教师一边小结,一边完善本课板书:(如图1)
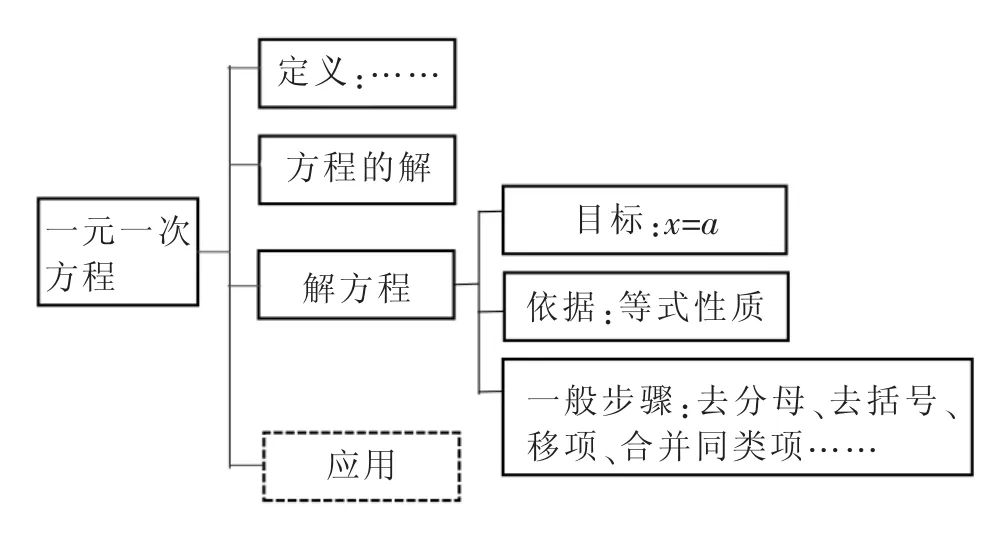
图1
再跟进如下两道练习题作为课堂反馈:
题1:什么是一元一次方程?方程x2+3x=5+x2是一元一次方程吗?
题2:什么是方程的解?有同学解方程5(x+1)-3x=4+x得到x=2,请你判断他的解是否正确.
二、评课意见
总体而言,本课体现了这次研修主题“自学·议论·引导”教学法所倡导的单元教学中“学材再建构”的教学理念.比如,执教者整合了一元一次方程的定义及相关概念、组织学生探究了多种解法的步骤,容量极大.然而,笔者认为上述处理只是对“自学·议论·引导”单元教学中“学材再建构”简单的模仿,形似,但没有走向神似.以下具体阐述三点理解.
1.注意“三个理解”的平衡,理解教材还需要理解学情和理解教学
章建跃老师近年提出的“三个理解”得到很多一线教师的积极响应,从而在教学实践中充分运用.从本课呈现的案例来看,一方面是践行“学材再建构”,打破教材中一元一次方程各小节的限制,整合学材,开展单元教学.然而其没有对学情、教学做出必要的平衡.比如,课例中5道例题都是教师给出的,一题接着一题,学生在这5个例题的驱动下,强行转弯,对多数学生来说,移项还听得很迷糊,去括号、去分母又来了,这些解法步骤都属于技能层面,多数学生都需要一定的训练量才能达到较好的理解,然而教师心中只是想着“赶进度”,缺少对这些解法的步骤的必要回顾与跟进训练,使得课堂氛围沉闷,只剩下极少数学生在“配合”教师讲步骤、说依据.
2.精准定位课时教学目标后,还要围绕教学重点与难点有教学举措
基于深刻理解数学之后“学材再建构”,需要精准定位课时教学目标,比如,本课教学目标中一个重点应该是让学生掌握解方程的目标是逐步转化为“x=a”的形式.从课堂教学实施来看,教师在课堂上并没有能很好地处理这一目标.只是把精力过多地放在解法的步骤及依据上,缺少在求出方程中未知数的值之后的“解后回顾”,因为在解后回顾时可以引导学生反思为什么要做出一些变形或化简,目的何在,所以笔者认为,每个方程解完之后应该需要强调、引导和必要的点评,将这种解后回顾作为攻克教学难点的举措.在这里还可提及著名特级教师李庾南老师在示范课“等式的性质”一课中的教学处理,整节课也是在三个生活问题驱动下学生列出三个方程,为了解这三个方程,李老师通过必要的追问,生成了多种等式的性质,最终依据等式的性质实现了求方程解的目标.整节课由问题驱动,在解决实际问题的过程中自然而然地引出等式的性质,教学用力点都放在等式性质的生成、归纳上,而其他环节则没有过多停留,体现了李老师“抓大放小”“突出重点”“详略得当”的课堂驾驭功夫.
3.课堂教学要重视究错环节,不能让“一带而过”掩饰了错例资源
从课堂观摩来看,教师围绕5个一元一次方程组织学生探究出多种解法步骤似乎很顺畅,但掩盖了可能的困难与错漏,整节课只在去分母时出现了漏乘,但是教师的处理也是“一带而过”,不利于重点、难点的突破.在这里值得一说的是,对数学教学过程中学生错误的教学应对,首先,教学预设时,要充分考虑学情,预设学生可能的错漏,在教学进程中,要注意通过恰当的方式(如示拙、稚化思维等)“诱错”,进而及时“捕错”“猎错”,并引导学生参与纠错、究错,这也就是小学数学著名特级教师华应龙老师倡导的“化错教学”.事实上,重视“化错教学”也是数学学科特点所致,因为数学概念往往具有所谓“标准形式”与“非标准形式”,学生初学一个新概念之后,往往对“标准形式”容易理解,而对一些“非标准形式”常常产生易错点,所以教师组织新概念的辨析理解时,可以出示一些“非标准形式”的习题进行训练讲评,当学生出现错漏之后,引导学生回归概念,加深学生对概念的深刻理解.
三、写在最后
得益于信息时代的便利,我们足不出户就能观摩学习到全国各地的重要教研活动.然而有些教研活动多少还存着在“哗众取宠”“名不符实”“空喊口号”“理念至上”的“假、大、空”现象.像中国教育学会中学数学教学专业委员会主办的“自学·议论·引导”全国第三次研修活动确实是难得的精品研修活动,不只是它的公益性质(不收参训教师的费用),还在于研修活动安排得务实与高效,仅从全国自发在网上观看直播的累计达到40万人次,其影响力就可见一斑.然而,我们不要忘记郑毓信教授指出的,当面对一个新的理念、口号、名词、教学法时,我们应该深入思考,这种新教法的本质是什么?与其他教学法有哪些不同?有哪些相同点?哪些值得或适合自己研习,并内化为自己的教学专业基本功?多多思考这些,也许对我们的专业精进是有利的,而不只是停留在简单的模仿阶段.

