过程教育下“立方根”教学的若干问题问答

☉浙江省象山县教育局教科研中心周林祥

发展学生的数学核心素养，是数学课堂教学的重要育人任务，而过程教育是发展学生数学核心素养的有效途径.但在以浙教版数学七年级上册3.3“立方根”为载体的研修活动中发现，课堂教学普遍存在过程教育不到位的问题.鉴于此，笔者在重复观摩与反思的基础上，以问答的形式呈现该课的几个节点问题及参考答案，供读者参考、研究.

问：该课研究的对象是什么？它是在怎样的背景下提出来的？

答：该课研究的对象是“已知x3=a（a是已知数），求x”的运算.它是在学习乘方运算的基础上，为解决形如“已知x3=a（a是已知数），求x”的需要提出来的，因为形如“已知x3=a（a是已知数），求x”的运算有丰富的现实情景.

问：该课研究的内容是什么？其地位与作用分别是什么？

答：从立方根的概念体系中可以分析出该课研究的内容是：开立方、立方根的概念，立方根的符号表示，求具体数的立方根，立方根的有关事实.其逻辑关系如图1所示.“已知x3=a（a是已知数），求x”的运算具有丰富的现实情景，用根号表示立方根的式子在实数运算中会经常遇到，求数的立方根是需要学生掌握的基本技能，由一般到一般或由特殊到特殊的研究方法在教学实践中会经常用到.

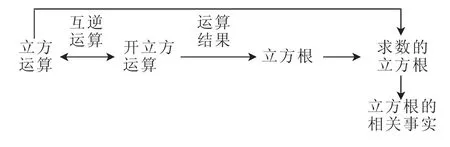
图1

问：产生“已知x3=a，求x”有哪几种方式？哪种方式比较合适？

答“：已知x3=a，求x”可以看成是从实际问题中抽象出来的，也可以看成是从“已知底数和指数3，求其幂”中演绎出来的，还可以看成是通过类比“已知x2=a，求x”得出的，也可以看成是从具体的“（？）3=8”等中归纳出来的.但采用演绎方式更能促使学生感悟立方与开立方是互逆运算.

问：数学概念有几种定义形式？定义该课中的概念可用怎样的形式？

答：数学概念的定义形式大致可分为白描、归纳和抽象这3种.例如，画出三角形，定义“这样的图形为三角形”为白描形式；画出一些包括三角形在内的多边形，定义“由三条边构成的多边形为三角形”为归纳形式；直接给出定义“由三条线段首尾相接所组成的平面图形为三角形”为抽象形式［1］.尽管立方根概念的形式特征比较明显，能从外形上直接观察和识别，并且教学要求不高，但学生对方程根的认识还没有达到一定的“深度”，而开立方与立方运算是互逆运算，所以定义立方根宜采用抽象形式.

问：根据立方根有关事实的教学性质，获得立方根的有关事实要经历哪几个步骤？

答：立方根有关事实的教学性质是原理教学，所以它要遵循原理教学的基本规范，但这些事实相对比较简单，不必经历原理教学完整的认知过程，可以在求数的立方根的基础上，引导学生通过归纳猜想得到.其基本过程可以是：用立方运算求有代表性的数的立方根→归纳猜想立方根的有关事实→表达立方根的有关事实.

问：根据上述确立的研究思想，该课研究的内容有何教育价值？

答：用演绎方式产生“已知x3=a，求x”的过程和所蕴含的从运算角度提出问题的经验，用抽象形式定义开立方和立方根的过程和所蕴含的演绎思想、符号表示思想，解释立方根概念的过程和所蕴含的从数学概念中可以分解出判定和性质两个命题的经验，用立方运算求数的立方根的过程和所蕴含的演绎思想、化归思想、间接运算的经验，求数的立方根之后反思的过程和所蕴含的归纳思想及数学活动经验等，这些对发展学生的智力、能力和个性有积极影响.

问：学生在学习该课的过程中可能会遇到哪些认知障碍？

答：尽管学生有从运算角度提出问题的经验，但从“底数指数=幂”中提出“已知x3=a，求x”，估计对部分学生来说有难度；尽管学生学过许多数学概念，但从两个方面理解概念的本质特征，大部分学生无先前经验；尽管学生有用平方运算求数的平方根的经历与经验，但学生还没有养成这种间接运算的习惯，估计部分学生不能自然地用立方运算求数的立方根；尽管学生有合情推理的经历与经验，但归纳猜想立方根的有关事实可能对部分学生来说有困难.

问：根据全面的课程目标观，该课应设置怎样的教学目标？

答：根据上述分析结果，并用“课标、教材、学生”三把筛子进行筛选，该课的教学目标可以设置为：经历回顾旧知与提出问题的过程，能从“底数指数=幂”中提出“已知x3=a，求x”的运算，能感悟研究开立方运算的意义；参与定义开立方和立方根的活动，能陈述开立方和立方根的概念，能知道开立方与立方是互逆运算，会用根号表示数的立方根，能感悟符号表示思想；参与求数的立方根的活动，会用立方运算求数的立方根，能知道立方根的有关事实，能感悟演绎思想和归纳思想，并在学习过程中有个性化的表现.

问：根据教学重、难点的含义，该课教学的重点与难点分别是什么？

答：根据该课概念的地位与作用，以及所蕴含的教育价值，其教学重点是立方根的概念和求数的立方根.因为用根号表示立方根的式子在实数运算中会经常遇到，求数的立方根是需要学生掌握的基本技能.其教学难点是立方根的概念.因为从两个方面理解立方根概念的本质特征学生无先前经验，又因为具有双重性的含义比较抽象，许多学生不能自然地把转化为“（？）3=a”.

问：教学结构是实现教学目标的通道，该课应构建怎样的教学结构？

答：根据抽象形式定义概念的认知过程观［2］，该课的教学结构可用图2表示.

图2

这是一个以数学知识发生、发展过程为载体的学生认知过程和以学生为主体的数学活动过程.这个“简单、自然、动态、和谐”的教学结构，能使学生经历完整的数学思考过程，对促进学生认知与情感的变化与发展有积极的影响.

问：“经历回顾旧知与提出问题的过程”的教学怎样操作？

答：首先，教师指出：我们知道，23=8，它是已知底数和指数求幂的运算.在“底数指数=幂”中，还能提出怎样的运算？

其次，教师解释：事实上，许多实际问题可以转化为这些运算.例如，要做一个体积为8cm3的立方体模型，它的棱长应取多少？这个问题可以转化为已知幂和指数求底数的运算.

最后，揭示课题：既然这些运算有丰富的现实情景，就有研究这些运算的必要.已知x3=a（a是已知数），怎样求x？本节课我们先来研究与之相关的问题.

解析：提出问题是概念教学不可忽视的一个环节，旨在激发学生的学习兴趣和感悟研究的必要性.该课知识的生长点是立方运算.这个经历性数学活动的内容，不仅包括立方运算，还包括从“底数指数=幂”中演绎出“已知x3=a（a是已知数），求x”的过程和所蕴含的演绎思想及开立方运算的意义.教学采用了教师价值引导下的学生自主体验的方法.它建立了新知识和旧知识之间的内在联系，能使学生感悟研究对象从哪里来和往何处去.

问“：参与定义立方根的活动”的教学怎样操作？

答：第一，教师直接给出定义：一个数的立方等于a（a是已知数），求这个数的运算，叫作开立方，这个数叫作a的立方根，也叫作a的三次方根.即：如果x3=a，那么求x的运算叫作开立方，x叫作a的立方根.

第二，教师解释：开立方与立方是互逆运算.根据立方根概念可得：若x3=a，则x是a的立方根；若x是a的立方根，则x3=a.并举例说明.

解析：尽管立方根概念的教学要求是“了解”，但用根号表示立方根的式子在实数运算中会经常遇到，它需要学生知道用根号表示立方根式子的含义.这个参与性数学活动的内容，不仅包括开立方、立方根的概念、立方根的符号表示，还包括开立方与立方是互逆运算，从数学概念中可以分解出判定和性质两个命题的经验，用根号表示立方根式子的含义，立方根的事实“（）3=a”，与的差异.教学采用了教师价值引导下的学生自主体验的方法.它揭示了立方根概念的本质特征，暗示了求数的立方根的方法，能使学生知道有双重性含义.

问“：参与求数的立方根的活动”的教学怎样操作？

答：第一，教师指出：由于开立方与立方是互逆运算，所以我们可用立方运算来求数的立方根.并示范求-的立方根的过程.

第二，教师要求学生模仿样例求下列各数的立方根：

在求上述各数的立方根之后，教师要求学生猜一猜关于数的立方根有什么结论，说说数的平方根与数的立方根有什么不同，并引导学生通过归纳得出

第三，教师要求学生先说出下列各式的意义，再计算.

最后，要求学生完成课本中的练习题，待学生完成任务后进行交互反馈与评价.

解析：用立方运算求数的立方根是整节课认知过程的后半段，求数的立方根是该课的教学重点，是需要学生掌握的基本技能，“在后继学习中会经常用到.这个参与性数学活动的内容，不仅包括求数的立方根，还包括求数的立方根的过程和所蕴含的演绎思想，立方根的有关事实，以及获得立方根有关事实的过程和所蕴含的归纳思想.教学采用了教师价值引导与学生自主建构相结合的先“放”后“收”的适度开放的方法.它能促使学生养成用立方运算间接求立方根的习惯，增强计算之后反思的意识，感悟计算过程中所蕴含的演绎思想和获得立方根有关事实过程中所蕴含的归纳思想等.

问：“参与回顾与思考的活动”的教学怎样操作？

答：首先，教师出示下列“问题清单”，并要求学生围绕“问题清单”进行回顾与思考.

（1）本节课研究了哪些内容？

（2）“已知x3=a，求x”是从哪里来的？为何学习求数的立方根？

（3）我们是用什么方法来求数的立方根的？

（4）大家在学习过程中有何感触？

其次，教师组织学生进行合作交流，同时教师边倾听、边评价.

最后，教师总结该课的研究内容与研究方法，并指出以后可用计算器来求一个数的立方根（或其近似值）.

解析：课堂总结也是整节课认知过程的后半段，旨在欣赏研究内容与研究方法，感悟研究过程和所蕴含的数学思想及积淀求数的立方根的经验.这个参与式数学活动的内容，不仅包括回顾研究内容与研究方法，还包括交流学生学习后的感悟；教学采用了“问题清单”引导下的学生独立回顾与思考基础上的交互反馈和交互反馈基础上的教师总结性讲解的方法.它有助于学生深化认识，产生个性化的想法，并对学生增强反思意识、发展语言表达能力及养成敢想、敢说、敢于创新的良好习惯有积极的影响.

以上几个问题虽不十分系统，回答可能也不全面，但它对改变当前“只教不研”的现象和发展教师的实践性智慧有积极的影响.