关于高中数学教学中函数和数列相结合的解题分析

姚蔚

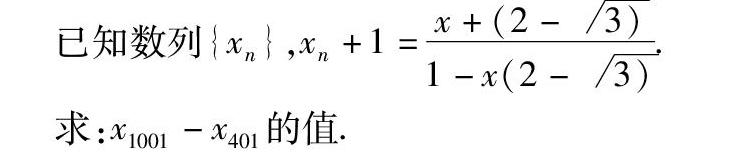
【摘要】高中数学各个知识点之间具有必然的联系性，为帮助学生分析数列问题，需要运用函数思想，因此，将函数与数列相结合是高中数学教学的主要策略.

【关键词】高中数学；函数和数列相结合；解题思路分析

一、高中数学中函数和数列知识的联系

从数列概念说，数列是一种特殊的函数，将其按照一定顺序排列，函数被定义域为有限子集，如果按照定义理解的话，将函数自变量按照从小到大顺序排列，就会得到相对应的数列数值.数列通项求和公式就是函数特性的对应意义，同时具有函数固有特征.所以在解决高中数学中数列问题的过程中，需要及时利用函数知识来进行解题，并将数列的图像和固有特征作为一座桥梁，从而及时揭示高中数学中函数和数列之间的关系[1].当学生刚接触数列知识时，自身的知识结构还处于完善时期，因此，在解决数列问题时需要引入函数思想，将函数与数列及时结合起来，同时教师要及时给予学生引导，从而帮助学生明确函数与数列的关系，在此次解题过程中，函数与数列相结合的解题思路给高中生留下了深刻印象.

二、高中数学中函数与数列相结合的解题思路分析

数列是函数的另一种形式，因此，可以依据函数来解析数列，函数与数列相交时的点成为一组数列.在进行函数与数列解题时必须要熟练掌握数列通项公式以及公式与函数的关系，对其进行正确理解.及时找到关键点，在数列计算的过程中，可以利用函数图像来分析通项公式与求和公式，套用函数来进行数列解题.

（一）解题过程

题目：等差数列{an}前n项和sn=m，前m项和sm=n（m≠n），以此来求出前m+n项和sm+n.

在解答以上题目时，需要及时运用到函数，并在掌握等差数列的前n项和sn性质的基础上，利用函数图像得出（0，0）点是二次函数.解答方法如下所示：

sn=An2+Bn（n∈N），

那么：Am2+Bm=n，An2+Bn=m.

公式1-公式2得出：A（m2-n2）+B（m-n）=n-m.

由于m≠n，因此，A（m+n）+B=-1，

由此得出：A（m+n）2+B（m+n）=-（m+n）.

最终得出：可以Sm+n=-（m+n）.

从以上解题中看出，在等差数列求和过程中需要运用二次函数思想.

通过对等差数列知识的研究发现了：等差数列通项公式中an=a1+（n-1）×d，an=dn+（a1-d）.在此公式中，如果p=d，且q=a1-d，得出：an=pn+q.其中的p和q都是常数，所以当p≠0时，an就是关于n的一次函数，同时得出（n，an）在y=px+q这个一次函数的图像上.

（二）借助函数与数列知识的关系解题

在进行等差数列解题的过程中需要及时运用函数与数列知识之间的内在关系来进行正确解题.

以联想法来进行解题：在解答数列有关数学问题时，教师引导学生以联想和类比的方式来将其进行转化，将一些不规则的问题用函数与数列之间的内在关系来进行有效解答，在此过程中，学生的创新思路和探索意识都得到了很大的提升.例题如下所示：

已知数列{xn}，xn+1=x+（2-3）1-x（2-3）.

求：x1001-x401的值.

（三）利用函数性质来进行数列转化

函数特征是函数性质的主要反映，因此，对函数性质进行深入挖掘可以有效简化数列解题过程，从而得到了最佳的解题效果.现如今函数的周期性和单调性在数列解题中已经得到了广泛应用，因此，教师要引导学生及时对函数进行挖掘，从而进一步巩固函数性质，并能够促进学生数列问题分析能力和解决实际问题能力的进一步提升[2].

（四）全面掌握通项公式

通项公式作为高考中有关数列式的考核难点，在对数列进行求和的环节需要不断创新思路，将数列求和分为这几种形式：

错位相减法：它是数列求和中常见的解题方法，这种方法适用于数列前n项和求和过程中.利用等比数列以及等差数列来相乘求和，及时运用错位相减法来进行求和.根据等比数列公式得出最终的表达式.错位相减法适合用在数列中前n项求和中，但是在课堂上，教师还需要对学生进行及时引导，在教师正确引导的基础上，学生找到了规律，从而可以快速、正确地解决这一难题，这对学生今后发展起到了非常关键的促进作用.

合并求和法：在数列题型中，学生在遇到一些特殊题型后就不知所措，根据这一情况，教师要引导学生积极探索数列解题的规律，将数列中的项进行有效整合，从而得到特殊性质中的各项的和，顺利地解决了这个问题，并掌握了合并求和法的应用技巧.

利用数列模型进行解题：依据数列题目来构建数列模型，在同一数列模型中建立了一个数学解题模型，有效创新了解题思路，帮助学生掌握了举一反三的能力.

三、结束语

如上所述，数列和函数都是高中数学知识的主要部分，同时这两者之间具有内在联系，因此，在实际解题环节需要将函数和数列有效结合，并加强对函数和数列知识点的科学分析，找到切入点，充分利用函数来进行数列解题.

【参考文献】

[1]胡学伶.变式教学在高中数学教学中的应用——以數列通项公式教学为例[J].新课程学习：中，2014（9）：97.

[2]吴雅琴.高中数学数列问题高考题型及解题方法研究[J].中学数学，2017（19）：87-88.