借题发挥增进探究———“比例的基本性质”观课反思

◇常立钢

教学片段：

师：在比例2.4∶1.6=60∶40 里，2.4 和 40 是比例的外项，1.6和60是比例的内项。如果把这个比例写成分数形式，该怎么写呢？

（学生展示，如图1和图2）

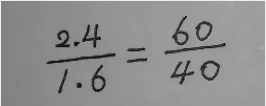
图1

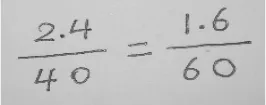
图2

生1：第一种正确（如图 1）。

师：对啊，大家看第二种写法（如图2），两个比的比值还相等吗？还能组成比例吗？

生：不能。

师：（指图1）接下来，请同学们分别将这个比例的两个外项和两个内项相加、相减、相乘和相除，看看你有什么发现。

生：两个外项相乘等于两个内项相乘。

师：是吗？还有谁有这样的发现？看来同学们都发现了在这个比例里，两个外项的积等于两个内项的积。

师：我们再换一个比例试试！噢，还存在这种关系！你能举一个例子来验证我们的发现吗？同桌两个人互相说一说。

在此基础上，老师出示：在比例里，两个外项的积等于两个内项的积。这叫作比例的基本性质。

思考：在上面比例的基本性质的教学中，老师担心直接让学生计算两个外项和两个内项的积，会有“牵引”的嫌疑，因此，引导学生分别将两个外项和两个内项进行了加、减、乘、除，以彰显学生的探究过程，拉长比例的基本性质的学习过程。实际课堂效果是，学生仍然在被动地计算，现场气氛沉闷，还有不少学生不清楚要计算什么。

那么，该如何增进学生学习中的探究性呢？在让学生将比例写成分数形式时，一个学生误写了一个比例，有学生说“2.4和1.6的位置不要乱动”，此时，如果能借题发挥，应该会增强探究性，拉长概念学习的过程。

重新设计：

师：如果把比例2.4∶1.6=60∶40 写成分数形式，该怎么写呢？

（学生展示，如图1和图2）

师：这个同学说的好像有道理，你看，2.4应该比1.6，可是第二种写成了2.4∶40，结果错了吧。可是，我偏偏想让2.4和1.6的位置动一动，（出示：）可以吗？

生：可以，两个比的比值相等。

师：位置还可以再动吗？

师：对啊，位置动了动，照样可以组成比例，这是为什么呢？在这些变化之中，好像存在不变的关系，下面请同学们分别将这个比例的两个外项和两个内项相加、相减、相乘和相除，看看你有什么发现。

……

师：学完比例的基本性质，你知道原因了吗？

生：明白了，不管怎样变，2.4和40仍然是外项，1.6和60仍然是内项，只要保证两个外项的积等于两个内项的积就行。

师：很好，下课以后，请同学们研究一下，看看这个比例可以写出多少种不同的形式。