中柱失效下多层框架的连续性倒塌分析与机理研究

乔惠云， 杨应华， 钟炜辉

(西安建筑科技大学 土木工程学院，西安 710055)

连续性倒塌是指初始局部构件的破坏向其它构件扩展，最终导致结构的整体破坏或者大范围区域的倒塌。爆炸、火灾和地震等多种原因都可能引起建筑物倒塌，倒塌破坏分析涉及到复杂的材料与几何非线性。

研究中柱失效下的抗连续倒塌，常选取梁柱子结构为框架结构的简化模型，分析其抗倒塌机制(例如梁机制和悬链线机制)。王伟等[1-2]以方钢管柱-H形梁子结构为研究对象，通过静力加载试验研究梁柱节点在中柱失效下的力学性能。史艳莉等[3]研究了圆钢管混凝土柱-H钢梁内隔板式节点抗连续倒塌工作机理。霍静思等[4]对梁柱子结构试件，采用落锤冲击的加载方法模拟结构的动态倒塌过程。杨波等[5]以H形梁柱子结构为研究对象，分析不同节点的破坏模式以及悬链线发展情况。钟炜辉等[6]以一组不同刚度的梁柱子结构为试验对象，分析结点刚度对抗倒塌性能的影响。李易等[7]基于能量方法研究了混凝土框架结构的梁机制，分析子结构的倒塌抗力需求。Izzuddin等[8]把框架结构简化为单层梁等不同的计算层次，Stylianidis等[9]推导了单层梁从开始加载到进入悬链线阶段后的简化模型，并直接把单层的特性推广到整个失效跨。

梁柱子结构模型受力简单，且容易用试验方式验证，但是目前的简化模型忽略了框架结构的整体受力特点。易伟建等[10]采用试验方式模拟三层四跨钢筋混凝土平面框架的中柱破坏，对轴力分析时提到“中柱两侧一层框架梁中产生轴向拉力，顶层框架梁中产生轴向压力”。谢甫哲等[11]采用试验研究三层钢框架在中柱拆除后的动力性能，也发现破坏跨的底部梁产生最大轴向力，而顶层轴向力为压力。李国强等[12]采用冲击去柱法对两个平面钢框架进行抗连续性倒塌试验研究。喻君等[13]指出失效柱上方各层梁的荷载传递机制不同。说明中柱失效后，多层框架结构整体受力导致各层梁的内力不相同，表现出空腹机制的特性。Sagiroglu等[14]对某七层钢筋混凝土结构模拟单柱拆除工况，得出空腹效应对抗连续倒塌有一定贡献。何庆峰等[15]模拟了单层和三层钢筋混凝土框架在冲击荷载作用下的抗倒塌性能，指出由于空腹作用，三层框架承载能力高于单层框架结构。以往对空腹机制的研究仅局限在定性分析，缺乏定量的描述。

本文首先对单层框架结构，提出梁机制和悬链线机制的抗力计算方法，得到结构的抗力-位移曲线，并通过算例验证所提方法的正确性；为研究空腹机制对多层框架结构整体受力特性的影响，建立顶层梁柱模型，计算空腹机制对框架结构抵抗连续倒塌的贡献；最后以俄亥俄州立大学综合大楼拆除四根柱的过程为例，研究空腹机制与其它机制对抵抗连续倒塌的贡献，以及各种机制下框架结构的内力分布规律。

1 单层框架结构的抗连续倒塌机制

1.1 简化模型

单层框架结构在中柱失效后，变形主要集中在与中柱相邻的两跨。研究单层框架结构抗连续倒塌机制常采用两跨梁模型[16]为子结构，如图1所示，w为柱失效点处的挠度，P为子结构的抗力。假定采用理想弹塑性本构关系，节点具有足够的强度和延性。

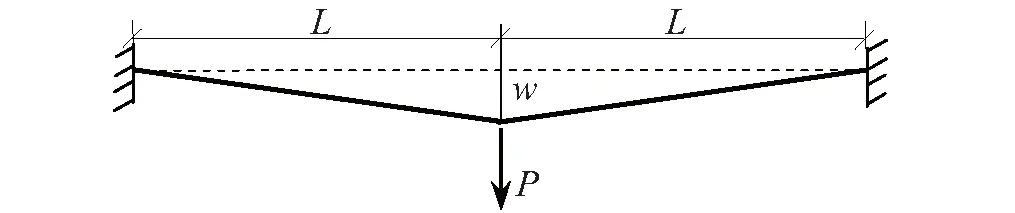
图1 两跨梁模型Fig.1 Modelling of double-span beam

1.2 抗连续倒塌机制

1.2.1 梁机制

梁机制是节点刚度较大和受剪性能较好时子结构的一种整体弯曲效应。当中柱失效后，刚性节点的弯矩充分发展从而有效地减小位移，形成主要以弯矩抵抗外荷载的抗倒塌机制。中柱失效下梁机制伴随着压拱机制[17]，本文偏于保守的不考虑压拱的作用，认为小变形下梁中轴力基本不发展，忽略梁端轴向约束。

梁端转角与柱失效点处的挠度w在加载初期较小，子结构的抗力PB1和挠度w呈线弹性关系

PB1=kew

(1)

ke=24EI/L3

(2)

式中：L为单跨梁的跨度；EI为梁截面抗弯刚度。

线弹性反应的发展程度取决于梁截面塑性极限弯矩Mp的大小，为简化分析，假设梁两端的截面同时达到Mp，经过一段时间的发展，梁的两端形成塑性铰后梁机制失效。取两跨梁模型的一半研究受力和变形，如图2所示，根据内力平衡条件，得到子结构在塑性铰形成过程中的抗力需求PB2为

PB2=4Mp/L

(3)

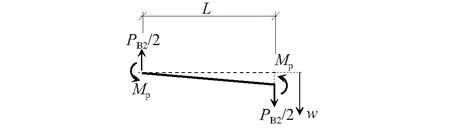
图2 塑性铰形成后的受力和变形Fig.2 Force and deformation after plastic hinge formation

在忽略轴向约束的情况下， Izzuddin[18]认为柱失效点处的挠度w等于塑性半径rp时，梁的两端形成塑性铰，塑性半径rp被定义为

rp=Mp/Fp

(4)

式中：Fp表示梁截面塑性极限轴力。对于工字型截面，rp约为截面高度的一半。

子结构在梁机制下的抗力需求可由图3所示的P-w曲线来表达。基于能量平衡原理，曲线下所包络的面积即为抗力所做的功。

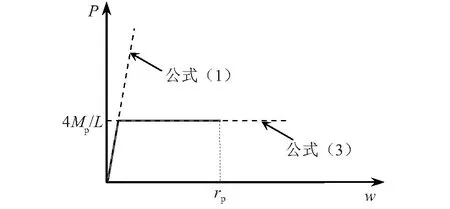
图3 梁机制下子结构的抗力需求Fig.3 Resistance demands of substructure under beam mechanism

1.2.2 悬链线机制

悬链线机制是当两跨梁模型产生大挠度变形时以拉力抵抗外荷载的一种机制，是结构抵抗连续性倒塌的最后一道防线。

塑性铰形成后，梁主要依靠轴拉力抵抗外荷载，最终截面轴力接近塑性极限轴力，截面上的弯矩减小并趋近于零。为简化分析，抗力计算先忽略梁内弯曲变形的贡献，仅考虑轴力的贡献，取图4(a)所示计算模型，随后再叠加弯矩的作用。

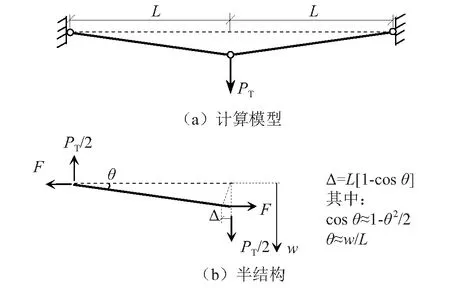
图4 悬链线机制模型Fig.4 Modelling of catenary mechanism

假设梁的轴力作用在梁截面的中心，梁的轴向受力和变形如图4(b)半结构所示，梁的轴向变形Δ取梁端转角θ的二阶近似，表示为

(5)

若梁的轴向刚度ka=EA/L， 梁的轴力F可以表示为

F=kaΔ

(6)

由图4(b)的内力平衡条件并考虑式(5)和式(6)，得到不考虑弯矩作用时子结构抗力需求PT1

(7)

塑性铰处的截面弯矩经历一段时间发展，从最大值降低到接近于零，对子结构抗力需求也有一定贡献。式(7)只考虑轴力的贡献，需要对其修正。悬链线机制在梁机制的基础上发生，所以将其起点定为梁机制结束点(rp，4Mp/L)，考虑弯矩作用后将式(7)重新表达为

(8)

梁内轴力F达到极限轴力Fp后不再增加，子结构完全依靠轴力抵抗不平衡荷载。将式(7)中轴力F用Fp代替，得到悬链线机制最后阶段的抗力需求PT2为

PT2=2Fpw/L

(9)

子结构在悬链线机制下的抗力需求可由图5所示的P-w曲线来表达。

1.3 算例分析

为检验上述理论计算的合理性，采用有限元软件ABAQUS中梁单元B22建模，使用理想弹塑性本构模型，在柱失效点处通过位移加载方式完成Pushdown分析。梁的跨度L=7.35 m，截面取H500×200×10×18 mm，分析子结构的梁端弯矩M、轴力F和抗力P随失效点处位移w变化的情况，并对比不同倒塌机制提供的抗力占总抗力的比率a，图6、7、8给出了部分计算结果。

由图6中弯矩与轴力的变化情况可知，子结构通过梁机制以及悬链线机制抵抗外荷载。由图7可知，最终梁机制完全转化为悬链线机制。此外，分别按式(1)，(3)，(8)，(9)计算得到的抗力变化曲线如图8所示，与有限元计算的结果吻合较好。

图7 不同机制的抗力比率曲线Fig.7 Curve of resistance ratio under different mechanisms

分析图6、7、8中曲线的变化，可将子结构的抗连续倒塌过程分为以下4个阶段：①当w<70 mm时，子结构由梁机制抵抗连续倒塌，抗力与位移呈线性关系；②当70 mm≤w<250 mm时，梁机制抵抗连续倒塌发挥到最大作用，梁端弯矩达到极限承载力Mp； ③当250 mm≤w<800 mm时，梁机制向悬链线机制过渡，w=600 mm时，两种机制的贡献各占一半；④当w≥800 mm时，子结构由悬链线机制抵抗连续倒塌，梁截面轴力达到极限承载力Fp，抗力与位移呈线性关系。

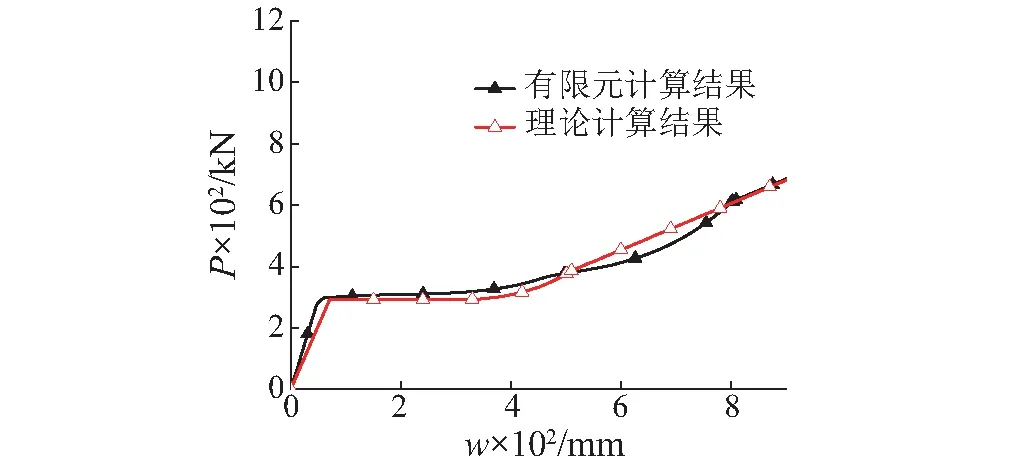
图8 子结构抗力变化曲线Fig.8 Curve of resistance for substructure

结果表明，文中提出的双跨梁模型的抗连续倒塌机制与相应机制下抗力需求的计算方法可行。

2 多层框架结构的抗连续倒塌机制

多层框架结构中柱失效后，剩余结构作为一个整体共同变形，变形主要集中在失效柱上方的两跨(失效跨)，而相邻跨的变形很小，将其作为失效跨的边界条件。由于失效跨各层的梁端边界条件不同，各层梁的轴力表现出不同的特性，顶层梁中轴力为压力，底层梁中的轴力为拉力，中间层的轴力介于两者之间。由于底层的梁端约束最强，抗力机制随变形增大由梁机制转变为悬链线机制，将底层简化为图9(a)所示的两跨梁模型。顶层的梁端约束最弱，无法形成悬链线机制，各层梁的轴力组成力偶矩与梁端弯矩一起抵抗连续倒塌，形成类似空腹桁架或空腹梁的结构，将顶层简化为图9(b)所示的顶层梁柱模型，ME为相邻构件对梁端的弯曲约束。由于顶层失效跨的轴力显著大于周边构件的轴力，简化模型忽略了周边构件对梁端的水平约束力，具体将在下文的分析中说明。

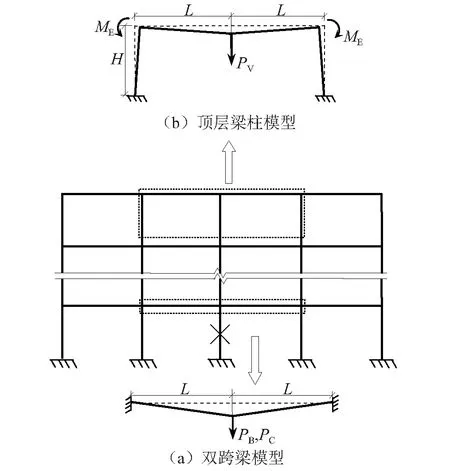
图9 多层框架在中柱失效后的子结构Fig.9 Substructure for multi-story frame under middle-column loss

2.1 空腹机制

空腹机制是多层框架结构的顶层依靠轴压力与梁截面弯矩共同抵抗连续倒塌的一种机制。空腹机制的特征主要表现在顶层的轴压力，是竖向构件对各层内力重分配的结果，体现了框架结构的整体受力特点。

假设顶层梁柱模型的节点刚度足够大，能传递与之相连构件中的所有塑性弯矩，取子结构的一半研究受力和变形，如图10所示： 跨度为L；层高为H；M、F分别表示梁端的弯矩和轴力；Mc表示柱端弯矩； 子结构的抗力需求为Pv。

由于顶层相邻跨的轴向约束不足，梁的内力不仅由失效点处的位移w确定，还由梁端的水平位移δ确定。只由w引起的梁轴向变形计算方法与两跨梁模型一样，由式(5)计算。考虑δ和w的共同作用，并由图10中δ的计算方法，梁的轴向变形Δ表示为

(10)

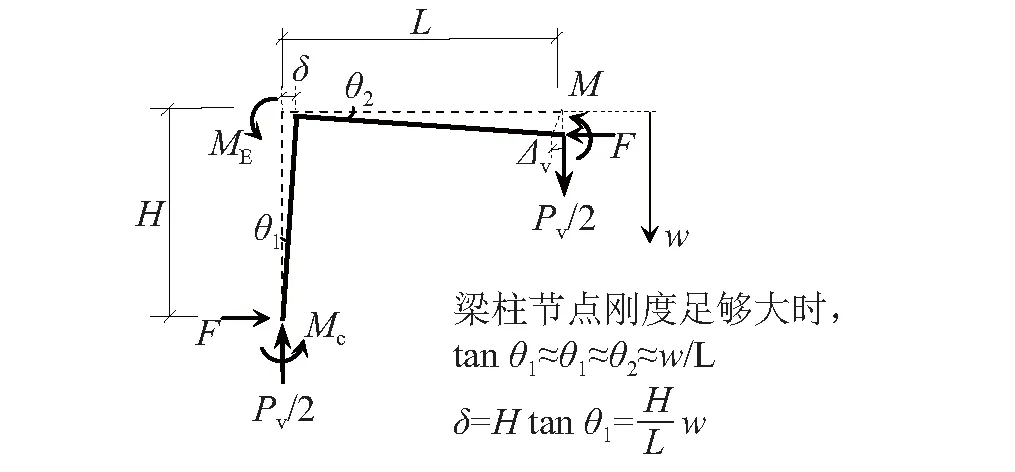
图10 顶层梁柱的受力和变形Fig.10 The force and deformation of top-story model

子结构的水平刚度kv与梁和柱的截面尺寸有关，表示为

(11)

式中：EIc为柱的抗弯刚度；EAb为梁的抗压刚度。

梁截面的轴力F为

(12)

柱失效点处位移w远小于H， 总有w-2H<0，由式(12)计算得到梁的轴力为压力。根据图10的内力平衡条件，空腹机制下子结构的抗力需求Pv为

(13)

顶层的轴压力作为空腹机制的重要特征之一，被用来衡量空腹机制对抗连续倒塌的贡献。虽然空腹机制主要表现在顶层的轴压力，但它体现了多层框架结构的整体受力特点，所以将其对抗连续倒塌的贡献分为两个层次，对顶层的贡献用指标β衡量，对剩余框架结构整体的贡献用指标γ衡量

(14)

(15)

式中：P为多层框架结构柱失效点处的抗力。

2.2 算例分析

为检验上述机制的合理性，对四层四跨平面钢框架用ABAQUS中的梁单元B22建模，跨度L为7.72 m，梁截面取H500×200×10×18 mm，层高H为4.2 m，柱截面取H350×300×20×30 mm。模型取自第3节实例的中间几跨，假设框架结构底层中柱失效，在柱失效点处通过位移加载方式完成Pushdown分析。失效点处位移最大时，剩余结构的轴力分布与变形如图11所示，失效跨各层梁从第一层到第四层的轴力分别为1 929 kN、218 kN、-51 kN、-205 kN，底层梁的轴力为拉力，最终依靠悬链线机制抵抗不平衡荷载，顶层梁为压力，表现出空腹机制的特性。

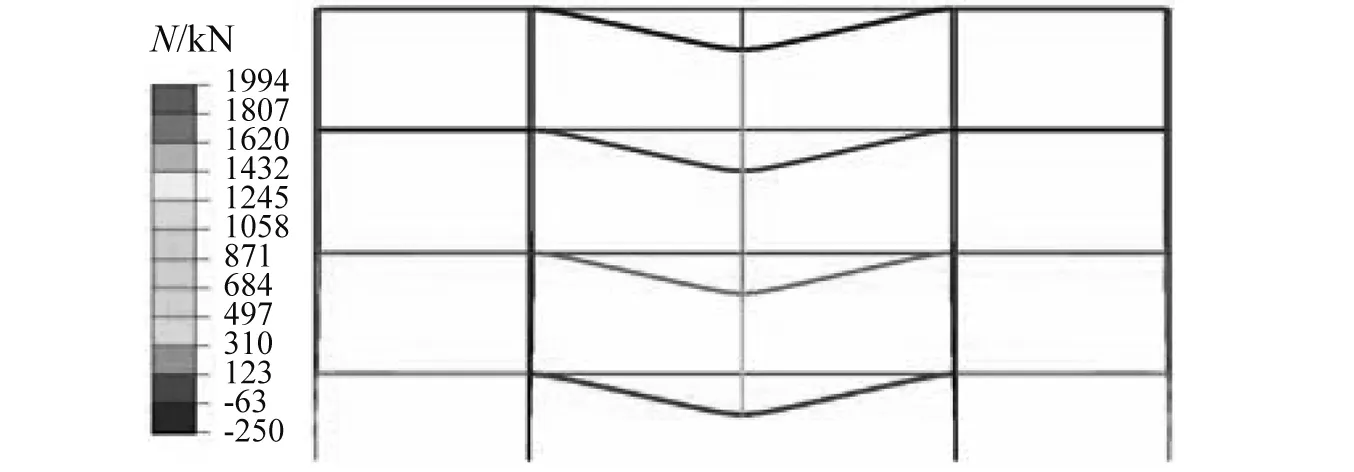
图11 剩余结构的轴力分布与变形Fig.11 Deformation and axial force distribution for remainder structure

分析失效跨梁端弯矩、轴力随柱失效点处挠度w的变化情况，并且将各层抗力P的模拟结果与理论计算结果对比，图12、13给出了顶层梁与底层梁的部分计算结果，中间层梁的计算值在底层与顶层梁之间，没有列出。

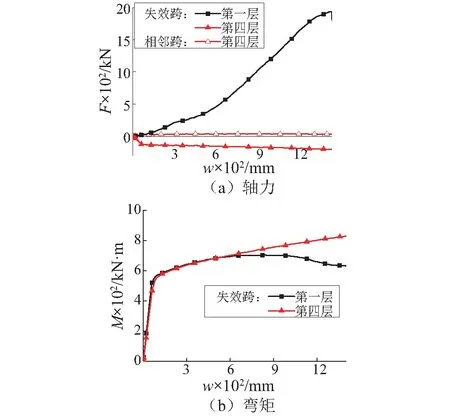
图12 简化结构内力变化曲线Fig.12 Curve of internal force for simplified structure

由图12(a)对比了失效跨与的相邻跨轴力，明显前者大于后者，特别是顶层，失效跨的轴力大小约为相邻跨的7倍，所以顶层梁柱模型忽略了相邻跨对梁端的水平约束。同时，由图12弯矩与轴力的变化情况可知，底层梁的轴力随挠度增大而增加，逐渐由梁机制向悬链线机制转变；顶层梁同时存在弯矩和压力，由梁机制和空腹机制共同抵抗不平衡荷载，建议增大顶层梁的截面尺寸，防止发生压曲破坏。此外，由图13理论计算结果与有限元计算结果对比发现，理论值略大于模拟值，这是由于在大变形时梁端的约束发生变化，但差别在3%以内。

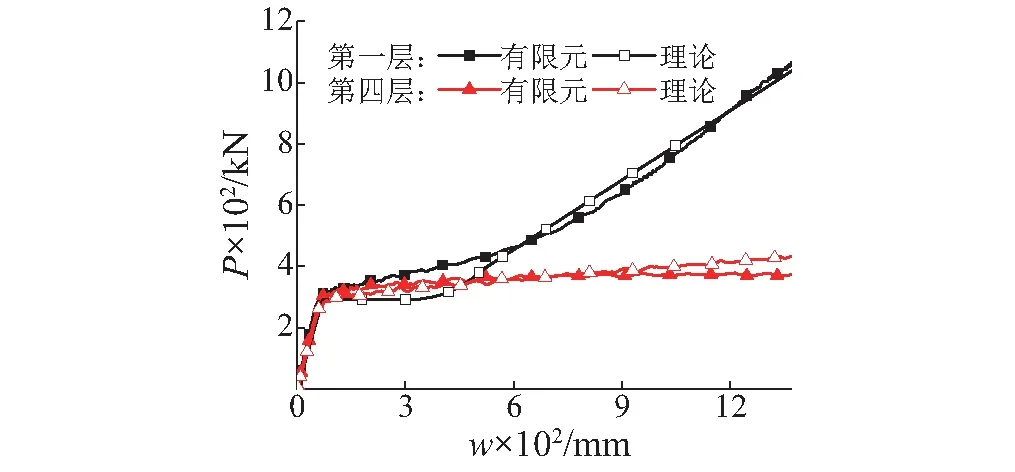
图13 剩余子结构的抗力变化曲线Fig.13 Curves of resistance for remainder substructure

顶层轴压力的贡献指标β与γ曲线见图14，由图可知，轴压力对顶层的贡献β可以达到50%左右，说明其与梁端弯矩对顶层抗倒塌有同样重要的作用。在小变形时，空腹机制对框架结构整体的抗连续倒塌贡献γ为12%左右，随着较低楼层悬链线机制的发展，贡献指标γ降低到6%。

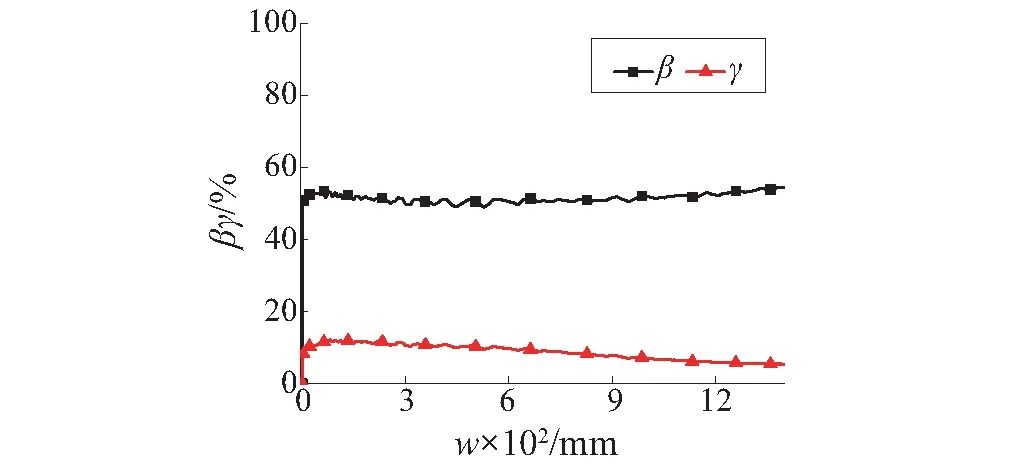
图14 轴压力对抗连续倒塌的贡献比率Fig.14 Contribution ratio of axial pressure to progressive collapse resistance

上述算例结果表明，底层梁与顶层梁表现出不同的抗倒塌机制，文中提出的多层框架抗连续倒塌机制与相应机制下抗力的计算正确可行。

3 工程实例

俄亥俄州立大学综合大楼建于1950年，采用钢框架结构，包含地上四层与地下一层，纵向8跨，横向2跨，大楼的外轮廓图与底层平面图如图15所示。文献[19]给出了结构的构件分布以及梁柱的截面尺寸。在大楼被拆除前，Song按照图15标出的顺序拆除该大楼底层的四根柱，试验人员先用切割机切除柱的底部和顶部，只留部分翼缘与主体相连，然后在短时间内用缆绳拉出两剪切面间的剩余柱段，以模拟柱瞬间失效后的结构响应，但是由于技术的限制，试验没有测到柱失效点处的位移时程曲线，原文根据其它试验数据模拟失效点处的位移，得到4根柱被拆除后，柱顶节点的最大位移分别为7.11，7.24，20.47和11.33 cm，稳定后的位移分别为6.05，6.12，17.93和9.98 cm。

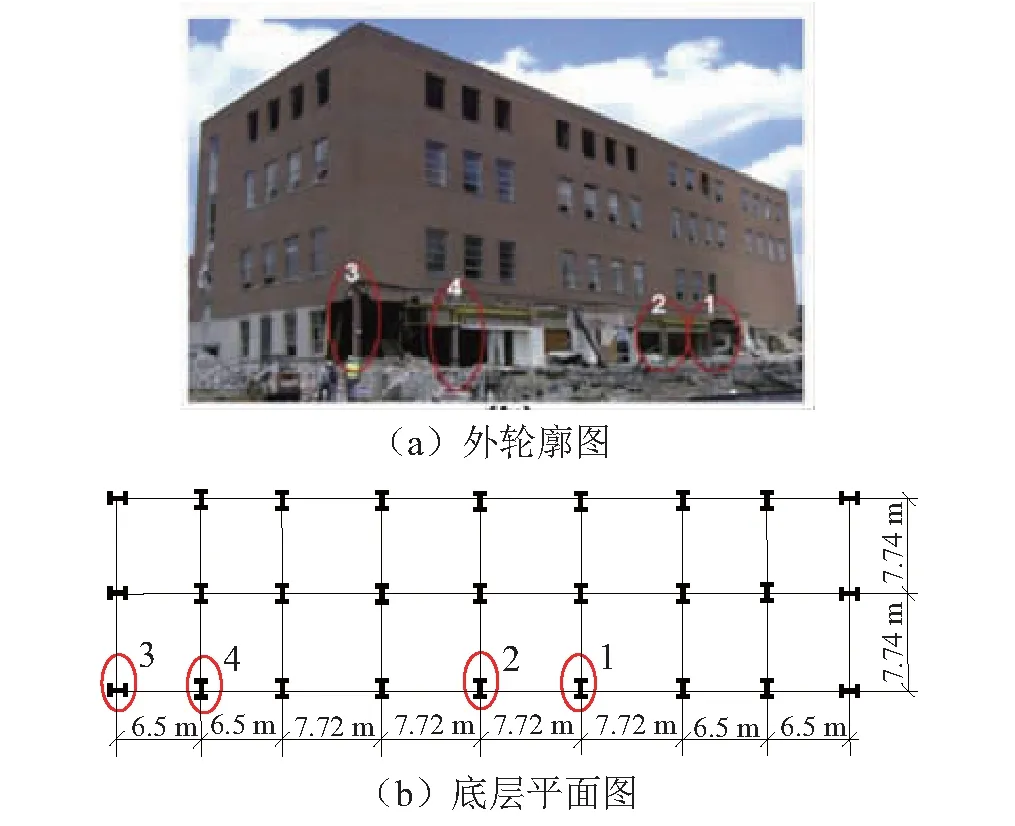
图15 俄亥俄州立大学综合大楼[19]Fig.15 The Ohio Union building [19]

采用有限元软件ABAQUS的梁单元B32建模，考虑材料与几何非线性的影响，使用理想弹塑性本构模型。拆柱时间对最后的分析结果影响很大[20]，对各柱失效后的剩余结构进行模态分析可知，第1阶竖向自振周期分别为0.38 s，0.4 s，0.4 s和0.4 s，各柱的失效时间取为0.01 s，小于剩余结构第1阶竖向自振周期的1/10[21]。模拟过程采用瑞雷阻尼，荷载组合采用1.2恒载+0.5活载。按顺序依次拆除第一到第四根柱，拆除每根柱分两步：①采用生死单元法删除失效构件；②没有动态激励，在阻尼作用下，剩余结构的动力响应逐渐趋于稳定。图16为本文模型的柱顶节点位移与文献[19]对比，稳定后四个柱顶节点的位移分别为6.33 cm，6.47 cm，17.75 cm，9.23 cm，误差在7.5%以内。此外，在四根柱相继失效的情况下，结构没有发生连续倒塌，各节点位移与跨度之比分别为1/121，1/116，1/37，1/71，抵抗连续倒塌能力较高。

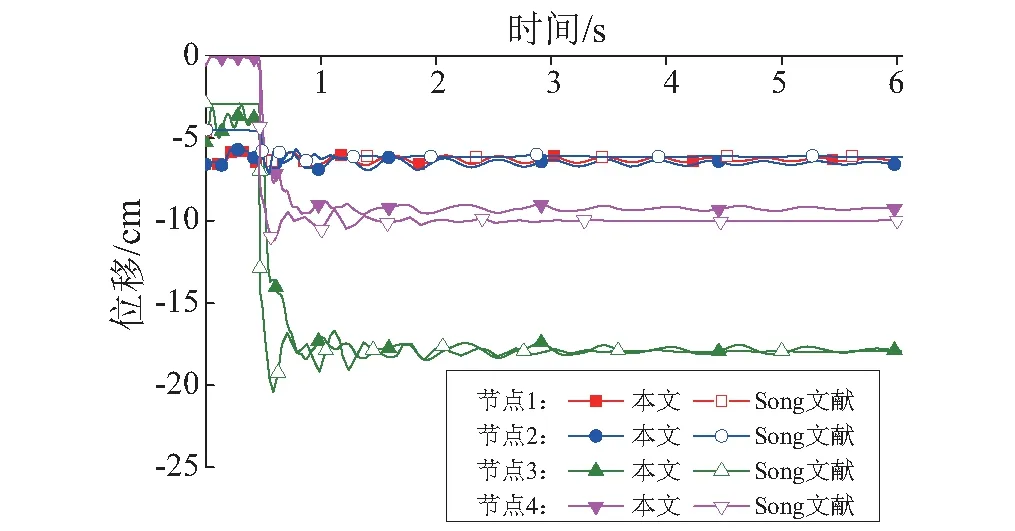
图16 本文模型与文献[19]的柱顶节点位移对比Fig.16 Comparison of displacement above each removed column between this model and references [19]

由于大楼在实验前已达到使用年限等待拆除，各种设备已被搬离大楼，使结构承受的荷载较小。以柱1和柱2的失效工况来研究框架结构中柱失效后的结构反应，在第1个位移峰值时刻，柱失效后剩余结构的弯矩、轴力情况如图17所示。

图17 结构内力分布Fig.17 Internal force distribution of structure

柱1失效后的内力分布见图17(a)所示，以柱1左侧失效跨与相邻跨的计算结果为例，

(1) 失效跨各层梁的梁端弯矩值接近，第一层到第四层分别为650 kN·m、649 kN·m、638 kN·m、597 kN·m，各层通过梁机制抵抗不平衡荷载。

(2) 失效跨各层梁的轴力值差别较大，第一层到第三层的轴力为43 kN、27 kN、40 kN；第四层的轴力为-155 kN(压力)，其对顶层的抗连续倒塌贡献系数β为47.0%，对剩余结构的贡献系数γ为14.9%，说明除了梁机制外，空腹机制也对结构的抗连续倒塌发挥作用。

(3) 相邻跨的轴力从第一层到第四层分别为11 kN、13 kN、9 kN、11 kN，顶层的轴力大小约为失效跨压力值的1/14，再结合图18相邻跨与失效跨的轴力时程曲线对比，说明顶层梁柱模型忽略相邻跨的水平约束是合理的。

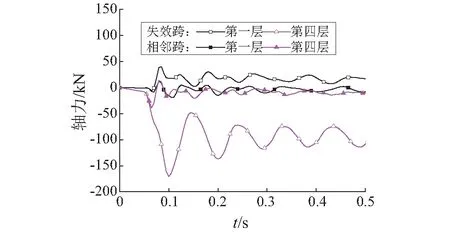
图18 柱1失效后相邻跨与失效跨的轴力对比Fig.18 Axial forces between adjacent and failure span after column 1 loss

(4) 相邻跨的右端弯矩从第一层到第四层分别为442 kN·m、393 kN·m、362 kN·m、436 kN·m，左端弯矩约为160 kN·m，显著小于失效跨梁端弯矩，再由相邻跨与失效跨的轴力对比，说明中柱失效主要影响多层框架结构的失效跨，简化模型只考虑失效跨的构件是合理的。

柱2失效后的内力分布见图17(b)所示，结构的轴力和弯矩均大幅增加，由计算结果可知：

(1) 失效跨的梁端弯矩分别为847 kN·m、830 kN·m、850 kN·m、843 kN·m，由梁机制抵抗不平衡荷载；相邻跨各层梁的梁端弯矩约为260 kN·m左右，大小相当于失效跨的1/4。

(2) 连接柱1和柱2的各层梁的轴力最大，第一层到第四层分别为201 kN、55 kN、98 kN、-409 kN(压力)；图19为柱2失效后不同跨的轴力对比，失效跨在顶层的轴力大小约为相邻跨顶层的16倍。空腹机制对顶层的抗倒塌的贡献系数β为56.7%，对剩余结构整体的贡献系数γ为19.6%。

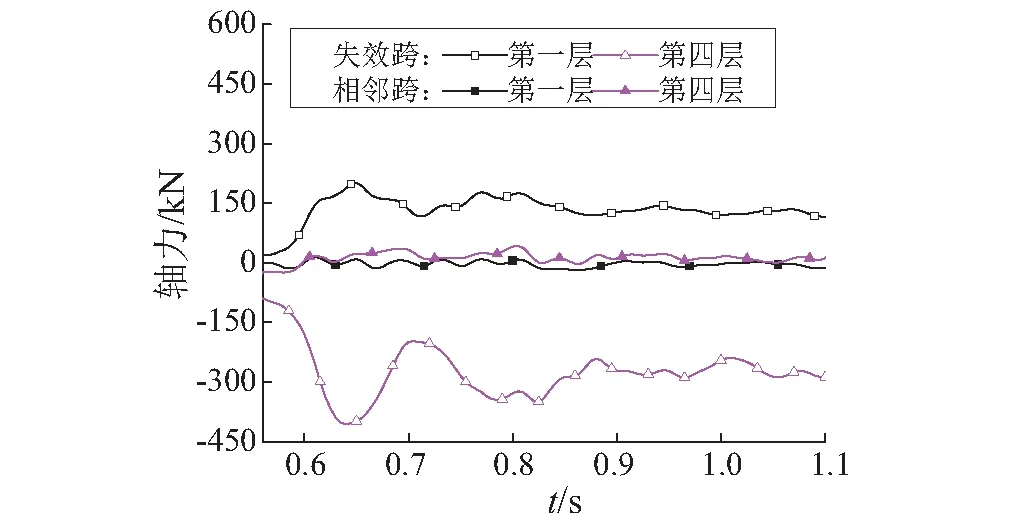
图19 柱2失效后相邻跨与失效跨的轴力对比Fig.19 Axial forces between adjacent and failure span after column 2 loss

通过上述分析可知，各抗连续倒塌机制并不单独作用，特别是顶层由梁机制与空腹机制共同抵抗不平衡荷载。

4 结 论

本文研究了多层框架结构的抗连续倒塌机制，得出主要结论：

(1) 基于两跨梁模型研究单层框架的抗倒塌机制，提出梁机制和悬链线机制的抗力计算方法，得到子结构的抗力位移曲线，并通过算例验证该方法的正确性。

(2) 为分析空腹机制对多层框架整体受力的影响，提出顶层梁柱模型，引入空腹机制对抗连续倒塌的贡献指标，并用算例验证多层框架抗连续倒塌机制与相应机制下抗力的计算正确可行。

(3) 分析俄亥俄州立大学综合大楼的抗连续倒塌机制，结果表明本文对多层框架结构简化是合理的；中柱失效后，顶层与底层表现出不同的倒塌机制，空腹机制与其它机制共同抵抗连续倒塌。

(4) 俄亥俄州立大学综合大楼在底层四根柱相继失效的工况下没有发生整体倒塌，说明该结构具有较好的抗连续倒塌性能。