机车传动系统故障特性分析
杨 柳, 李 强, 杨绍普, 王久健, 顾晓辉
(1. 北京交通大学 机械工程学院,北京 100044; 2. 石家庄铁道大学 机械工程学院,石家庄 050043)
工程中受复杂激励作用下,机车传动系统动态分析是机车运行状态和疲劳强度的关键。尤其是在机车高速运行中,出现的轴承及齿轮故障会对机车运行带来很大的安全隐患。所以如何准确建立非线性转子动态模型及检测转子的振动成为分析的关键。
机车转子系统由轮对齿轮、轴承及主、从转轴组成。最初,Jeffcott转子系统,经常被用作研究大型柔性转子结构模型,系统稳定性、临界转速和动态特性[1-3]。Jeffcott[4]最早提出并分析了转子动力学单自由度模型。并研究了在超临界运行时,转子具有自动定心现象。之后,Cveticanin[5]建立了Jeffcott 转子的二阶挠度函数的非线性微分方程,并对Jeffcott转轴进行了稳定性分析。Isahida等[6]利用Jeffcott转子模型,出现2倍转频时,分析系统非线性分岔特性及内共振现象。随着工业发展,对称转子系统轴-齿轮-轴承耦合系统分析成为研究重点[7]。转子系统的特性研究主要从Tiwari等[8]建立了考虑轴承间隙的滚动轴承-转子系统动力学模型,用数值积分的方法研究了轴承间隙对其非线性动力学响应的影响,并用Floquet理论分析了其运动稳定性。陈果等[9]建立了滚动轴承支承下的转子系统非线性动力学模型。齿轮传动系统方面: Karaman等[10]分析了直齿轮啮合间隙非线性特性。Tsuta等[11]研究了时变刚度、齿侧间隙对齿轮传动系统响应的影响。王建军等[12]提出了齿轮系统振动力学的理论体系。国内有很多学者已经对齿轮啮合刚度、动力学仿真、故障检测有了很深入的研究[13-14]。轴承动力学研究主要集中于正常轴承或整个转子的动力学行为,对于故障轴承-转子的动力学研究相对较少。现有的研究方法主要分为两大类:一类方法将滚动体滚过缺陷时数值模拟与仿真[15-16];另一类通过实验数据对加工故障进行分类与检测[17]。
以上文献研究可以看出,现有转子动力学模型大多数只是研究转子振动响应,而忽略了支撑轴承、啮合刚度等非线性因素的影响。对与考虑齿轮-转轴-轴承等复合故障因素作用下,机车传动系统动力学模型较少。本文在前人基础上,研究了机车传动系统动力学模型,考虑轴承接触及啮合刚度因素。针对轴承内、外圈和齿轮齿面磨损、齿根断裂的故障基础,准确的给出齿轮、轴承故障特征表达式。不同故障类型下,系统响应特征和相关性。本文能够很好仿真实际故障类型模型,节约实验、时间及其劳工成本,为实际结果提供理论依据。
1 动力学模型
考虑轴承、齿轮啮合刚度、驱动激励、复杂条件下的机车传动系统动力学模型,如图1所示。
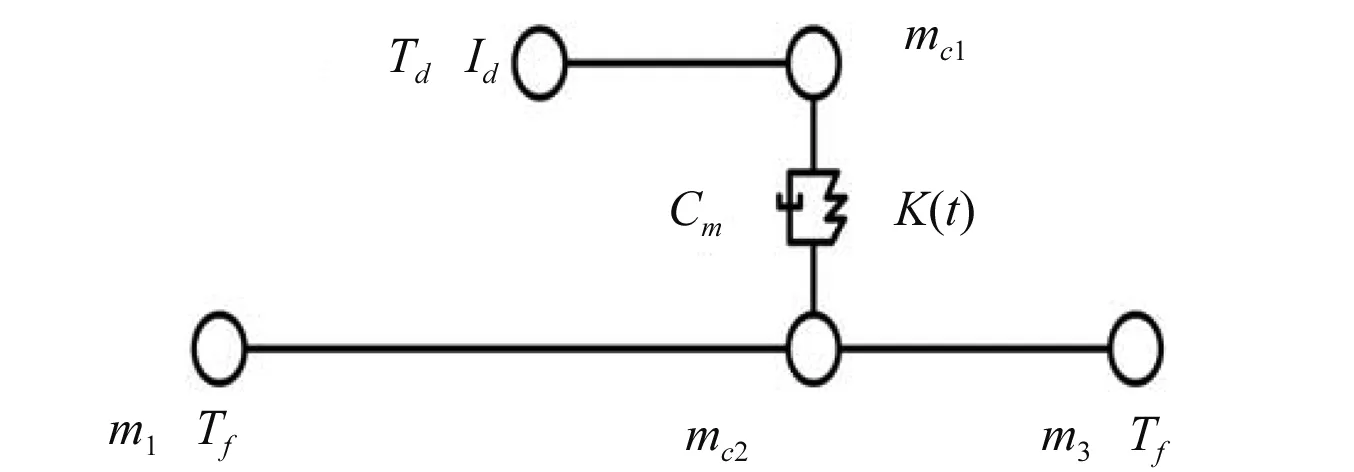
图1 机车传动系统模型Fig.1 Locomotive dual rotor model
转子系统非线性动力学模型如图1 所示, 在该模型中,假定齿轮、轴承为集中质量单元,考虑轴承支撑力及齿轮啮合刚度等参数的影响。 图中,Td转子驱动转矩,m1、m3左右支撑轴承质量,mc1、mc2主、 从动齿轮质量,Tf转子负载转矩。Cm、k(t)分别为轮齿啮合阻尼、时变刚度。
根据拉格朗日原理,轴承-齿轮-转子系统的动力学方程
输入轴:
(1)
输出轴:
(2)
式中:θd为输入扭转角;ρi为转子极坐标位移;Fm为齿轮啮合力;FN1,FN3为左右轴承赫兹接触力;Ct1、Kt1为扭转阻尼, 扭转刚度Cs11、Ks11弯曲阻尼、弯曲刚度。
1.1 齿轮时变啮合刚度
机车齿轮传动的振动形态为周期时变特性,单齿与双齿啮合交替变化。其中,齿轮啮合模型如图2所示,齿轮时变刚度可近似展开为
Km(t)=k0+km∑(aicosΩt+bisinΩt)
(3)
考虑间隙、齿轮啮合刚度作用,齿轮啮合力
Fm=Km(t)(ρc1-ρc2+θc1r1-θc2r2-e)
(4)
齿轮偏心力对齿轮系统影响
Wc=mciriΩ2eiΩt
(5)
式中:Km(t)为齿轮时变啮合刚度;r1、r2为主从动齿轮的半径;mci为啮合齿轮质量;Ici为啮合齿轮转动惯量。

图2 啮合轮齿单元模型Fig.2 Meshing tooth unit model
1.2 轴承单元模型
从动轴支撑圆锥滚子轴承由外圈、内圈、圆锥滚子和保持架构成。如图3所示的圆柱滚子轴承,忽略轴向作用力,考虑法向接触力,由非线性赫兹接触理论,可以得滚动体与滚道之间的接触力
(6)
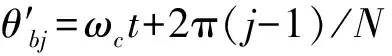
(7)
由于外圈转速为vo=0, 内圈转速vi, 保持架角速度为
(8)
式中:r为轴承转子内圈半径;R为轴承转子外圈半径。

图3 轴承接触单元模型Fig.3 Bear unit model
2 系统故障类型
齿轮破坏主要有以下集中,制造、装备及工况引起齿形误差,齿轮磨损,齿面疲劳破坏及齿根断裂。而轴承主要故障主要为:轴承内圈、轴承外圈、滚动体、保持架破坏。这里主要研究齿轮磨损及断齿破坏,及轴承内、外圈局部故障破坏工况。
2.1 齿轮磨损故障
为了能够准确给出齿轮磨损、点蚀等故障刚度特征表达式,通过准确求解齿轮刚度[18],如图(4)所示,采用Fourier级数法模拟磨损故障刚度
Kw(t)=Km(t)-∑{A0-Aisin(ωmt)}B(θ)
(9)
式中:Ai为磨损故障的幅值;B(θ)为开关控制函数
(10)
式中:zc磨损齿轮齿数;nj为齿轮磨损标记的齿数; Δθ为磨损条件齿廓与中心夹角。

图4 齿轮磨损刚度Fig.4 Gear abrasive stiffness
2.2 齿轮断齿故障
齿轮齿根破坏时,齿轮刚度如图(5)所示,齿根出现断裂时啮合刚度为零,断齿故障刚度表达式为
Ku(t)={Km(t)-Kmδ(t)}
(11)
式中:δ(t)为开关控制函数。
(12)
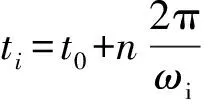
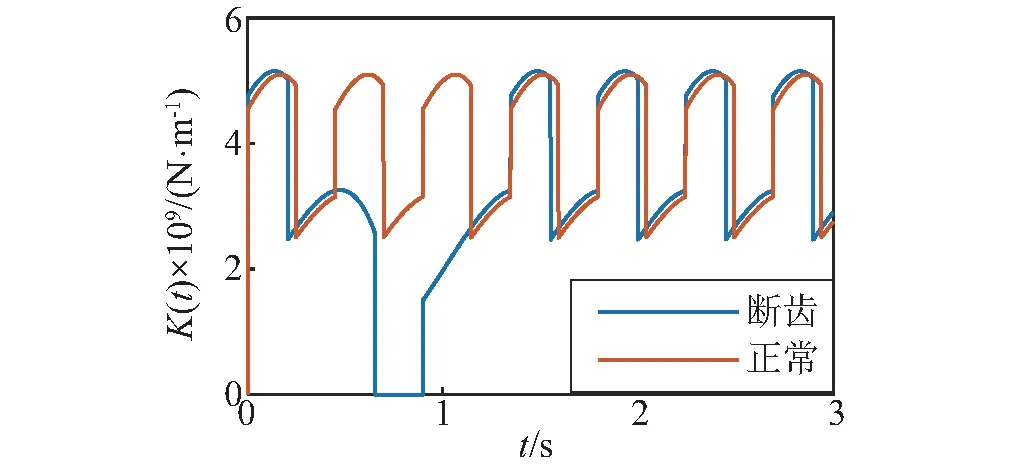
图5 齿轮断齿刚度Fig.5 Snaggletooth stiffness
2.3 轴承外圈故障
如图(6)所示,轴承外圈局部故障时,缺陷所在位置角为θd, 缺陷对应的圆心角为θo, 且损伤宽度为B。 滚动体通过该处时,会有一定的法向变形量为λ, 圆柱滚子半径为Rz, 周期内,变形量大小为
(13)
圆锥滚子在故障区域的变形量会导致非线性赫兹接触力的变化,单个圆柱滚子法向接触的变形量大小为
δo=ρeiθit-γ0-λ
(14)
式中:θi=ωct+2π(i-1)/N,N为滚子个数;γ0轴承游隙。

图6 轴承外圈故障Fig.6 Bear with an outer race defect
2.4 轴承内圈故障
如图(7)所示,轴承内圈局部故障时,缺陷所在位置角为θd1, 缺陷对应的圆心角为θi, 且损伤宽度为B1。 滚动体通过该出时,会有一定的法向变形量为λi, 圆柱滚子半径为Rz, 周期内,判定内圈与单个滚动体位置的旋转角度
(15)
式中:ωr为内圈转速;ωc为保持架转速;φ为第j个滚珠的初始角;θc=mod(ωst,2π)。
变形量大小为
(16)
圆锥滚子在故障区域的变形量会导致非线性赫兹接触力的变化,单个圆柱滚子法向接触的变形量大小为
δi=ρeiθj t-γ0-λi
(17)
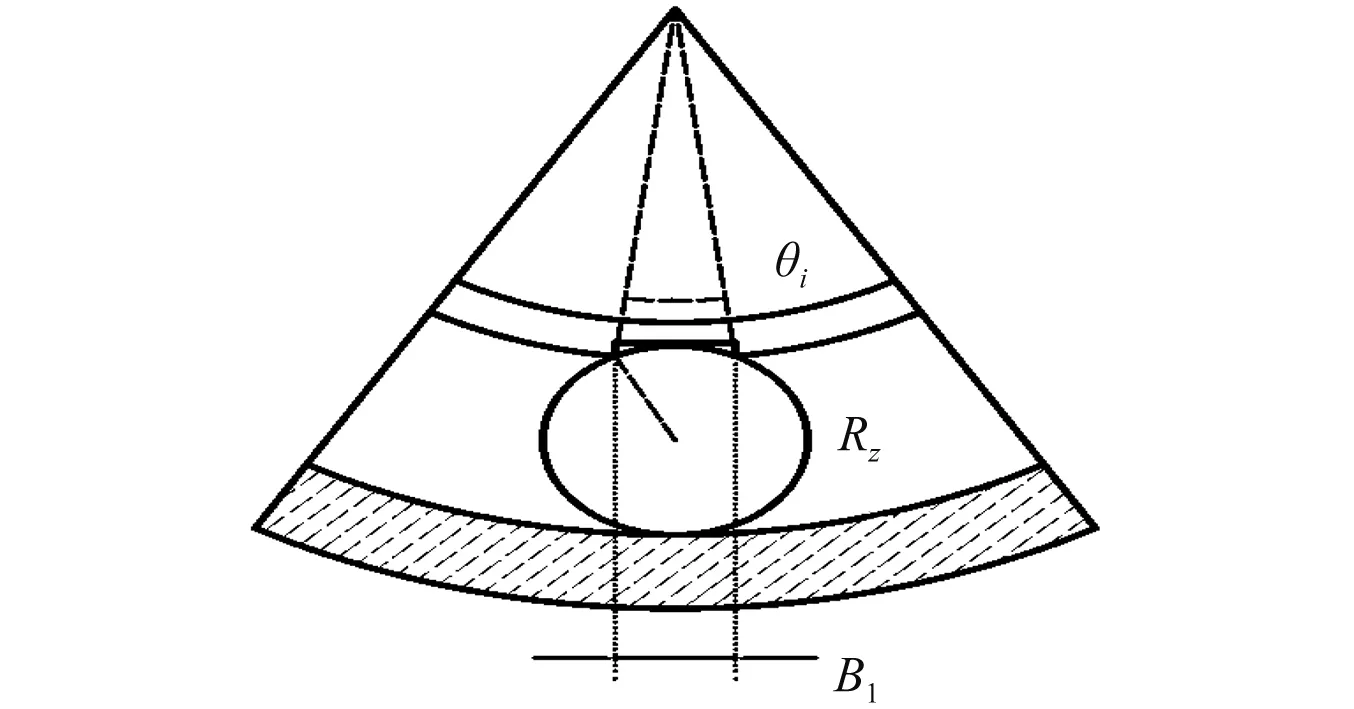
图7 轴承内圈故障Fig.7 Bear with an inner race defect
轴承内圈或外圈故障时, 法向Herz接触应力为
(18)
3 系统信号仿真及分析
本文根据CRH系列机车作为研究对象,机车系统参数为: 支撑轴系长度为L=2 100 mm, 轴截面外径为R=200 mm, 内径为r=65 mm, 集中惯性质量为Id=18.75 kg·m2; 啮合齿轮质量mc1=20 kg;mc2=120 kg; 齿轮模数为ma=6 mm, 齿数为z1=14,z2=63, 齿轮时变啮合刚度Km, 支撑轴承NJ2232,滚子个数N=17,ri,ro为轴承内、外圈半径, 主动轴运行转速n1=800 r/min;D轴承节径;d滚动体直径。
特征参数值:
齿轮啮合频率:fm=f1z1=f2z2,
研究正常齿轮、轴承状态下机车传动系统动态响应。如图8所示,在时域响应中,系统响应混叠性较强,没有明显的周期冲击特性。从图8所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量。轴承信号能量较小,在低频带中未发现轴承通过频率vc,而在齿轮啮合频带处,有非对称的边频现象。

图8 正常系统响应Fig.8 Time-frequency Analysis
3.1 故障齿轮
主动轴齿轮齿面出现轻微磨损,其它正常。如图9所示,在时域响应中,系统呈稳态变化过程,图中T1为磨损齿轮轴转动周期。从图9所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量,其中,齿轮磨损时,频谱图中啮合频带有明显的非对称式边频现象,这主要受到磨损量在齿面的分布影响。轴承信号能量较小,在频带中未发现轴承通过频率vc。
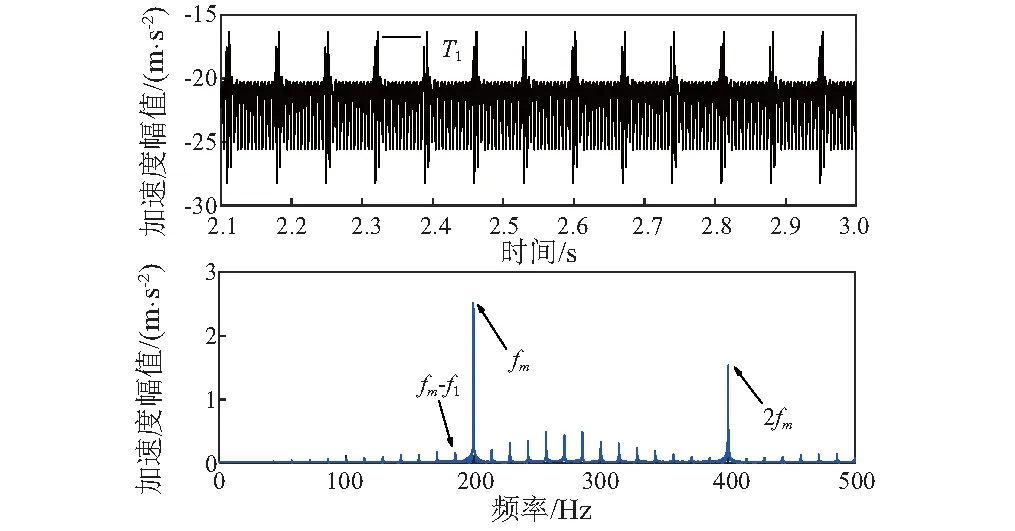
图9 齿轮磨损-系统响应Fig.9 Time-frequency Analysis
主动轴齿轮出现齿根断裂,轴承正常。如图10所示,时域响应中,系统呈单边衰减过程,T1为断齿齿轮轴转动周期。 从图10所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量,其中,齿轮断齿时,频谱图中,啮合频带有明显的边频现象,且会激起固有特征频率fn处引起系统共振特性。 轴承信号能量较小, 在频带中未发现轴承通过频率vc。
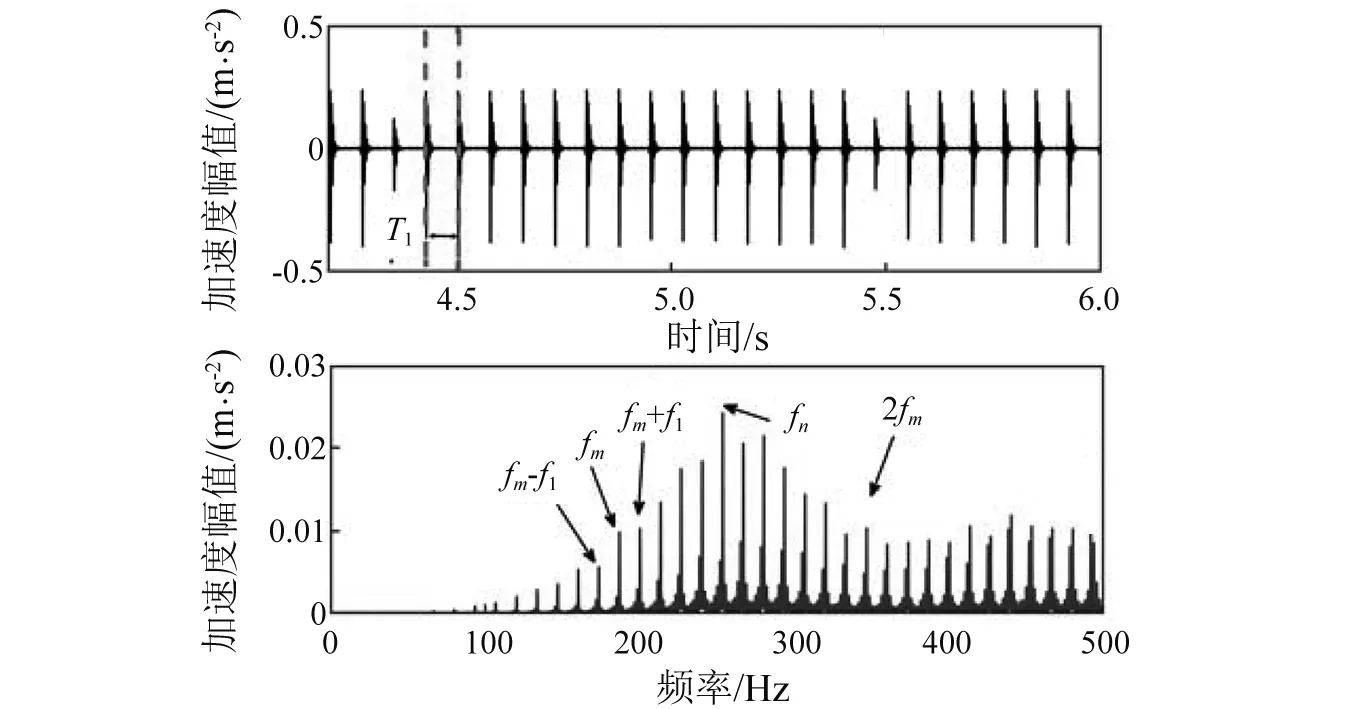
图10 齿根断裂-系统响应Fig.10 Time-frequency Analysis
3.2 故障轴承
从动轴轴承外圈局部局部故障,齿轮正常。如图11所示,时域响应中,系统呈周期脉冲响应,To为轴承外圈故障特征周期。从图11所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量。 轴承故障时,频谱图中,外圈故障频率周期激励下,啮合频带有明显的边频特性,在低频带中有微弱的轴承外圈故障频率fo。

图11 轴承外圈-系统响应Fig.11 Time-frequency Analysis
从动轴轴承内圈局部故障,齿轮正常。如图12所示,时域响应中,系统呈周期响应,Ti为轴承内圈故障特征周期。从图12所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量。轴承故障时,频谱图中,啮合频带有明显的边频特性,在低频带中有微弱的轴承内圈故障频率fi。
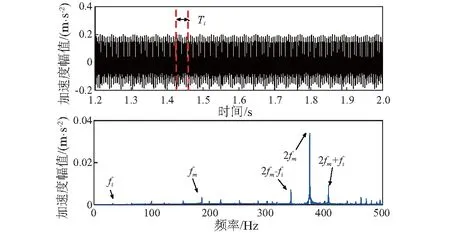
图12 轴承内圈-系统响应Fig.12 Time-frequency Analysis
3.3 系统复合故障信号的相关性及能量准则
研究齿面出现磨损,轴承出现内圈故障时,系统的振动响应。如图13所示,在时域响应中,系统响应混叠性较强,但有明显的齿面磨损转轴周期特性。从图13所示的频谱中,可清楚地找到啮合频率fm及其倍频2fm对应的分量,由于齿面破坏,引起啮合频带周边有明显的边频现象。而轴承信号能量,在传动系统中衰减较快,频带中未能找到轴承通过频率,而在高阶齿轮啮合频带处,有非对称的轴承内圈边频现象。

图13 复合故障-系统响应Fig.13 Time-frequency Analysis
通过轴承单元信号利用改进的EEMD[19-20]方法分析,寻找故障轴承信号分量中的最大谱峭度值,之后,与齿轮单元信号做互相关性。如图14所示,时域响应中,系统响应有明显的轴承冲击特性。从图15所示的频谱中,可清楚地找到啮合频率fm及其倍频对应的分量。在齿轮啮合频带处,有明显的轴承内圈故障引起的边频现象。频谱中也清晰地发现,通过求取互相关信号函数下,齿轮破坏下的轴频特性减弱。

图14 轴承单元频谱响应Fig.14 Bear frequency

图15 轴承单元时域响应Fig.15 Bear tines response
6 结 论
本文建立了转子传动系统弯扭耦合动力学模型,考虑了非线性齿轮啮合刚度及轴承接触的影响。研究了轴承、齿轮单元的故障特征。
(1) 建立了传动系统转子模型,能更好的分析轴、齿轮之间的相互传递关系及影响。
(2) 齿轮、轴承单元的故障表式,能够准确的表达故障类型。
(3) 不同输入故障类型下,仿真模型响应能够有效的展现各故障信号输出特征。复合故障下,轴承信号特征微弱,通过故障单元相关性,有效地提取轴承微弱故障信号特征。
总上所述,机车传动转子系统模型,不同于传统转子模型,对铁路机车传动系统动力学分析及齿轮轴承等故障分析提供了很好的动力学模型依据。

