三向压电悬臂梁振动能量采集器的研究
马骁骏, 冷永刚, 刘进军, 范胜波
(天津大学 机械工程学院, 天津 300310)
近年来,电子设备的发展已进入小型化、低功耗的时代[1-2]。电池通常作为这些设备的供能装置,存在着体积大、容量小、易损耗、常更换等缺点,因此人们需要寻找一种新的供能方式来替代电池。振动能量作为一种清洁、可持续的能源,广泛存在于自然环境中,因而如何获取振动能量并将其转换为电能已成为研究热点。压电式振动能量采集方式由于具有体积小、高能量密度等优点,获得了较多的关注[3-4]。传统线性压电振动能量采集装置由于频带较窄,因此很难适用于宽频带的振动环境。运用非线性磁铁作用力设计的非线性压电悬臂梁振动能量采集系统,可以有效扩展系统频带并采集不同环境的振动能量[5-7]。
通常传统的压电能量采集器是以单个压电悬臂梁为基础,存在只能采集空间一个方向的振动能量的缺陷。实际环境中的振动可能来自三维空间的任意方向,因此如何实现各个方向的振动能量采集,以获取更多的振动能量有着重要的研究价值和意义。针对这一问题,Fan等[8-9]于2014年提出了一种悬臂梁式的二维振动能量采集系统,实现了在性能上略优于线性压电能量采集装置,之后于2015年提出了一种磁力球式非线性悬臂梁能量采集装置,实现了扭转方向的振动能量采集。Chen等[10]提出了一种类似蒲公英结构的多维能量采集装置,能够有效地采集多方向振动,然而其结构中的悬臂梁的振动均为线性振动,难以适应实际宽频激励的能量采集,并且其结构较为复杂,难以加工;Su等[11-12]于2013年提出了一种三维方向上的振动能量采集装置,可实现三维方向能量采集,并能适应实际宽频的振动响应,然而由于其结构中采用弹簧滑块结构,易导致摩擦损耗能量,因此降低了能量采集效果,之后于2014年Su对二维方向上的悬臂梁振动能量采集进行了细致的研究和优化。
为了避免压电悬臂梁因结构间摩擦而产生的自身能量损耗,尽可能地提高能量获取效率,本文仅采用三个压电悬臂梁所组成的非线性结构,提出了一种具有同时俘获空间各个方向振动能量的采集系统,通过对该能量采集系统的动力学建模与仿真和实验分析,揭示了系统的振动响应特征和能量采集规律,为实际环境振动能量的有效采集提供了基本分析方法和技术基础。
1 三向压电梁振动能量采集结构及动力学建模
非线性三向压电悬臂梁振动能量采集系统(以下简称“三向采集系统”)的基本结构如图1所示。该结构由三个压电悬臂梁(a, b, c)和三个永磁铁(A, B, C)以及基座D组成。其中三个压电梁和三个永磁铁的形状尺寸均分别相同。悬臂梁a, b, c均由金属基体和压电陶瓷片组成。金属基体上下表面各粘贴一层压电片(PZT),两层压电陶瓷片同极化方向排列且几何尺寸相同。三个永磁铁型号均为N35。三个悬臂梁a,b,c平面两两相互垂直且自由端均分别固定有永磁铁A, B和C,其中A和C均与磁铁B相互排斥。悬臂梁a, b, c自由端的磁铁分别沿x,y,z轴方向振动。三向采集系统在初始平衡位置时,磁铁A, B, C的中心沿y轴水平对中,且三个梁均无弯曲,如图1和图2(a),为做到这一点,磁铁A, B初始平衡间距d1以及磁铁B, C初始平衡间距d2应保持相等,即d1=d2=d0,此外三向采集系统振动过程中,磁铁A、B以及磁铁B,C之间不应发生碰撞干涉。
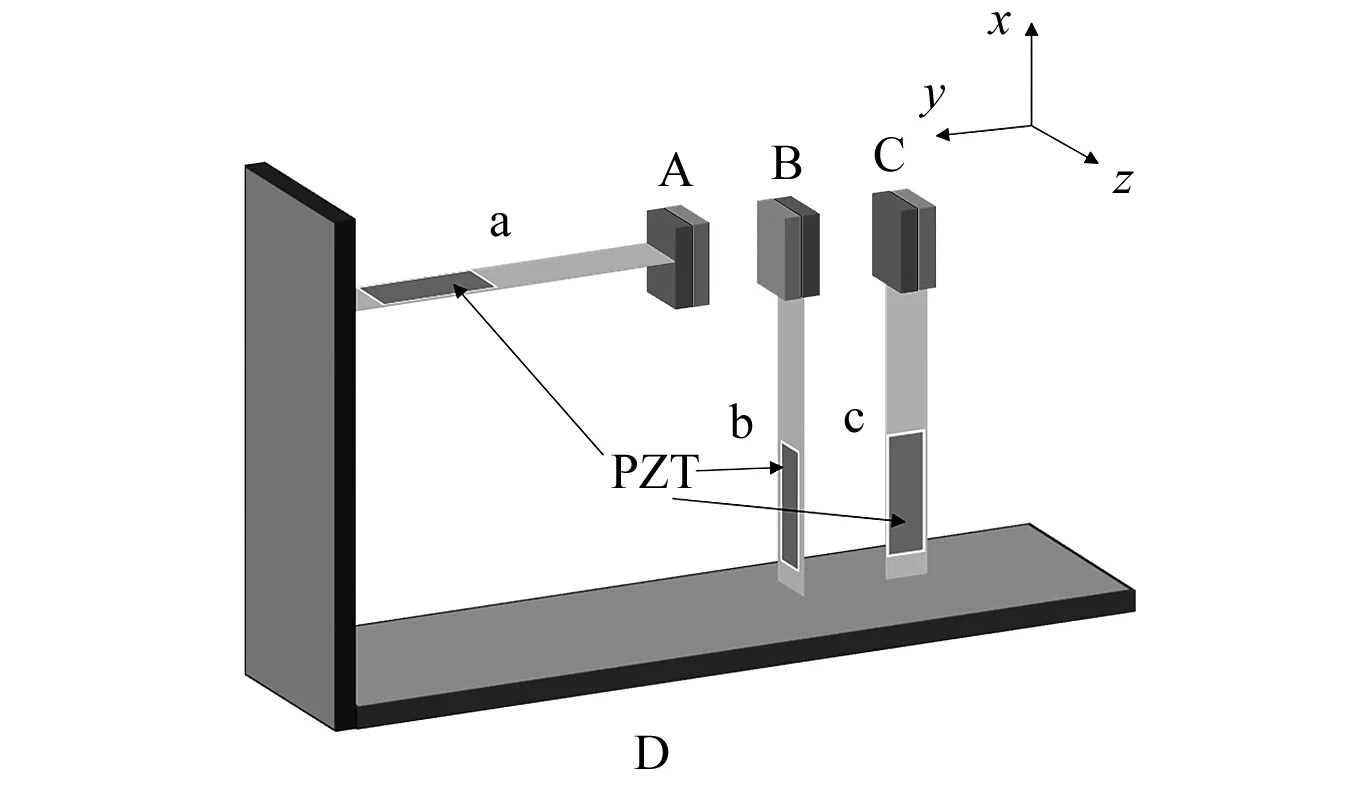
图1 三向压电悬臂梁振动能量采集系统结构示意图Fig.1 Schematic diagrams of the three-dimensional energy harvester
当基座D受到x方向的外界激励Px(t)作用时,如图2(b),悬臂梁a产生x轴方向上的振动,使得A和B两磁铁间的磁铁力发生变化,导致悬臂梁b产生沿水平y轴方向上的振动;而悬臂梁b的运动又改变了B和C两磁铁间的磁铁力,致使悬臂梁c产生在z轴方向上的振动。因此,x方向的激励可以同时引起三个梁的摆动,使得PZT压电陶瓷发生变形,产生压电效应,达到振动机械能转换为电能的目的,实现振动能量采集。同理,当激励在y或z轴方向时,也会同时引起三个悬臂梁的摆动,也可实现振动能量采集的目的。当外界激励来自任意方向时,可以将该激励分解到x,y,z三个方向上,视为系统同时受到Px(t)、Py(t)、Pz(t) 三个方向的激励作用。

(a)初始平衡状态

(b)受力分析图图2 三向采集系统的初始平衡状态和受力分析图Fig.2 The schematic diagrams of initial state and Force analysis at time t
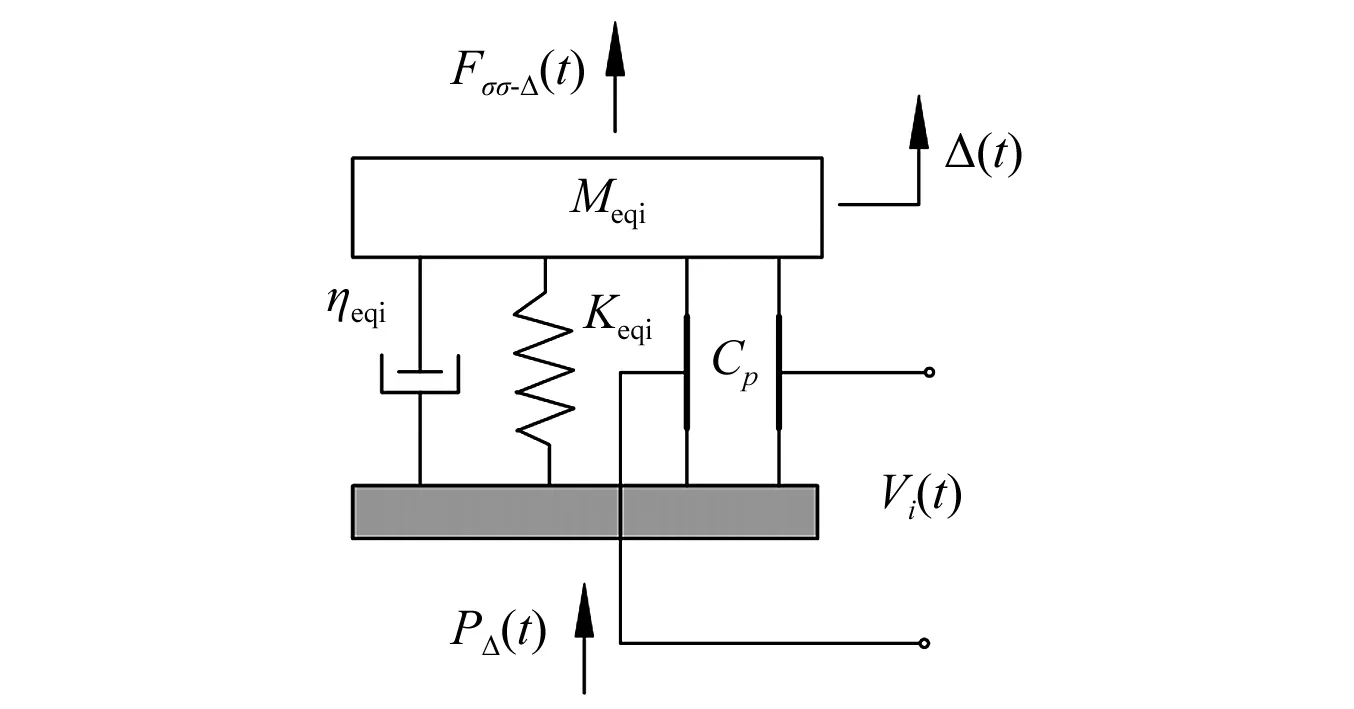
图3 每个压电悬臂梁能量采集结构的等效模型Fig.3 Equivalent model of each cantilever
根据图1结构,三向采集系统中的每一个梁均可简化成典型的质量弹簧阻尼模型,每个梁的等效模型如图3所示[6]。对于梁a,其末端磁铁受到磁铁B和C的磁铁力作用,以及x方向的激励;对于梁b,其末端磁铁受到磁铁A和C的磁铁力作用,以及y方向的激励;对于梁c,其末端磁铁受到磁铁A和B的磁铁力作用,以及z方向的激励。图中Meqi,ηeqi,Keqi分别表示悬臂梁的等效质量、等效阻尼和等效刚度,Vi(t)表示悬臂梁上压电片的输出电压,下标i取1, 2, 3分别表示悬臂梁a, b, c;PΔ(t)代表外界激励,Δ(t)表示位移,Fσσ—Δ(t)表示两磁铁间的作用力,符号Δ取x,y,z分别表示空间三个方向,σσ表示三个磁铁中的任意两磁铁;Cp为电路电容。根据牛顿第二定律,可以得出整个能量采集系统的动力学方程[6]:
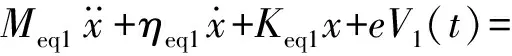
(1)

(2)

(3)
其中e为压电陶瓷PZT的机电耦合系数。根据基尔霍夫第一定律,可以得到各个压电悬臂梁的采集电路方程[13]:
(4)
式中:RL为电路外接负载电阻。
因磁铁A, B, C以及悬臂梁a, b, c均分别采用相同材料和形状尺寸,故Meq1=Meq2=Meq3=Meq,Keq1=Keq2=Keq3=Keq,ηeq1=ηeq2=ηeq3=ηeq三个梁的等效电路相同。Meq,ηeq,Keq以及e,CP等参数可由文献[6]得到。
2 非线性磁铁力分析
三向采集系统的磁铁A, B, C可先简化成三个磁偶极子,然后根据磁偶极子理论[14],分析计算悬臂梁任意振动位置的非线性磁力及其所具有的势函数。
2.1 非线性磁力
对于悬臂梁a,因为磁铁A和C之间的初始平衡位置间距相对较大,在初始状态时FAC远小于FAB,并且系统在振动过程中,磁铁A和C之间所产生的相对空间偏移会进一步增大两磁铁间距,因此磁铁A和C之间的作用磁力FAC或FCA可忽略不考虑。于是悬臂梁a受到的磁力作用,可只考虑其自由端磁铁A受到磁铁B的作用磁力FBA,即:
(5)
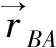
(6)
(7)
(8)
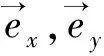
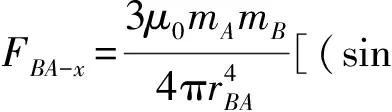
sinφ1cos (β1+β3)-5sinβ1cosα1cos(β1+β3)]
(9)

cosφ1cos(β1+β3)-5cosα1cosβ1cos(β1+β3)]
(10)

图4 磁偶极子求磁铁力的空间作用示意图Fig.4 Geometries of the three equivalent magnetic dipoles
同理对于悬臂梁c,它只受到磁铁B的作用。当磁铁B对磁铁C作用时,假设磁铁B只沿y轴振动,磁铁C只沿z轴振动,忽略磁铁B和C在x方向上的位移变化,那么B和C磁偶极子的距离rBC在yoz平面内,磁矩mB仍在xoy平面内,磁铁C的磁矩mC与y轴平行,如图4所示。于是磁铁C受到磁铁B的磁力计算式为:
(11)


(12)

(13)
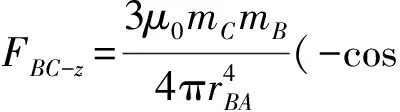
(14)
悬臂梁b受到的磁力是磁铁A和C对其自由端磁铁B的磁作用力的合力。有了各悬臂梁的磁力分析后,即可给出各悬臂梁的势能函数。
2.2 势函数分析
悬臂梁a所具有的势能包括弹性势能、重力势能和磁铁力FBA-x在x方向上所做的功。这里需要说明的是,在梁a振动的偏转角度范围内,其末端磁铁A沿y轴向的位移很小,且可以得到FBA-y沿y轴和FAB-x沿x轴所做功的关系WFBA-y<0.01WBA-x,因此FBA-y对梁a所做的功可忽略不计。同理,FAB-x对梁b所做的功以及FBC-x对梁c所做的功均可忽略。于是悬臂梁a在t0时刻位置x(t0)=x0的势函数为:
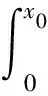
(15)
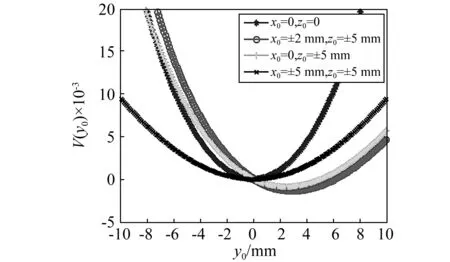
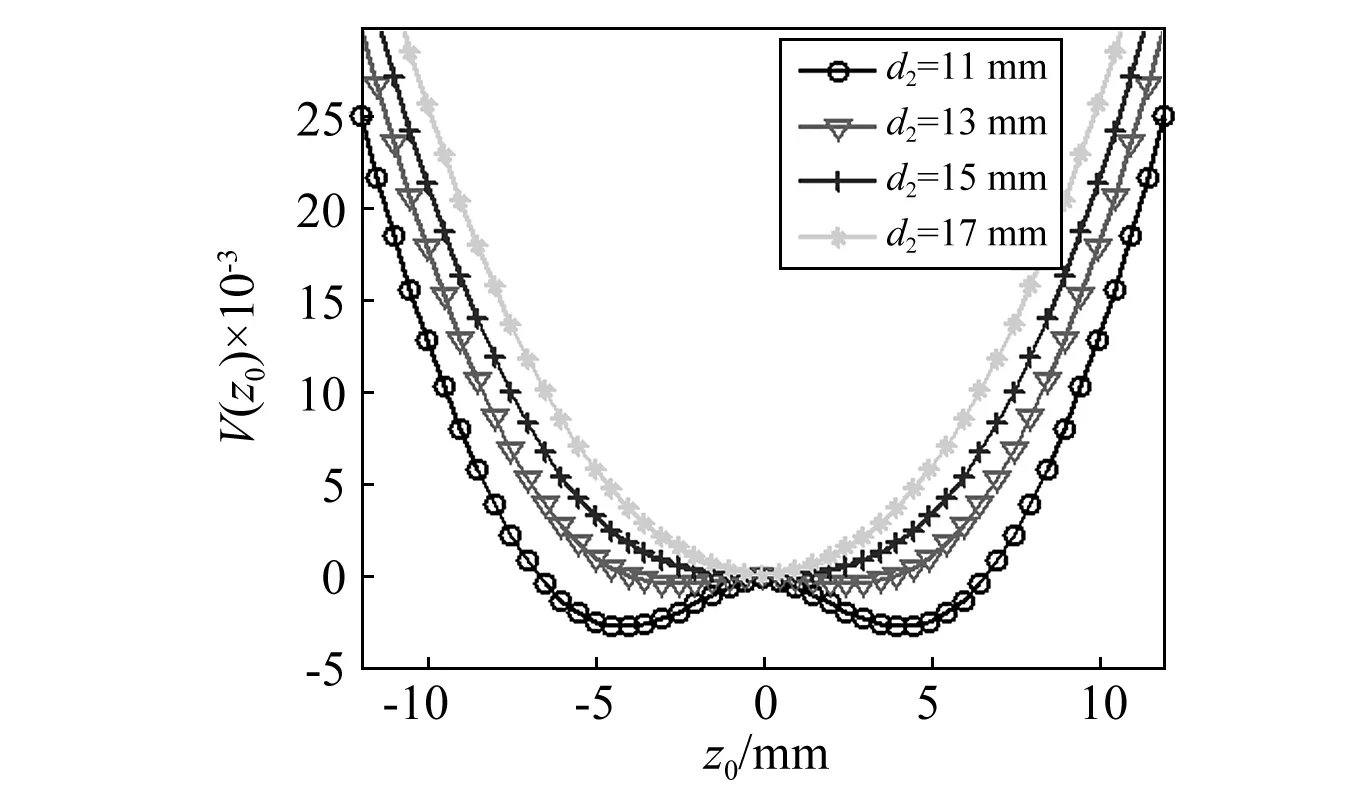
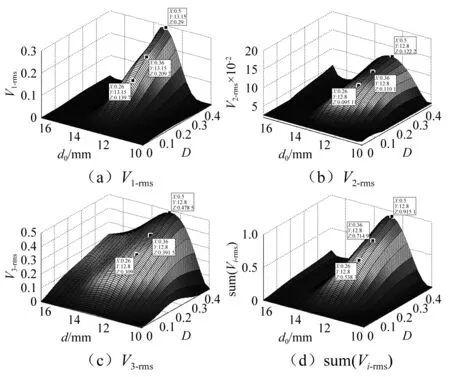
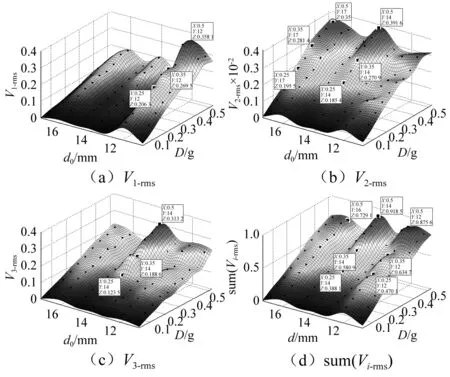
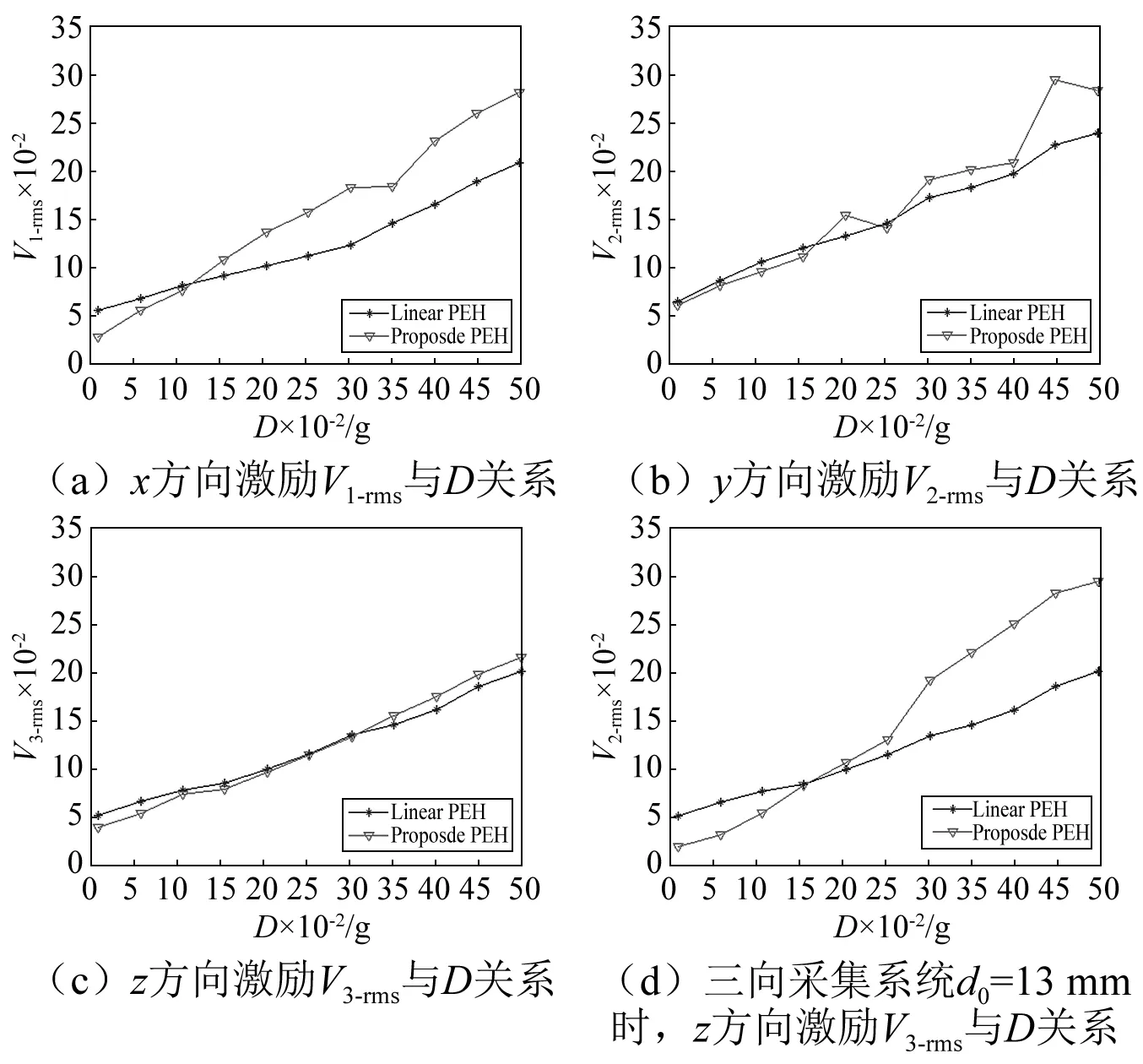
在系统振动过程中,由于磁铁A和B的间距d1(0 图5 不同磁铁间距d1对应梁a的势函数Fig.5 Effect of d1 and d2 on potential function of cantilever a 由图5可知,当磁铁间距很大时,如d1=17 mm,梁a的势函数近乎成单稳态,只在原点处出现一个稳定平衡位置,梁a的振动状态接近线性特征。而随着d1的减小,梁a的势函数也由单稳态逐渐转变成为双稳态,具有两个对称势阱的稳定平衡位置和一个不稳定的原点平衡位置,梁a的振动状态逐渐转变成非线性状态。梁a振动过程使其势函数不断发生变化的特性有利于促进机电能量的转换,因为当梁a处于某个较深势阱进行单阱振荡时,梁b的振动总会在某一时刻使磁铁间距d1增大,磁铁间距的增大使得梁a势阱变浅,势阱变浅必然为梁a越过势垒产生跃迁创造机会,跃迁机率的增大带来跃迁频率的提升,进而促进压电梁a产生频繁双稳跃迁振荡,达到提升机电能量转换的目的。 悬臂梁b的势能包括弹性势能、磁铁力FAB-y和FCB-y在y方向上所做的功,假设磁铁B只沿y方向运动,不考虑其重力在x方向的做功,则在t0时刻位置y(t0)=y0的梁b的势函数为: (16) 表2 三向采集系统的几何参数 在表1和表2参数以及初始磁铁间距分别为12 mm和14 mm条件下,图6给出了梁b不同振动时刻t0对应梁a和梁c分别不同位置x(t0)=x0和z(t0)=z0的势函数,这里讨论梁a和梁c的不同位置而不讨论磁铁不同位置的间距,是因为梁a和梁c分别在xoy和xoz两不同平面内振动,梁a和梁c位置的变化要比其投影到y轴的磁铁间距d1或d2的变化更能清晰理解梁b势函数的成因机制。以图6(a)为例,当某一时刻梁a和梁c同时处于平衡位置(x0=z0=0)时,梁b的势函数为非线性单稳态,此时由于磁铁A和C的间距最短,因此势函数曲线较陡。当梁c偏离平衡位置而梁a仍然处于平衡位置(如x0=0,z0=±5 mm)时,虽然磁铁A和C的间距有所增大,但梁b的势函数依旧保持单稳态,只是其稳定点向右发生了偏移。同理,当梁c处于平衡位置而梁a偏离平衡位置(如x0=±5 mm,z0=0)时,根据对称性梁b的势函数仍然保持单稳态,且其稳定点向左发生了偏移。对于梁a和梁c都偏离平衡位置时,如果两个梁的偏离量一致(如x0=z0=±5 mm)时,那么梁b的势函数是一个较为平缓的稳定点在原点的单稳态,如果两个梁的偏离量不一致(如x0=±2 mm,z0=±5 mm),那么梁b的势函数是一个稳定点偏离原点的单稳态。虽然悬臂梁b的势函数始终保持单稳特性,没有跃迁的双稳特性,但是由于其势函数在系统振动过程中稳定点不断发生移动改变,而且势阱形状也不断改变,因此相比于稳定点固定形状不变的单稳振荡,悬臂梁b的振荡幅度变化要大,其机电能量转换效果要好。 (a) d0 =12 mm (b) d0 =14 mm图6 梁a和梁c不同振动位置对应梁b的势函数Fig.6 Effect of d1 and d2 on potential function of cantilever b 图6(b)与图6(a)势函数的区别是不同初始磁铁间距引起势函数曲线的弯曲程度不同,当d0较大时,如图6(b),由于磁力减小,因此势函数弯曲程度减小,即势函数相对变平缓且势阱变潜。 悬臂梁c的势函数可根据梁a和b的分析方法得到,在此不再赘述。梁c在t0时刻位置z(t0)=z0的势函数为: (17) 图7是不同振动时刻在磁铁B和C间距d2(0 图7 不同磁铁间距d2对应梁c的势函数Fig. 7 Effect of d1 and d2 on potential function of cantilever c 为了模拟环境中的低频振动特征,振动激励取为0~120 Hz带宽的高斯随机激励。根据文献[16-18],在表1和表2材料属性参数与几何尺寸参数条件下,研究不同激励强度和不同初始磁铁间距下三向采集系统的输出电压规律。模拟中为避免系统振动过程可能出现磁铁B与磁铁A或C干涉接触而降低能量采集效果,将激励强度设定在0.05~0.5范围内,且初始磁铁间距取为d0>10 mm。各压电梁的输出电压以有效值Vi-rms进行衡量。 对式(1)~(4)采用四阶龙格库塔法进行数值计算,分别得到三向采集系统各梁电压响应的有效值Vi-rms与激励强度D和初始磁铁间距d0的关系,如图8所示,其中图8(a)、(b)、(c)分别表示梁a、梁b、梁c输出电压的有效值V1-rms、V2-rms、V3-rms随D和d0的变化关系,图8(d)是三个压电悬臂梁输出电压有效值之和sum(Vi-rms)(即系统的总体输出电压)随D和d0的变化关系。 图8可知,每个梁都存在一个最优初始磁铁间距使梁的输出电压达到峰值,大于或小于这一间距,梁的输出电压均会下降。梁a、梁b、梁c的最优间距分别为11.75 mm、11.4 mm、11.75 mm,虽然不存在一个共同的间距能够同时满足三个梁达到最大输出电压,但是从系统总体输出电压图8(d)可知,在x方向激励时,系统总输出最大电压存在唯一一个最优初始磁铁间距dopt=11.75 mm,确定这一“唯一”的最优间距,有利于能量采集系统适应实际变化的工况激励而无需实时调整结构参数进行工作,从而达到最有效的机电能量转换效果。 图8 x方向激励Vi-rms随D和d0的变化关系Fig.8 Dependence of Vi-rms on d0 and D in x direction excitation 按照x方向激励的分析方法,同理可得到z方向激励三向采集系统的输出电压Vi-rms与D和d0的关系,如图9。可以看出,与x方向激励相似,三个梁的最优磁铁间距仍然存在差别,但系统总输出的最优初始磁铁间距却是一个值12.8 mm。因此,对于实际z方向激励情况,系统可在一个最优间距下进行无结构参数实时调整的最有效能量采集工作。 同样,图10是y方向激励三向采集系统的输出电压Vi-rms与D和d0的关系,从图10(a)、(b)、(c)看出,梁a、梁b、梁c的最优间距分别为11.05 mm、11.75 mm、11.4 mm,三个梁的最大输出电压的最优间距不一致,但图10(d)系统总输出最大电压的最优初始磁铁间距dopt=11.75 mm却是唯一的,因此系统可在一个最优间距下,无需实时调整结构参数而适应y方向实际变化的工况激励进行有效能量采集。需要注意的是,当磁铁间距增大时,梁b的电压输出存在着一个上升趋势,这是因为两对磁铁间的斥力随间距增大逐渐减小,对梁b的振动限制减弱,于是梁b的振动幅度逐渐增大。 图9 z方向激励Vi-rms随D和d0的变化关系Fig.9 Dependence of Vi-rms on d0 and D in z direction excitation 图10 y方向激励Vi-rms随D和d0的变化关系Fig.10 Dependence of Vi-rms on d0 and D in y direction excitation 上述x,y,z三个方向的一定带宽和一定强度激励的模拟分析表明,从总体采集输出电压看,为了得到最大电能输出,三向能量采集系统在x和y两个方向的激励能够取得一致的最优初始磁铁间距。而在z方向的激励其最优初始磁铁间距要略大于其它两方向的。 为方便分析,令激励力方向与x,y,z轴均分别呈45°角,得到图11该方向激励下系统的输出电压Vi-rms与D和d0的关系。从图中可以看出,梁a、梁b、梁c的最优间距分别为11.4 mm、10 mm、11.4 mm,三个梁的最大输出电压的最优间距仍然不一致,但图11(d)系统总输出最大电压的最优初始磁铁间距dopt=11.05 mm却是唯一的,因此系统仍然可在一个最优间距下,能够有效的将激励能量转换成电能。 图11 空间任意激励Vi-rms随D和d0的变化关系Fig.10 Dependence of Vi-rms on d0 and D in Spatial excitation 为了验证前面的理论分析与仿真结果,根据表1和表2的参数数据制作了三向压电悬臂梁振动能量采集系统。压电陶瓷的型号为PZT-5A,采用双晶片结构,两层压电陶瓷片同极化方向排列,与中间电极层紧密粘接[19-20]。在压电陶瓷的上下表面焊接有导线,作为电压输出端。悬臂梁基体的材料为矽钢,永磁铁A, B和C为铁氧体磁铁,牌号为N35。三个悬臂梁固定在直角基座上,基座与激振台固定连接,如图12所示。 (a)主视图 (b)俯视图图12 三向振动能量采集系统实验结构图Fig.12 Experimental structures of three-dimensional energy harvester prototype 整个实验测试系统框架如图13所示,主要由信号发生器、功率放大器、激振器、三向振动能量采集器、数据采集器和微型计算机组成,信号发生器的型号为Agilent 33500B,功放的型号为MC LA-500,激振器的型号为MC VT-300,数据采集器的型号为NI 9234采集模块。实验中,信号发生器产生0~120 Hz带宽的不同强度的随机激励,该激励经过功率放大器并通过激振器产生振动作用于三向采集系统上,系统振动使其悬臂梁上的压电片产生电压,该电压由数据采集器进行采集,并由计算机进行分析。实验中为实现仅在单一方向上激励三向能量采集系统,将激振器振动方向始终与重力方向垂直(或与地面平行)放置,并通过垂直换向装置将三向能量采集系统换向。为避免磁铁间距太近而导致磁铁发生碰撞,或者太远的磁铁间距使磁力影响过小,实验选取初始磁铁间距在[11 mm,18 mm]范围内进行调节。实验激励强度D以振动的加速度有效值来表示,其强度范围选取在[0.05 g, 0.5 g]区间。负载电阻为8 kΩ,实验结果以输出电压的均方根值Vi-rms来表示,系统的输出功率P可以通过P=Vi-rms2/RL的计算得到。 图13 三向振动能量采集系统实验测试框图Fig.13 Experimental test system of the three-dimensional energy harvester prototype 仿照图8绘制出系统实验输出电压Vi-rms与激励强度D和初始磁铁间距d0的三维关系图,如图14所示。其中黑色点表示实验输出电压有效值结果,三维曲线通过差值算法进行拟合。可以看出,系统中三个梁的输出特性与仿真结果的趋势基本一致,且均存在一个最大输出电压对应的最优间距,更重要的是三个梁的实验最优间距几乎一致,都在dopt=12 mm处,因此系统总输出的最优初始磁铁间距确定在d0=12 mm处。 图14 x方向激励实验Vi-rms以及随D和d0的变化关系Fig.14 Dependence of on d0 and D in x direction excitation experimental results 图15是Z方向激励下系统实验输出电压Vi-rms与激励强度D和初始磁铁间距d0的三维关系图,与x方向激励实验结果类似,系统中三个梁的输出特性与仿真结果的趋势基本一致,也都在相同的最优间距dopt=13 mm处取得最大输出电压,系统总输出的最优初始磁铁间距当然也是13 mm。 图15 z方向激励实验Vi-rms以及随D和d0的变化关系Fig.15 Dependence of Vi-rmson d0 and D in z direction excitation experimental results 图16为y方向激励下三向采集系统的输出电压Vi-rms与D和d0的关系。从图16 (a)、(b)、(c)三个图可以看到,梁a和梁c分别在12 mm和14 mm间距处取得最大输出电压,梁b在14 mm和17 mm两个间距处取得较为明显的峰值电压。这一实验结果与仿真结果有所偏差,就其原因在于,当d0=12 mm时,由于磁铁间距很近,磁铁间作用力较强,因此系统振动过程中发生了梁b自由端向梁c方向倾斜,导致磁铁A和B作用力减小到正好使梁a形成双稳跃迁振荡,而梁c由于磁铁C和B的作用力增强而形成单稳震荡,于是在12 mm间距处梁a达到峰值电压而梁c不能达到峰值电压。此时梁b因受两端较大磁力的限制,因此其单稳振荡幅度较小,发电量也较低。当磁铁初始间距增大至d0=14 mm时,磁铁A 、B、C间的作用力减小,系统振动使梁b自由端向梁c的倾斜减少,导致磁铁A、B作用力的减小不足以形成梁a的双稳跃迁振荡,而此时磁铁C、B作用力的减小正好形成梁c的双稳跃迁振荡。因此在14 mm间距处梁a不能输出峰值电压而梁c可输出峰值电压。对于梁b而言,因其两端磁力减小且势阱变缓而使其单稳振荡幅度增大,因此其发电量提高并达到大峰值电压输出。当磁铁初始间距进一步增大至d0=17 mm时,磁铁A、B、C间的作用力进一步减小,导致系统的振动均不能使梁a和梁c形成双稳跃迁振荡,因此梁a和梁c发电效果较差。而梁b自由端因其两端磁力进一步减小,可以认为梁b几乎是无倾斜的单稳大幅度振荡,但因为没有梁a或梁c双稳振荡的促进作用,其振荡幅度要低于14 mm间距的振荡幅度,因此梁b的17 mm间距比14 mm间距的峰值电压略小。 从图16(d)系统总输出情况看,存在三个较优的初始磁铁间距12 mm、14 mm和16 mm可使系统输出峰值电压相当。考虑到x和z方向激励系统总输出峰值电压的最优初始磁铁间距12 mm和13 mm,相比较而言,应用中可选取d0=12 mm作为系统的最优初始磁铁间距。 图16 y方向激励实验Vi-rms以及随D和d0的变化关系Fig.16 Dependence of Vi-rmson d0and D in y direction excitation experimental results 将图1中3个永磁铁A、B和C分别替换为相同质量和相同尺寸的非磁性质量块,其它部件结构、尺寸位置及字母编号不变,则构成传统的三向线性压电悬臂梁振动能量采集系统(简称三向线性采集系统)。以此传统的三向线性采集系统为参照,对比分析本文提出的三向采集系统的振动能量采集效果。 当实验测量的振动分别在x,y,z三个方向激励时,传统的三向线性采集系统和本文提出的三向采集系统中,各自的悬臂梁a, b, c的电压响应V1-rms、V2-rms、V3-rms分别与激励强度D的关系如图17(a)、(b)、(c)所示,其中本文提出的三向采集系统的磁铁间距均选择调整在最优初始磁铁间距d0=12 mm状态。从图(a)x方向激励的V1-rms-D关系可知,本文提出的三向采集系统梁a的电压输出V1-rms在D>0.13时高于常规三向线性采集系统梁a的电压输出,而D<0.13时不如线性能量采集系统;图17(b)y方向激励的V2-rms-D关系可知,在激励强度相对较大时,本文提出的三维能量采集系统梁b的电压输出略高于线性梁;对于图(c)z方向激励的V3-rms-D关系,由于d0=12 mm不是此方向激励下三向采集系统的最优初始磁铁间距,因而本文三向采集系统梁c的电压响应曲线与常规三向线性采集系统的较为接近,两系统输出电压值近似。如果取z方向激励的最优磁铁间距d0=13 mm,当激励强度足够使其产生双稳大幅度的跃迁响应时,三向采集系统相比于三向线性采集系统,其梁c的输出电压普遍要高得多,如图17(d)所示。 图17 常规的三向线性采集系统与本文提出的三向采集系统(d0=12 mm)的Vi-rms与D的关系Fig.17 Dependence of Vi-rms and D of traditional linear piezoelectric energy harvester system and proposed PEH 图18 (a)、(b)、(c)是常规的三向线性采集系统和本文提出的三向采集系统分别在x,y,z方向激励下,各系统三个梁的总体输出电压的均方根值之和sum(Vi-rms)与激励强度D的关系,其中三向采集系统的初始磁铁间距选择在d0=12 mm处。可以看到,无论在哪个激励方向上,当环境激励的强度相对较大时,三向采集系统比三向线性采集系统的能量获取都有着明显的优势,这得益于三向采集系统所具有的非线性双稳和单稳运动特性,不论x,y,z中哪个方向的振动激励,都能使三个梁产生运动同时实现机电能量转换。而当激励强度较小时,由于梁a和梁c不容易产生双稳跃迁,因此在单一势阱中震荡,导致输出低于线性能量采集结构。此外,对于图18(c)z方向激励,三向采集系统的总体输出电压低于其它两方向激励系统的总体输出电压,其原因也是因为d0=12 mm不是z方向激励下三向采集系统的最优初始磁铁间距,如果取z方向激励的最优磁铁间距d0=13 mm,那么同样可以看到三向采集系统在z方向的总体输出电压大大提高,如图18(d)所示。 图18 常规的三向线性采集系统与本文提出的三向采集系统(d0=12 mm)的总体输出电压sum(Vi-rms)与激励强度D的关系Fig.18 Dependence of sum(Vi-rms) and D of traditional linear piezoelectric energy harvester system and proposed PEH 实际环境中的振动可以来自三维空间中的任意方向,为了能够采集实际环境中各个方向的振动能量,本文提出了一种三向压电悬臂梁式振动能量采集系统,这种能量采集系统仅利用3个压电悬臂梁的非线性结构方式,即可同时俘获空间各个方向的振动能量。数值模拟和实验分析结果表明,对于材料和尺寸结构均相同的3个压电梁所构成的非线性能量采集系统,以及对于一定带宽和一定强度范围的随机激励,在空间三个相互垂直的方向上,系统的总体输出电压均可在一个最优的初始磁铁间距处获得最大峰值,系统在三个方向的最优初始磁铁间距中,有一个方向的最优间距略偏离开另外两个方向相同的最优间距。为满足实际振动环境无结构参数调整的实时能量采集,解决的方法是将初始磁铁间距按照两个方向一致的最优间距取值确定,以保证最多的能量采集。




3 数值计算与仿真分析
3.1 x方向激励

3.2 z方向激励
3.3 y方向激励
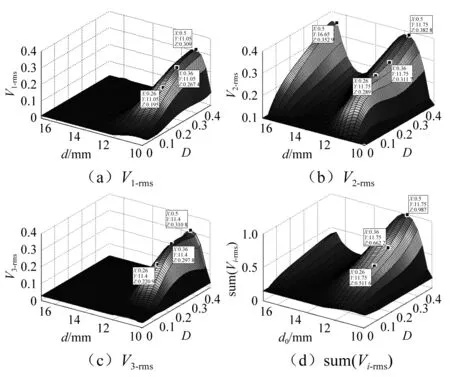
3.4 空间任意方向激励
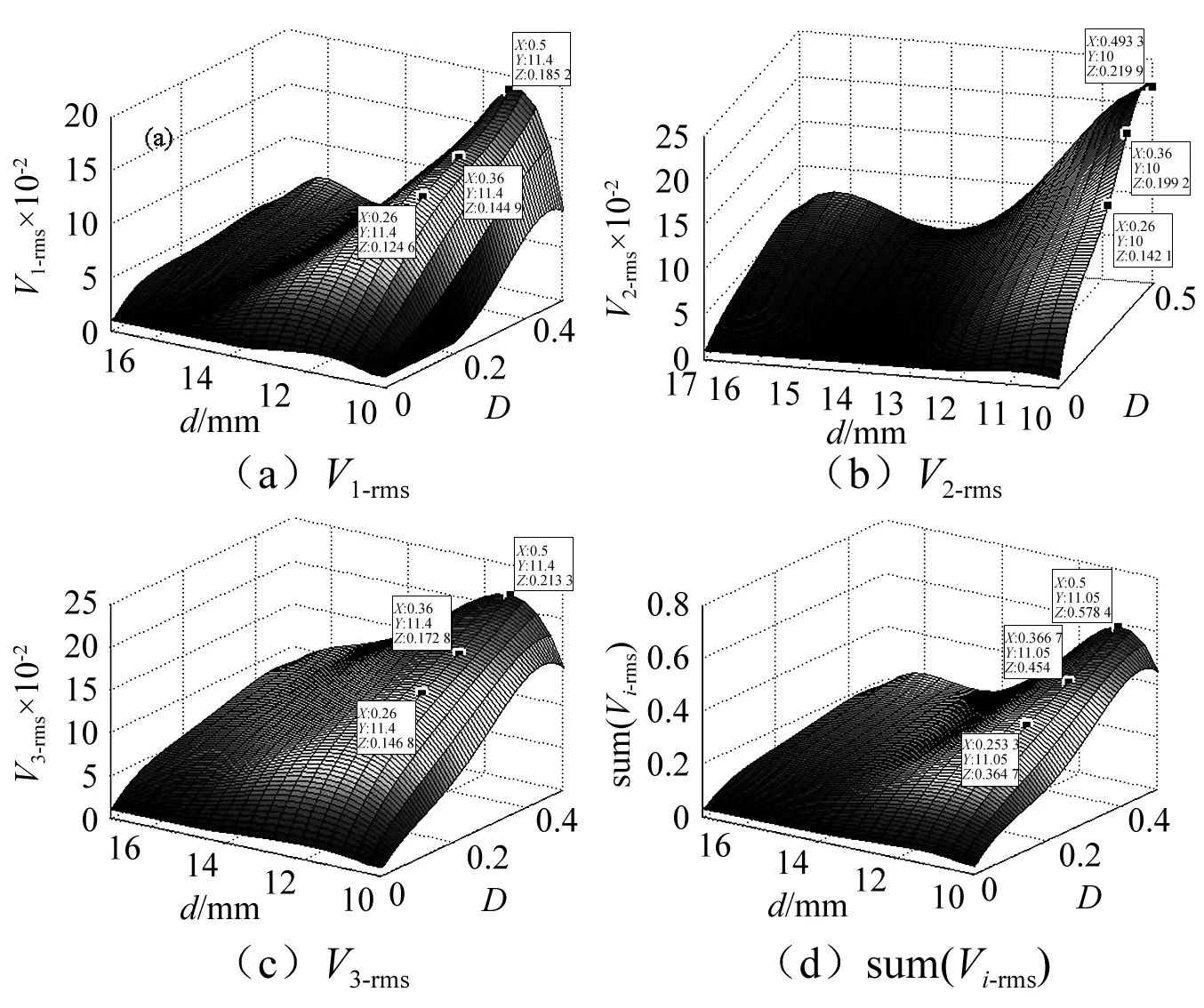
4 实验分析



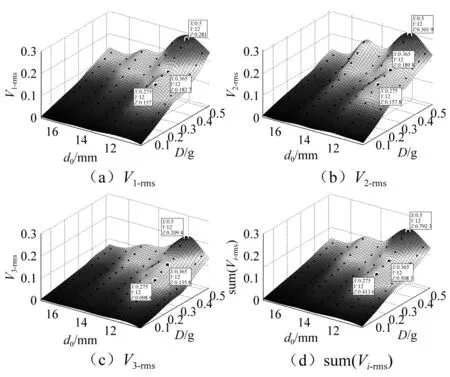
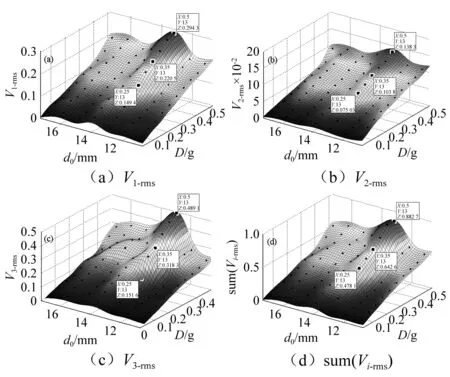
5 与线性能量采集结构效果的对比分析

6 结 论

