关于稀疏编码在图像处理中的神经动力学分析
卢颍霞, 王如彬
(上海华东理工大学 认知神经动力研究所, 上海 200237)
稀疏性是一个令人感兴趣的内容,部分是因为它为后期的处理提供一个简单的编码。早期虽然有皮层稀疏编码(对于作用于同一刺激的神经元集群来说,并不是所有的神经元都被激活,只有少数神经元被激活)的实验结果[1-6],但同时也有许多神经元同时发放的实验[8]。
所以没有一个绝对的标准去评价皮层神经元的相对稀疏性。神经生理研究已表明:初级视皮层中单个神经元仅对处于其感受野中的刺激作出反应,其空间感受野被描述为具有局部性、方向性和带通特性的信号编码滤波器。而每个神经元对这些刺激的表达则采用了稀疏编码原则,将图像在边缘,端点,条纹等方面的特性以稀疏编码的形式进行描述。
自然图像的稀疏编码算法能够准确预测视皮层神经元的特点,从而我们可以通过计算自然图像的稀疏表达来研究V1区简单细胞的感受野。Olshausen等[9-10]建立了一些自然图像的稀疏编码模型,但缺点是缺乏局部突触可塑性的生理学依据,无法全面的说明初级视皮层V1区神经细胞采用稀疏编码的形式来有效表示自然场景。
生物神经网络中存在一种竞争现象,即一个神经细胞兴奋后,通过它的分支会抑制周围其它细胞的发放,这种抑制作用使细胞之间出现竞争。模型表明由于竞争学习,齿状回的发放活动是稀疏的,但是该模型没有研究竞争学习对V1区简单细胞发放活动的影响[11]。
STDP(Spike Trigger Dependent Plastic)是一个简单有效的学习规则[13-14],并且在我们大脑神经元的连接方式的改变中扮演着重要的角色[12]。STDP是一个突触学习规则,只与突触前神经和突触后神经有关,突触前神经元和突触后神经元之间的动作电位的相对时间决定了突触可塑性的强度。最近Clopath等[15]利用了STDP的一种形式,但是没有发现和V1区类似的Gabor类感受野。Rehn等[16]建立的SSC(Sparse-Set Coding)模型,虽然通过STDP和发放神经元来研究V1区简单细胞的感受野,但没有进一步讨论网络中细胞数量对网络稀疏表达的影响,而在大多数神经网络中,兴奋细胞和抑制细胞的数量比约为4∶1[19]。
为了改进以上模型,我们利用STDP的一种学习规则,基于局部竞争的生理学现象建立了一个整合发放LIF(Leaky Intergate-and-Fire)的神经网络动力学模型。通过我们的模型得到了和猕猴V1区简单细胞类似的Gabor类感受野,并且利用细胞脉冲光栅图给出了细胞在不同时间步的稀疏发放活动。由于在大多数神经网络中,兴奋性细胞和抑制性细胞的数量比约为4∶1,从而我们考虑了不同数量的兴奋性细胞和抑制性细胞对网络稀疏表达的影响,发现由于细胞间的竞争学习,随着细胞数量的增加,细胞的抑制连接权重增加。模型中细胞的脉冲输出构成了图像的稀疏表示,并且利用它们的线性组合可以实现图像重构,通过对重构残差的讨论,发现在细胞数量比为4∶1的情况下,可以利用较少的细胞实现图像重构。
1 稀疏编码模型
首先介绍一下简化的整合发放神经元的电路图(见图1),其中Iinput代表输入电流,电容器模拟膜电压,当电压超过阈值θi时,二极管打开,发放一个脉冲或动作电位,R模拟膜电阻,Vout模拟输出。
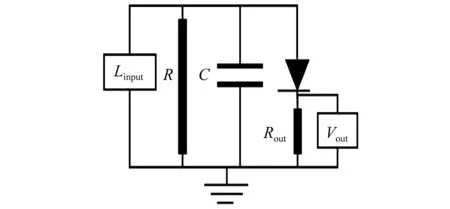
图1 简化的整合发放神经元的电路图Fig.1 Diagram of simplified integration of neurons
我们的模型由156个兴奋性细胞和40个抑制性细胞两部分组成,其中细胞之间是全连接,所有的细胞接收自然场景的白化的10×10像素(每个图像块)的图像(Olshausen, Field, 1996)输入,这些细胞的脉冲输出构成图像的稀疏表示,见图2。
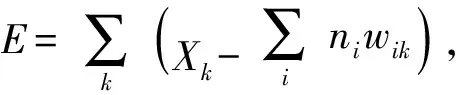
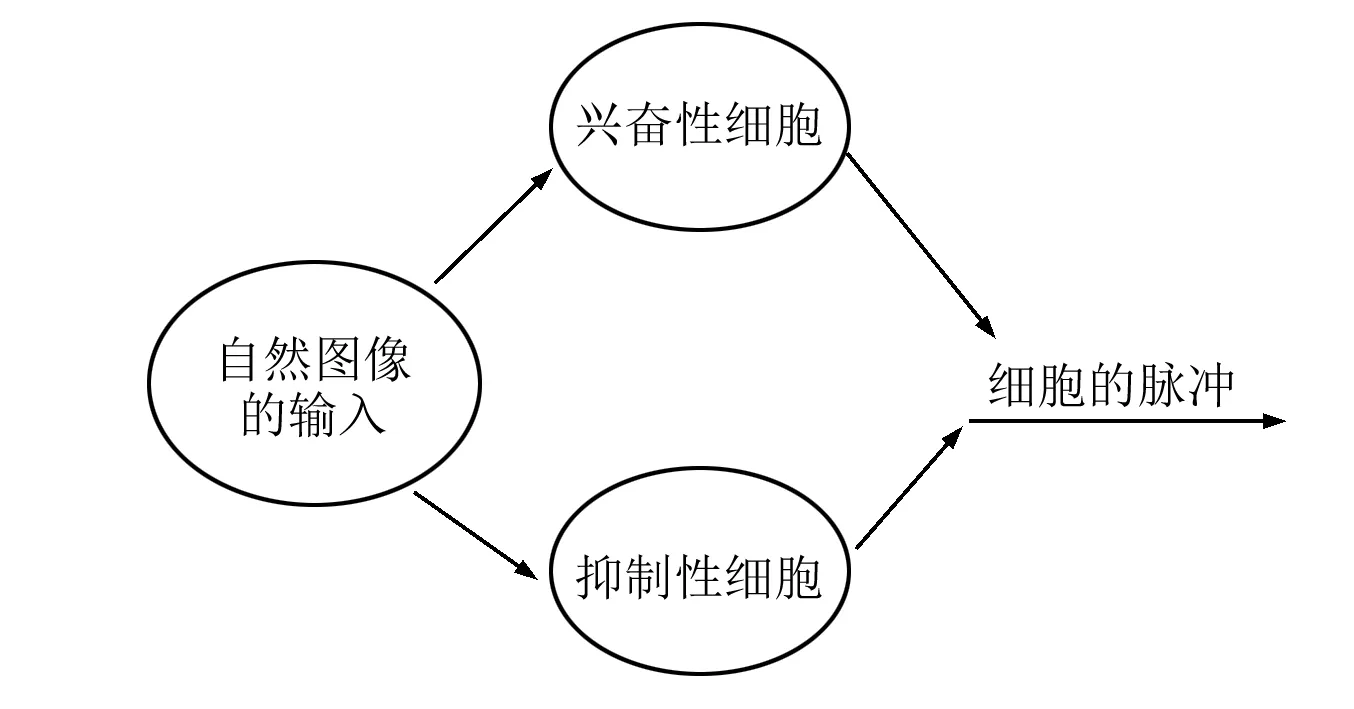
图2 新的整合发放神经元网络模型Fig.2 New integrated release of the neural network model
对于每个时间步t,每个神经元i的状态按下面的规则变化:
(1)
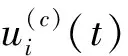
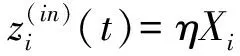
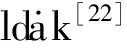
式中:p(c)表示c类神经元的目标平均发放率,对于每个时间单位p(E)=0.02,p(I)=0.04,τ(E)=1,τ(I)=0.5。
兴奋性细胞和抑制性细胞的权重变化依据赫布可塑性规则[23]。图像对于细胞的权重变化W(in→E/I)根据赫布规则“HO(Hebbian-Oja)”,兴奋性细胞对兴奋性细胞W(E→E)和兴奋性细胞对抑制性细胞W(E→I)的权重变化根据相关度准则“CM(Correlation Measuring)”,即:
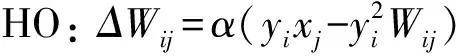
方程中xj代表突触前神经元j的发放率,yi代表突触后神经元i的发放率。
当10 000个训练样本的权重的RMS不再下降即ΔWij=0,网络达到平衡状态:
式中:nj和mk分别代表兴奋性细胞j和抑制性细胞k关于短时间窗Δt的输出脉冲。
2 结 果
利用我们的模型不仅可以得到V1区简单细胞的稀疏编码以及细胞数量对网络稀疏表达的影响,而且讨论了兴奋性细胞和抑制性细胞的数量对重构残差的影响。
在推理阶段,LIF神经元接收外界白化的图像刺激,这个时期网络的细胞脉冲输出构成图像的稀疏表示,该阶段的推理主要通过脉冲进行,当神经元发放一个脉冲时,在下个时间步,它抑制或兴奋突触后神经元。在学习阶段,神经元权重的更新主要是根据相关度准则(CM),只跟突触前神经元和突触后神经元的发放活动有关。
图3(a)是猕猴的感受野[24],图3(b)是我们得到的156个兴奋性细胞的感受野,每个方块代表一个神经元的感受野,其中灰色代表零,亮色代表正值,暗色代表负值,从图中可以看出,模型得到的简单细胞的感受野和猕猴初级视皮层简单细胞的感受野类似(见附录),具有空间局部性,方向性和频域的带通性。

图3 我们的模型得到的初级视皮层简单细胞的感受野和猕猴初级视皮层简单细胞的感受野Fig.3 Our model obtained by the primary visual cortex of simple cells of the receptive field and the rhesus monkey primary visual cortex of simple cells of the receptive field
当网络的所有细胞接收同一ZCA白化的自然图像的输入时,神经元的发放活动由图4给出,从图中我们可以看到并不是所有的细胞在任何时间都是发放的即细胞的发放是稀疏的。
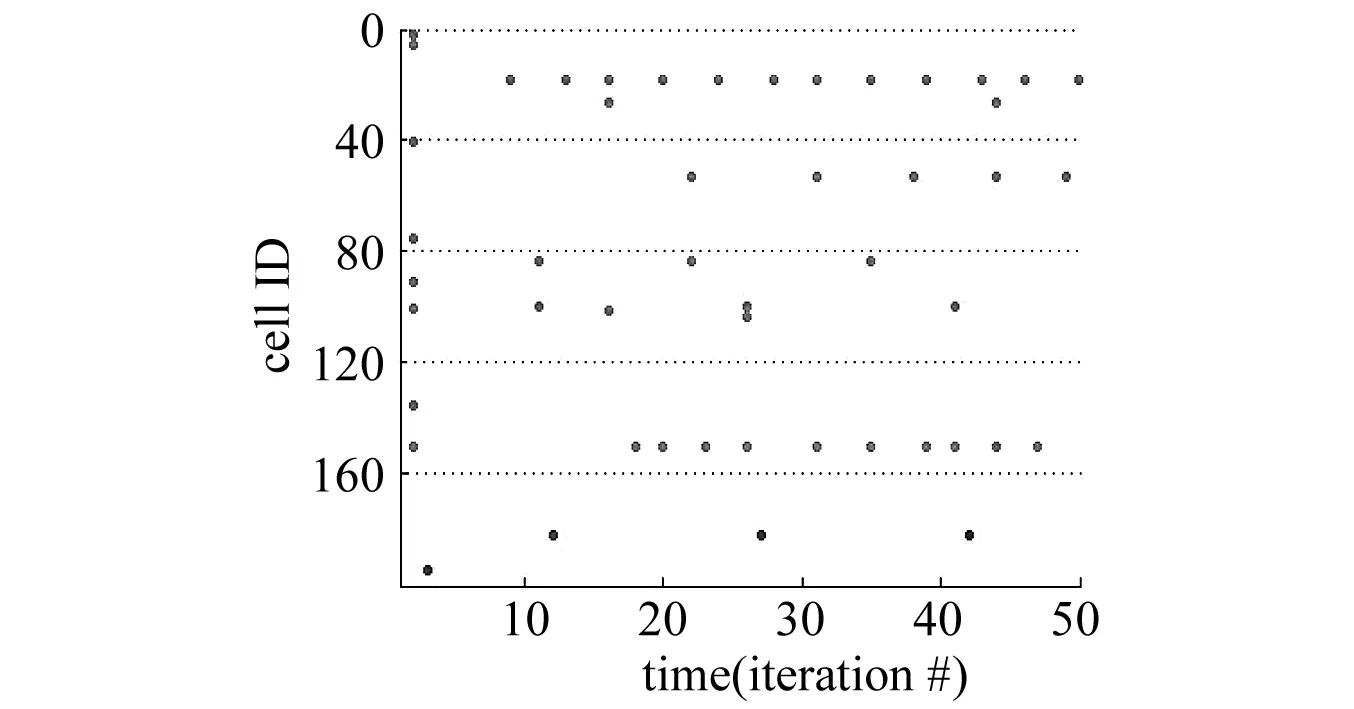
图4 细胞脉冲光栅图。图中的每一行都表示不同的细胞IDFig.4 Cell pulse grating. Each row in the figure represents a different cell ID, green indicates excitatory cells, and red indicates inhibition of cells
细胞的脉冲输出构成了图像的稀疏表示,并且利用它们的线性组合可以实现图像的重构,图5(a),从Olshausen和Field中选取的图像,图5(b),模型得到的以(a)作为输入的重构图像,可以看出我们得到的重构图像和原图像类似。

图5 模型得到的细胞的发放活动可以实现网络的图像重构Fig.5 Model of the cell release activities can be achieved on the network image reconstruction
由于在大多数神经网络中,兴奋性细胞和抑制性细胞的数量比约为4∶1,从而我们考虑了不同数量的兴奋性细胞和抑制性细胞对网络稀疏表达的影响。图6(a),对于10×10的图像块输入,改变兴奋性细胞和抑制性细胞的数量时,重构误差的变化。从图(b)中可以看出增加兴奋性细胞,重构误差是先减小后增大,并且继续增加细胞的数量时,误差没有出现减少的现象。图6(b),改变兴奋性细胞和抑制性细胞数量时,细胞抑制连接权重的变化,发现由于细胞间的竞争学习,随着细胞数量的增加,细胞的抑制连接权重增加,其结果具有一定的生理学依据,即细胞之间的竞争学习能够抑制V1区细胞的发放,进而增加了细胞的稀疏性质。
我们的模型主要是通过细胞之间的竞争学习形成稀疏编码。图6(a)给出了不同数量的兴奋性细胞和抑制性细胞对重构误差和细胞抑制连接权重的影响。当兴奋性细胞为156个,抑制细胞为40个时(此时兴奋性细胞和抑制性细胞的比例大约为4∶1),图像的重构误差达到最小。图6(c)是继续增加细胞的数量时,抑制性细胞开始出现冗余的现象(粗实线标出)。从图6(b),我们可以看出发现由于细胞间的竞争学习,随着细胞数量的增加,细胞的抑制连接权重增加。
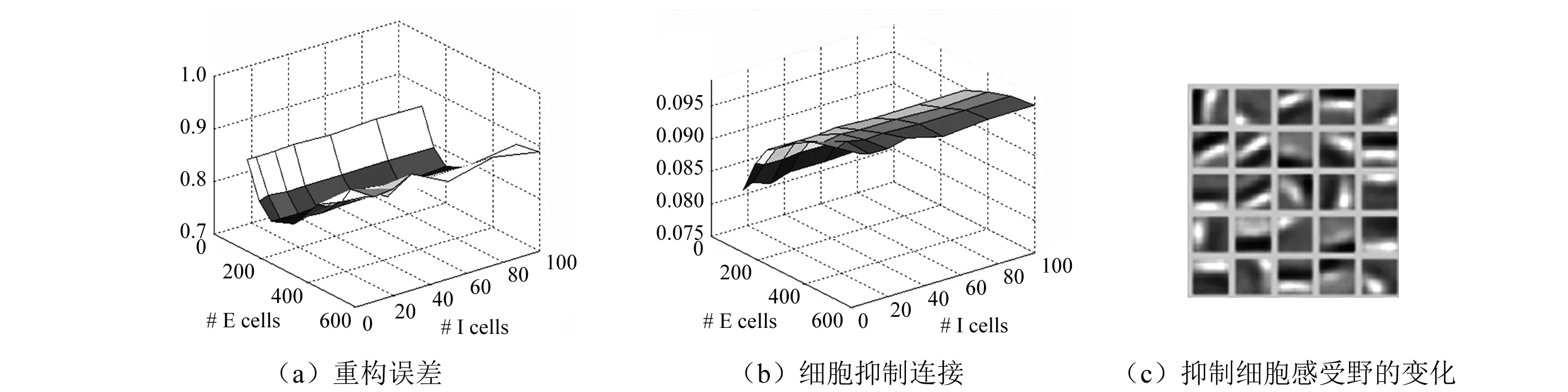
图6改变兴奋性细胞和抑制性细胞的数量时,重构误差,细胞抑制连接权重和抑制细胞感受野的变化Fig.6 When changing the number of excitatory and inhibitory cells, changes in the reconstructed errors, the cell-dependent link weights, the plots of the RF of the I cells
图7给出了模型的网络动力学行为,粗实线代表细胞的抑制反馈,细实线代表细胞的发放率,水平虚线代表平均值。网络接收图像输入(横坐标表示网络输入),当达到阈值时,细胞开始发放(细实线),此时细胞之间的抑制作用增加(粗实线)。从图中可以看出,只有达到一定阈值时,细胞才开始发放。其中对于细胞的图像输入形成高斯分布(虚线)。
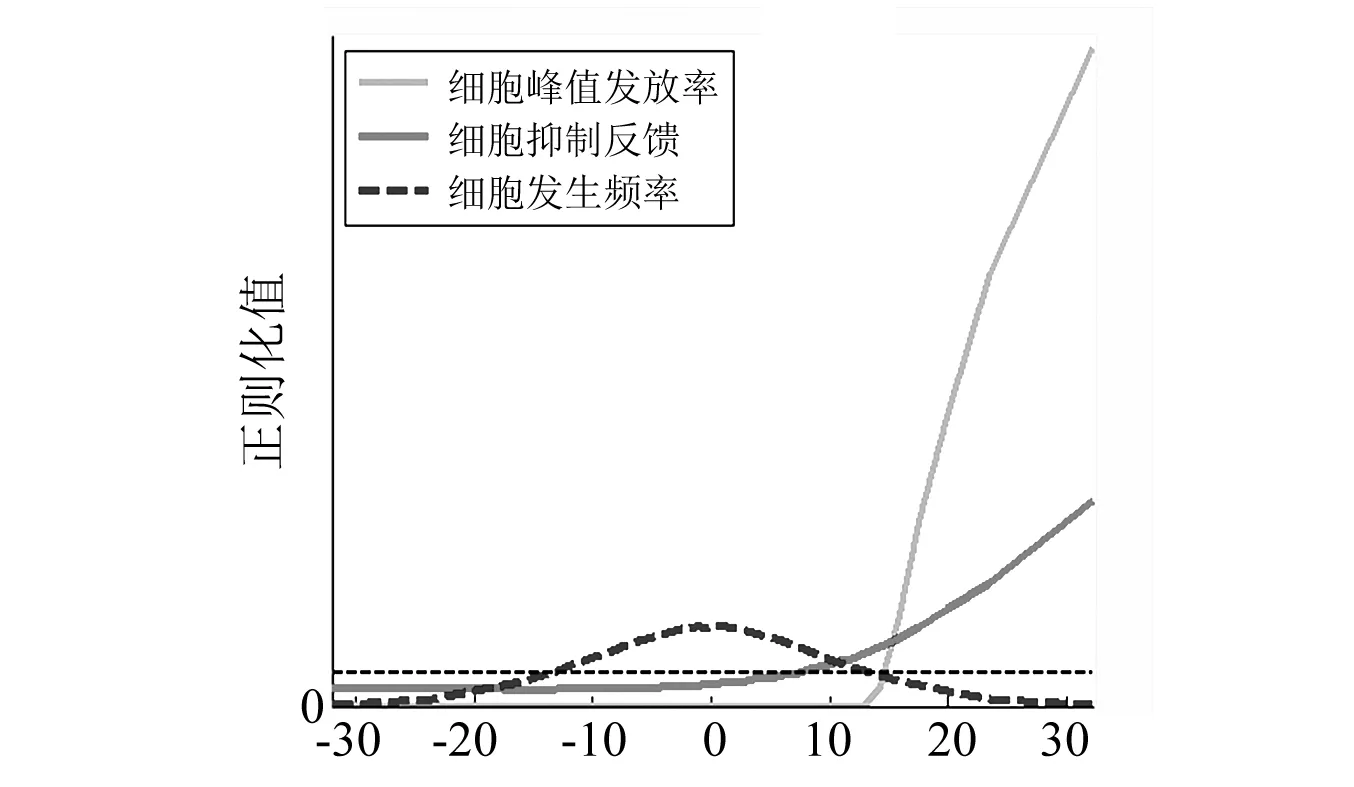
图7 网络动力学Fig.7 Network dynamics
3 讨 论
本文利用细胞之间的竞争学习,使网络的动力学行为表达在性质上具有稀疏性。
结论如下:
(1) 首先通过Matlab仿真得到了和猕猴初级视皮层简单细胞类似的Gabor类感受野,并且利用细胞脉冲光栅图给出了细胞在不同时间步的稀疏发放活动。
(2)其次讨论了不同数量的兴奋性细胞和抑制性细胞对网络稀疏表达的影响,发现由于细胞间的竞争学习,随着细胞数量的增加,细胞的抑制连接权重增加,即细胞之间的竞争学习能够抑制V1区细胞的发放,进而增加了细胞的稀疏性质[20]。
(3)最后通过稀疏重构系数,讨论了不同数量的兴奋性细胞和抑制性细胞对重构残差的影响,发现我们可以利用较少的细胞数量实现图像的重构。此时兴奋性细胞和抑制性细胞的比例接近4∶1。
我们模型中权重的变化不同于以前的模型[26-28],它依据突触可塑性准则,只与到达当前突触的脉冲数和突触后神经元生成的脉冲数有关。尽管模型比较简单,但是利用该模型可以发现V1区神经元的许多特点,例如细胞的竞争学习、神经元的稀疏发放、突触可塑性。我们希望这些发现可以帮助揭示视皮层的一些编码准则。

