具惯容离心摆的轴系结构轴向振动减振分析
秦美娟, 金肖玲, 陈志强, 黄志龙
(1.浙江大学 航空航天学院工程力学系,杭州 310027; 2.南京理工大学 自动化学院,南京 210094)
机械装置的振动很大程度影响着其使用寿命和工作效率,甚至引起破坏,如轴系结构的断轴事故。因此,结构的减振分析受到了很多研究者的关注,提出了各种振动抑制方法。离心摆减振器是被动减振器中的一种,早在1929年已发明应用于抑制内燃机的扭振[1],之后还广泛用于抑制轻型飞机发动机[2]、直升机旋翼[3]、船舶推进轴系[4]等的振动。一些轴系结构除了扭转振动还有其它形式的振动如轴向振动[5],在轴向振动的共振条件下轴向振幅显著增大[6],且现有资料表明:在轴系扭振得到较为完善的解决之后,断轴事故中60%~80%是轴向振动引起的[7]。1949年,Reed[8]利用离心摆减振器对轴系结构的轴向减振进行了理论分析并讨论了减振器的参数。Yoshida[9]通过振动平台和实际应用研究了离心摆减振器在船舶上层建筑减振方面的应用。Longoria 等[10]通过理论分析和设计离心摆减振器的摆参数及旋转速度来控制主结构的轴向振动,并通过实验验证。Hollkamp等[11]研究了质量集中的无阻尼速度跟踪离心摆减振器在发动机叶片振动中的应用。
近年来,“惯容”[12]作为一种新型的机械结构,得到了较多研究并在振动抑制领域取得了好的效果[13-15]。它是剑桥大学的Smith教授于2003年提出的,经过特别设计具有双端口,从而彻底实现了机械系统和电学系统的完全类比。Smith教授等分别针对平移运动和转动运动,设计了惯容的可实现机构形式[16]。将惯容器引入传统调谐质量阻尼器构成调谐质量惯容阻尼器,能显著提高系统的减振性能[17-18]。在随机激励的情形下,调谐质量惯容阻尼器比传统调谐质量阻尼器更有效[19]。
本文研究具惯容离心摆的轴系结构轴向振动的减振分析。将惯容引入离心摆减振器,分析主结构的轴向振动,讨论减振器参数对轴向振动的影响,并以主结构轴向振动的共振振幅最小为目标及结合离心摆做小幅扭转振动的限制条件,对离心摆减振器进行优化设计,得到最优的具惯容离心摆减振器参数。
1 系统动力学方程及其振动分析
图1为具惯容离心摆减振器的轴系结构示意图。主结构为轴系结构,中心轴以角速度ω1=nω旋转,转动式惯容安装在离心摆与主结构之间构成具惯容离心摆减振器。当轴系结构在轴向的外激励P0sin(ωt)作用下,x1方向(即轴向)振动是关注的核心。在轴上安装图示具惯容的离心摆减振器可抑制主结构的轴向振动,通过离心摆绕枢轴的微振θ来减小轴向振动x1。

图1 安装具惯容离心摆减振器的轴系结构示意图Fig.1 Schematic diagram of the shaft structure using centrifugal pendulum absorber with inerters
(1)
(2)
(3)
式中:m表示离心摆的质量;r表示离心摆质心到枢轴的水平距离;R表示枢轴到中心轴的水平距离;I1,I2,I3分别表示离心摆关于三个主轴的转动惯量。
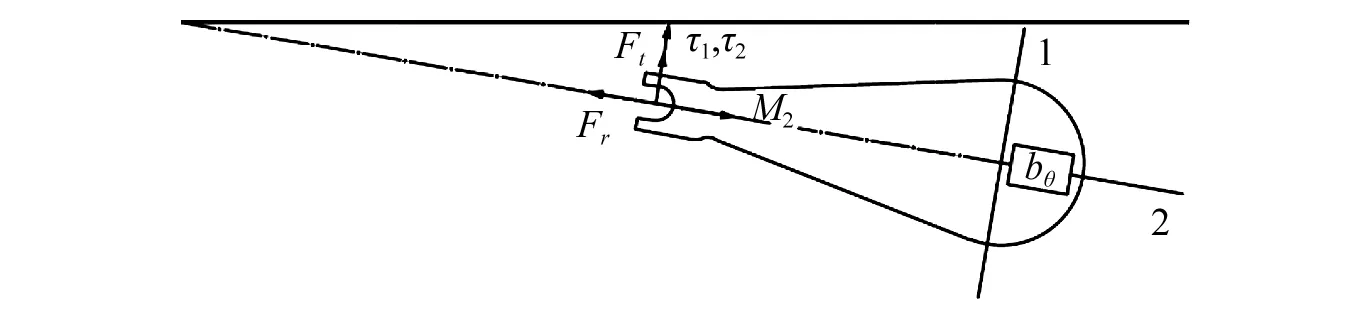
(a) 俯视图
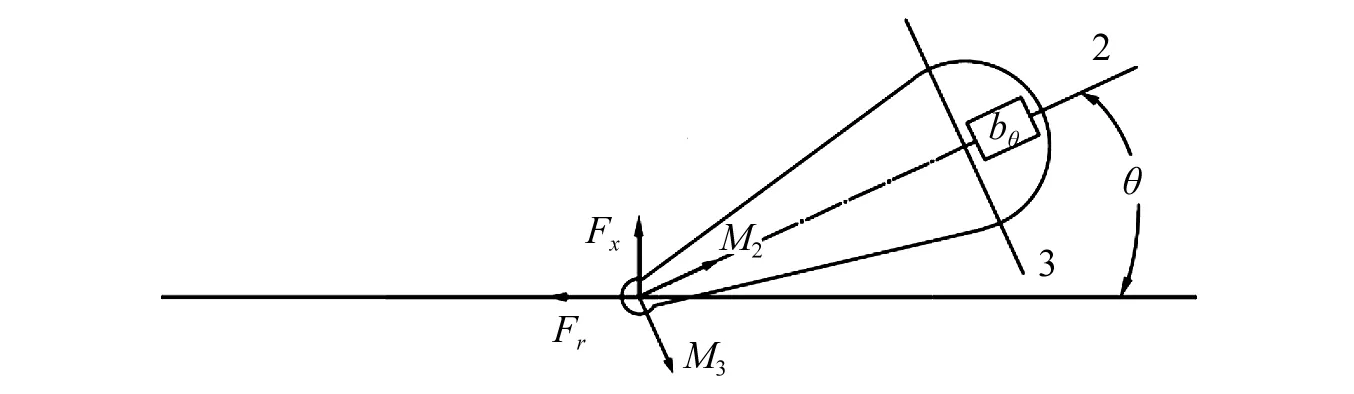
(b) 主视图
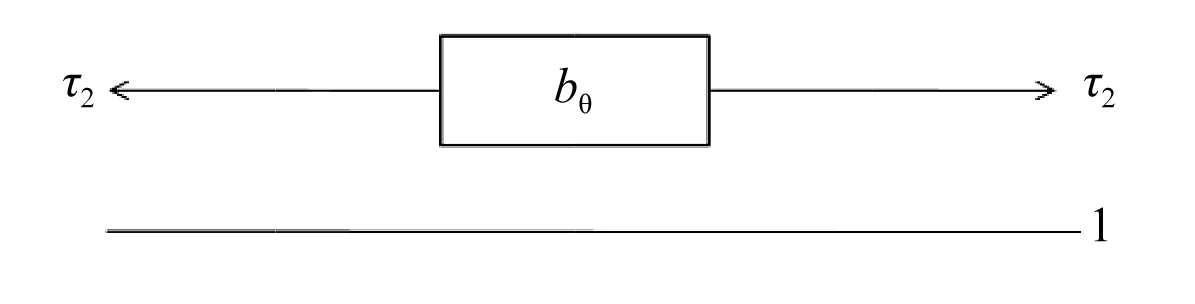
(c) 惯容俯视图图2 具惯容离心摆减振器的受力分析图Fig.2 Force diagram of the centrifugal pendulum absorber with inerters
利用集中参数法建立系统的动力学模型,图1主结构轴向振动可模型化为等效弹簧K和等效质量块M。本文研究主结构的轴向振动x1,主结构在轴向受到简谐力P0sin(ωt)外,还受到减振器的轴向力Fx。假设离心摆的振动是小幅振动,最终可得离心摆减振器和轴系耦合的动力学方程:
(4)
主结构的轴向振动可以表示为x1=x0sin(ωt+φ0),离心摆的转角θ=θ0sin(ωt+φ1)。为了便于分析,同时引入如下无量纲量:
(5)
(6)
(7)
(8)
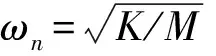
x0=xstH(T,C,β,S)
(9)
(10)
其中:
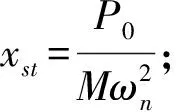
2 减振器参数对减振的影响及其优化设计
安装具惯容离心摆减振器的目的是降低主结构的线性振动,即减小x0。它由函数H确定。H随β的变化即为幅频响应曲线,是线性振动关注的重点,从H的表达式中可以看出H的值除了与β有关外,还与离心摆减振器的设计参数T,C,S相关。下面分析减振器各设计参数对主结构的轴向振动的影响,基于减振器的小幅振动,并以主结构的最大振幅最小作为目标给出离心摆减振器的最优参数。
2.1 无量纲阻尼对幅频响应的影响及其优化
根据文献[8]中无量纲参数的取值范围,这里选取T=0.01,S=0.05, 不同无量纲阻尼下主结构的幅频响应曲线, 如图3所示。
图3中H随β的变化曲线的峰值即为主结构在外激励的作用下共振时的振幅。由图3可知:在C从0.001增加到0.1的过程中, 随着无量纲阻尼的增大, 幅频响应函数的峰值先减小后增大,且峰值点保持向右侧偏,因此,至少存在一个最优无量纲阻尼使得幅频函数的峰值达到可能的最小值[21-22]。且从图3观察到每一条曲线除了都经过(0,1)点,还都经过点Q, 即在点Q处幅频响应H的值与C无关。分析可知当幅频曲线的峰值在Q点时,随无量纲阻尼变化的幅频曲线的峰值达到最小值,此时的无量纲阻尼即为最优无量纲阻尼。为了解析得到最优无量纲阻尼,采用固定点法[23]。将幅频响应函数H写成如下形式:
(11)
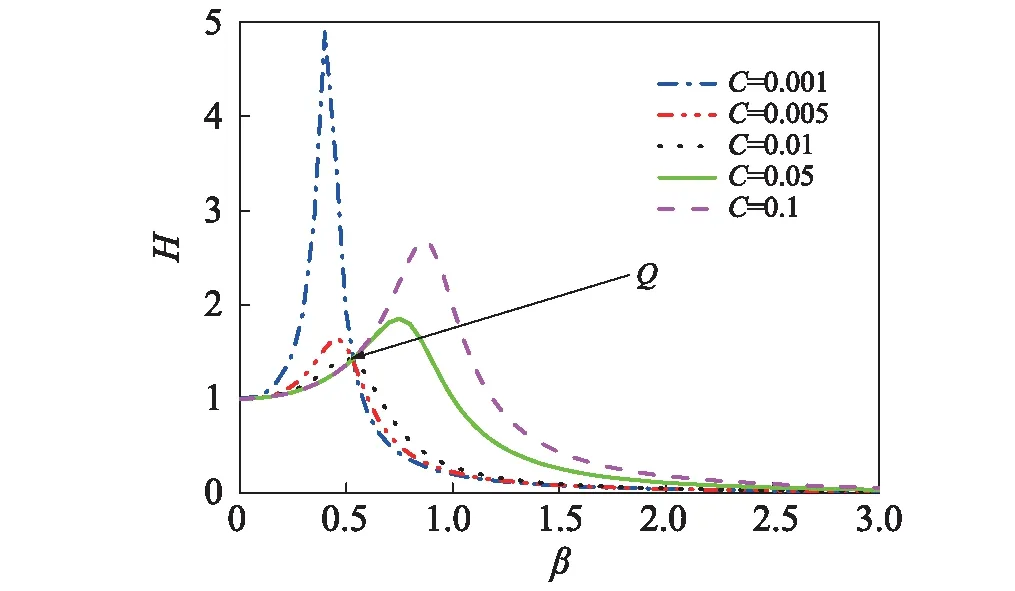
图3 不同C值时主结构轴向振动的幅频曲线(T=0.01, S=0.05)Fig.3 The frequency response function of axial vibration of the shaft with different values of the non-dimensional damping, C and other parameter values: T=0.01, S=0.05
式中:A=1,B=β2T2,E=β4S2+2β4S+β4-2β2S-2β2+1,F=β2(β2ST+β2S+β2T-T)2。
固定点Q的横坐标值可通过A/E=B/F计算得到,记为β0,其值为:
(12)
由式(11)可计算出最优无量纲阻尼为
(13)
把式(12)和式(13)代入式(11)得到最佳无量纲阻尼下的幅频曲线的峰值:
(14)
调谐函数T和质量比S分别取0.01和0.05,最优无量纲阻尼下主结构的轴向振动幅频曲线和摆的转角幅频曲线如图4所示。从图中可以看出当T=0.01,S=0.05,主结构轴向振动的幅频响应曲线幅值的最小值为1.42。
通过上述分析说明,当主结构的参数及离心摆质量及尺寸确定的情况下,要使离心摆减振器达到最佳的减振效果,就须有最佳的无量纲阻尼,其值由式(13)给出。
2.2 质量比对减振效果的影响
由式(14)可知,在最优无量纲阻尼下的幅频曲线的峰值H0与质量比S有关,质量比S对最优无量纲阻尼下的幅频曲线的峰值H0及最优无量纲阻尼的影响如图5所示。
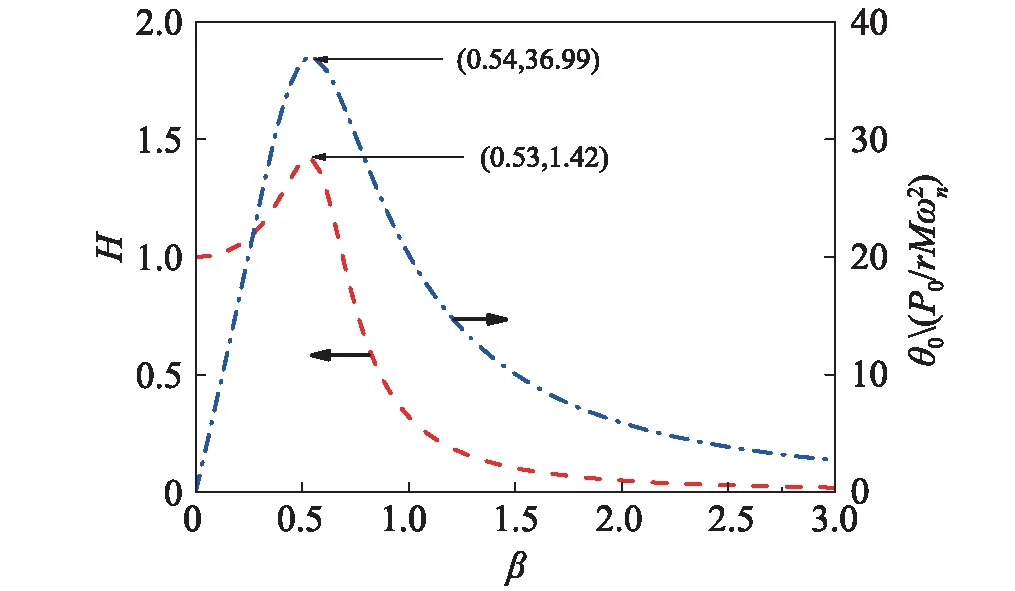
图4 主结构和摆的幅频曲线(T=0.01, S=0.05, C=Copt=0.012 7)Fig.4 The frequency response functions of shaft axial vibration and pendulum rotational vibration with optimal non-dimensional damping, Copt=0.012 7 and other parameter values: T=0.01, S=0.05
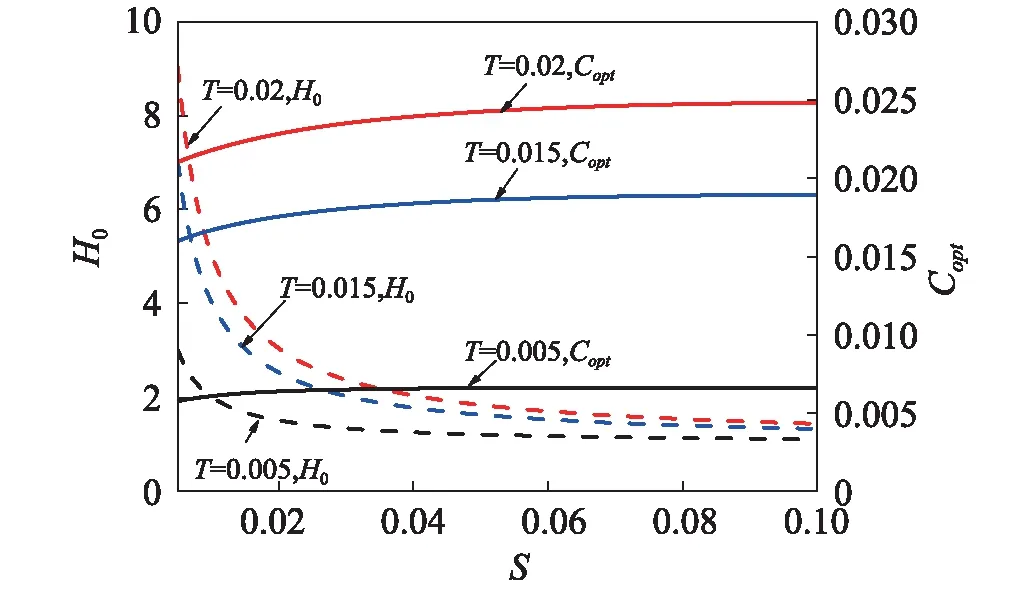
图5 H0和Copt关于S的变化曲线Fig.5 The variations of the resonant amplitude and optimal non-dimensional damping with mass ratio
从图5中可以看出:当调谐函数T给定时,最优无量纲阻尼Copt随着质量比S逐渐增大再趋于稳定,当质量比较小的时候,H0随质量比快速减小,而当质量比增加到一定时,进一步增大质量比并不能有效地增加离心摆减振器的减振效果。
根据式(14),H0关于S求一阶偏导为-2T/S2。可以看出,调谐函数T的正负号不同,峰值H0随质量比S的变化也不同,当调谐函数T>0时,最优无量纲阻尼下的幅频曲线的峰值H0随着质量比S增大逐渐减小,如图5所示;当调谐函数T<0时,最优无量纲阻尼下的幅频曲线的峰值H0随着质量比S增大逐渐增大;当调谐函数T=0时,最优无量纲阻尼下的幅频曲线的峰值H0与质量比S无关。
2.3 调谐函数对减振效果的影响
从上文分析可以看出,当调谐函数T取不同范围时,H0随质量比S的变化关系完全不同,当然T还影响峰值H0。为了研究调谐函数对离心摆减振器减振效果的具体影响,下面将调谐函数T分为T>0,T=0和T<0三种情形分别讨论。
情形一:调谐函数大于零T>0
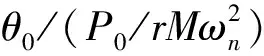
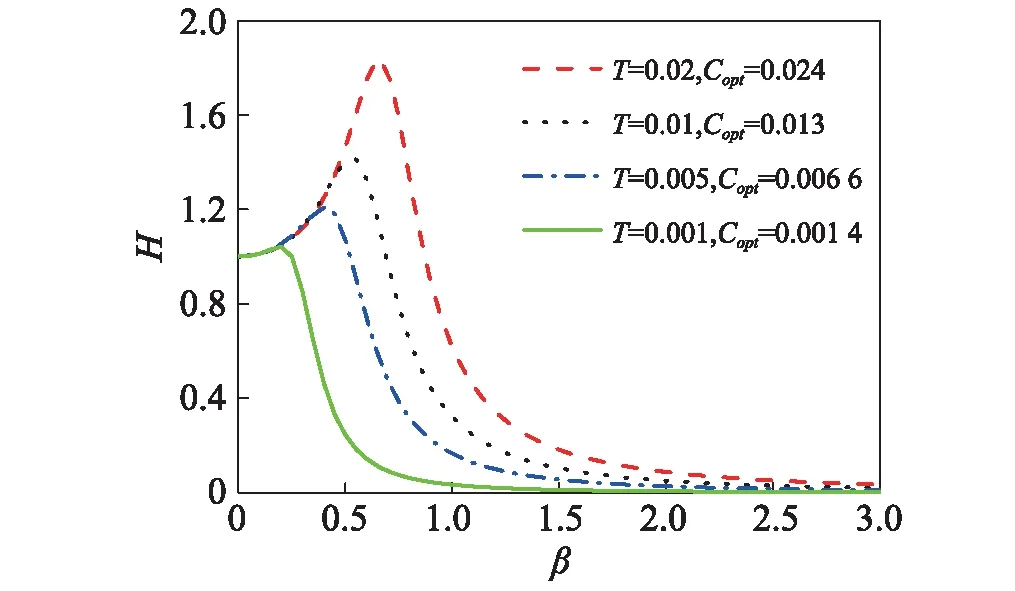
图6 不同调谐函数下的最优无量纲阻尼的主结构幅频曲线(S=0.05, T>0)Fig.6 The frequency response functions of axial vibration of the shaft structure with different tuning functions T>0, the corresponding optimal non-dimensional damping and S=0.05
图7 不同调谐函数下的最优无量纲阻尼的摆的转角幅频曲线(S=0.05, T>0)Fig.7 The frequency response functions of the vibration of the pendulum with different tuning functionsT>0, the corresponding optimal non-dimensional damping and S=0.05
情形二:调谐函数等于零T=0
当T=0时,主结构的幅频响应函数为:
(15)
离心摆减振器的转角振幅如下:
(16)
为求幅频曲线的峰值点,令H关于β的一阶偏导为零,可解得曲线峰值点的横坐标β1为:
(17)
式中:A=-CS2-2CS+
当β=β1时,H取到最大值Hmax为:


图8 不同无量纲阻尼下的主结构幅频曲线(S=0.05, T=0)Fig.8 The frequency response functions of axial vibration of the shaft with different values of the non-dimensional damping, and other parameter values: S=0.05, T=0
情形三:调谐函数小于零T<0
当T<0时,最优无量纲阻尼下的H0关于调谐函数求一阶偏导为:
(19)
为使所取设计参数有物理意义,需满足Copt>0且β0>0,即T<-S(S+1)。以下讨论T<-S/(S+1)这一区间。且由式(19)可以得到当T<-S/(S+1)时,H0随T的增大而减小。

图9 不同无量纲阻尼下的减振器转角幅频曲线(S=0.05, T=0)Fig.9 The frequency response functions of the vibration of the pendulum with different values of the non-dimensional damping, and other parameter values: S=0.05, T=0
当取S=0.05,此时-S/(S+1)=-0.048,T取不同值,最优无量纲阻尼下的主结构幅频曲线及减振器摆角的幅频曲线分别如图10和11所示。从图10中可观察到H0确实随着T增大而减小,且当T=-S/(S+1)时,H=1。当T趋于-S(S+1),减振器摆角相关量的共振幅值很大,可通过调整参数r来达到摆的小幅摆动要求。
综合考虑以上关于调谐函数的三种情况,最优设计是T=-S/(S+1),C=Copt=0,但是这种情况要根据具体工程问题的参数范围来确认离心摆是否作小幅振动,从而确定是否可取。如果以上情况不可取,再考虑T>0的情况。
需要说明的是调谐函数T由表达式(5)给出,除了摆的参数外,还包含了惯容量bθ。一般情况下仅仅通过调整离心摆的结构参数能控制的调谐函数的参数范围较小[8],而且比较困难。本文结合惯容器与离心摆减振器能改善这一不足,通过调整惯容量bθ使得调谐函数的变化范围变得更广,且这样的调整方式能更容易选取合适的调谐函数的值,提升离心摆减振器的减振性能。
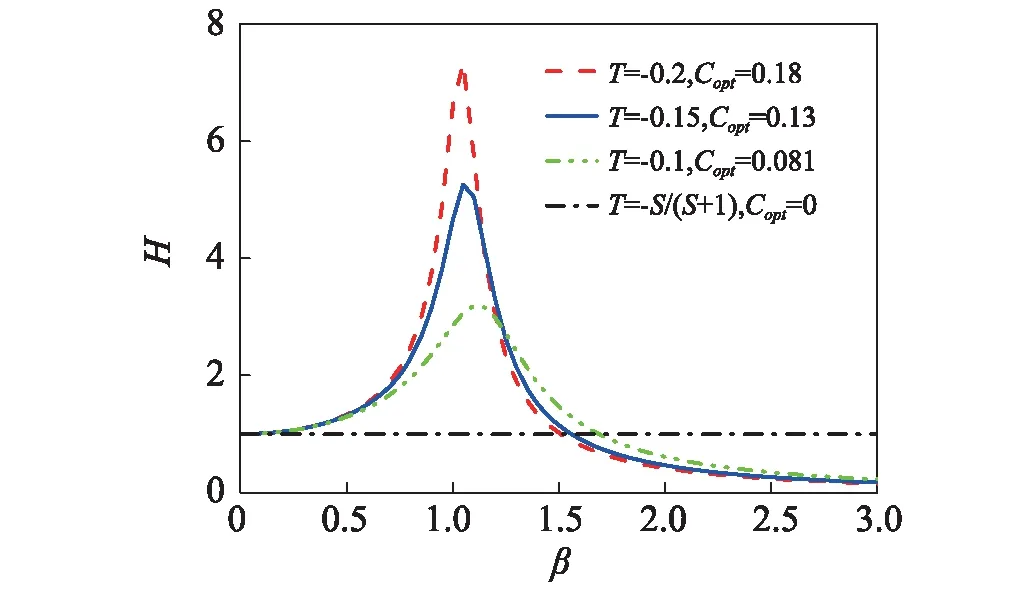
图10 不同调谐函数下的最优无量纲阻尼的主结构幅频曲线(S=0.05, T<0)Fig.10 The frequency response functions of axial vibration of the shaft with different tuning functions T<0, the corresponding optimal non-dimensional damping and S=0.05
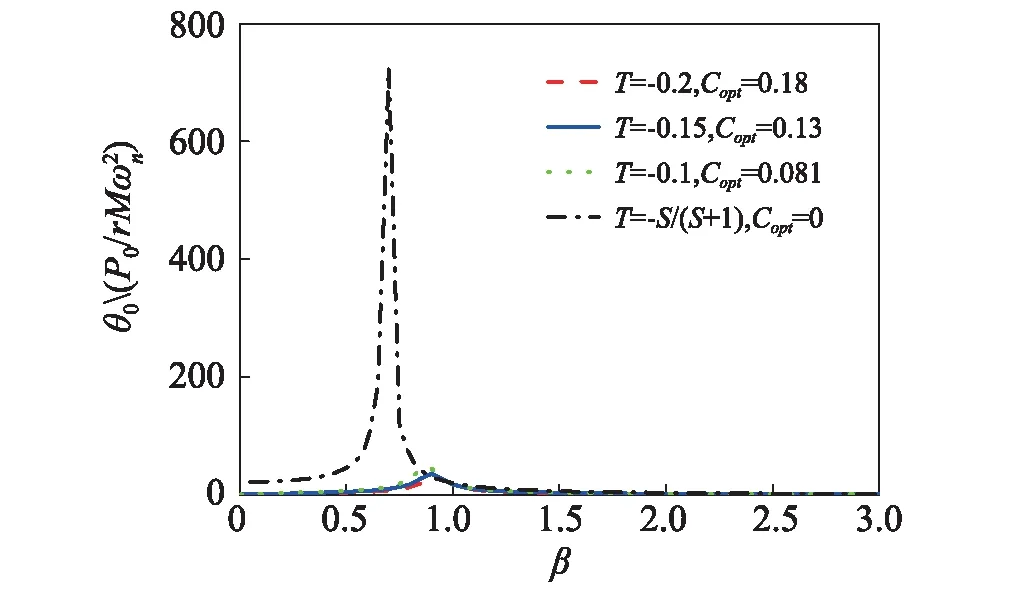
图11 不同调谐函数下的最佳无量纲阻尼的摆的转角幅频曲线(S=0.05, T<0)Fig.11 The frequency response functions of the vibration of the pendulum with different tuning functions T<0, the corresponding optimal non-dimensional damping and S=0.05
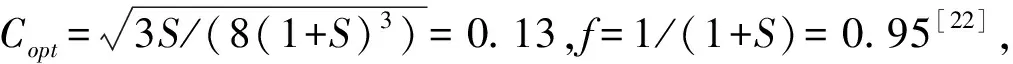
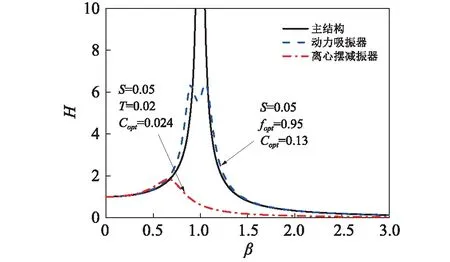
图12 安装不同类型减振器的减振效果Fig.12 The comparison of the absorption effect of DVA and centrifugal pendulum absorber with inerters
3 结 论
本文基于离心摆小幅振动假设,建立了具惯容的离心摆减振器的轴系结构的轴向振动方程,讨论了离心摆减振器的设计参数对主结构轴向振动的幅频响应的影响及以主结构共振幅值最小为目标的参数优化设计。研究发现随着离心摆减振器的阻尼的增大,主结构轴向振动的共振振幅先降低而后增大,即存在一个最优阻尼,并以固定点法给出了离心摆减振器的最优阻尼。调谐函数对主结构轴向振动有很大的影响,对减振器的减振性能也有影响,合适的调谐函数能实现最大的减振效果。惯容的引入可以更方便更容易选取合适的调谐函数的值,只要通过改变惯容量即可实现。最后验证了优化设计后的离心摆减振器用于主结构的轴向振动减振比相同质量比的优化动力吸振器的效果更佳。

