岩石材料动载下泛形裂纹扩展数值模拟
李竟艳, 高文学, 宋肖龙
(北京工业大学 建筑工程学院,北京 100124)
自分形几何建立以来[1-3],分形理论及其应用的研究已经深入到自然科学的各个领域内并取得了瞩目的成就[4-6]。1984年,Manderlbrot等[7]首次实验发现了钢的断裂面具有分形特征,此后其它一些材料断面的分形特性也相继被证实[8-9]。由此分形断裂力学为呈现不规则性、复杂性的岩石类材料断裂研究提供了很好的方法。Xie[10]应用分形几何系统地研究了岩石微观断裂机制、裂纹分形扩展、岩石分形节理力学、岩石分形统计强度理论、分形损伤与分形破碎等一系列岩石力学关键问题。然而,分形应用中面临的无法建立分形裂纹扩展的边值问题及分形裂纹的整数维测度是奇异或者发散的本质困难,严重阻碍了分形断裂力学研究的发展,为避免分形应用中的这一本质困难,Ou等[11]提出了泛形的概念,并在理论上证明了用分形逼近泛形的不合理性。泛形是具有有限层次的自相似(或自仿射)结构,通常可由某种给定生成规则下的有限次迭代产生。此外,对于给定的泛形,一般存在一个与其迭代过程相对应的分形,称其为该泛形的伴随分形,并称伴随分形的维数为该泛形的复杂度,以强调泛形的整数维特征。基于泛形概念,认为自然界的几何是泛形几何而非分形几何,对于自然界中的几何或物理对象用泛形而非分形来描述更加合理,这从根本上避免了上述分形应用的本质困难。由此实现了准静态拉伸载荷下混凝土类脆性材料中泛形裂纹构形的描述,并证实了材料的非均匀性导致泛形断裂面的基本思想[12]。同时,基于泛形有限整数维测度,提出的材料泛形断裂能可作为混凝土断裂性质的表征参数,并为长期以来存在的传统断裂能与临界应变能释放率的计算结果不一致的困惑提供了一个合理的解释[13]。
此外,岩石作为一种天然材料,在采矿作业、地铁隧道、大坝建设等工程领域中,常处在爆炸、冲击等动态载荷环境下。尤其是在动态拉伸载荷作用下,由于岩石材料的拉伸强度远小于压缩强度,常表现为拉伸破坏。因此,对于动态拉伸载荷作用下的岩石动态力学性能以及其动态断裂问题的研究显得尤为重要。借助霍普金森杆试验,学者们对岩石材料在高应变率下的动态拉伸性能进行了一些试验研究[14-16]。但是,由于试验结果很难提供在动载荷作用下岩石材料内部裂纹的萌生、扩展,以及不同加载率下裂纹的汇聚过程,所以很难给出描述岩石动态断裂的定量信息。数值模拟技术则可以作为试验的一个有利补充。但截至目前,动态载荷作用下泛形裂纹扩展数值计算问题还没有相关的研究。本文采用基于扩展有限元的黏聚裂纹模型,对动态拉伸载荷作用下岩石材料的泛形裂纹扩展进行了数值模拟研究,由计盒维数计算给出断面的泛形复杂度。并基于泛形断裂能的计算,从断裂能量释放率的角度探索应变率对泛形裂纹扩展路径及泛形复杂度的影响。研究结果对理解岩石材料动态断裂问题有一定的补充意义。
1 计算模型
岩石类材料内部存在大量缺陷,导致材料性质呈随机分布。为了更好地研究这类材料特性,引入概率统计的方法,即假定组成材料细观各相组成的力学性质满足某种概率统计分布,其中,Weibull分布密度函数较适宜于岩石材料的细观材料特性描述[17]。根据Weibull分布的定义,其分布密度函数为
(1)
式中:w为该分布的分布变量;w0是尺度参数,是一个与平均值E(w)相关的参数,w0与E(w)存在关系E(w)=w0Γ(1+1/m);Γ函数的数值可以通过数学手册查得;m为材料均质度,表征材料的均匀程度。在数值上,首先将计算区域离散为有限单元,所有单元的材料强度满足给定的Weibull分布,不同材料强度的单元数目也应满足该Weibull分布(图1)。进而通过赋值给所有离散单元不同的材料性质来实现Weibull分布。
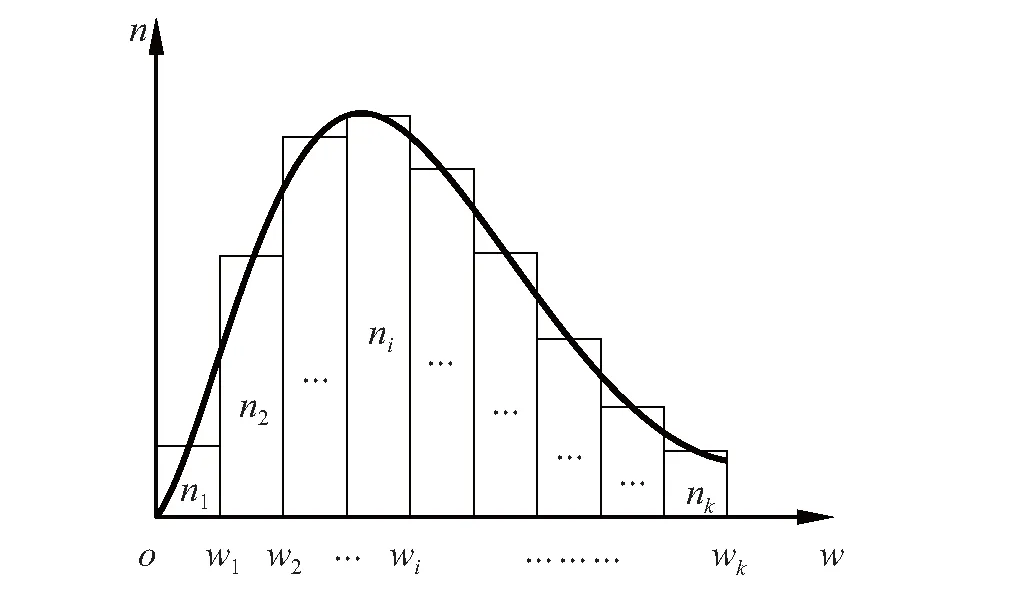
图1 不同强度单元数目的分布直方图Fig.1 Histogram of elements in numerical model with different strength
计算中,应用基于扩展有限元的黏性片段方法(XFEM-based cohesive segments method)。黏性片段扩展特性类似于黏聚裂纹模型。线性损伤起始及演化规律如图2所示。图中,Δn为裂面张开位移矢量,Δnmax为最大张开位移的法向分量,σmax表示最大拉伸强度。裂纹起裂采用最大主应力准则。然而,岩石作为非均匀材料,由于材料属性在空间上分布不均匀,裂纹起裂由应力场及非均匀材料属性的空间分布共同决定,裂纹扩展采用幂指数准则。开裂准则通过用户自定义损伤起始准则(UDMGINI)实现。
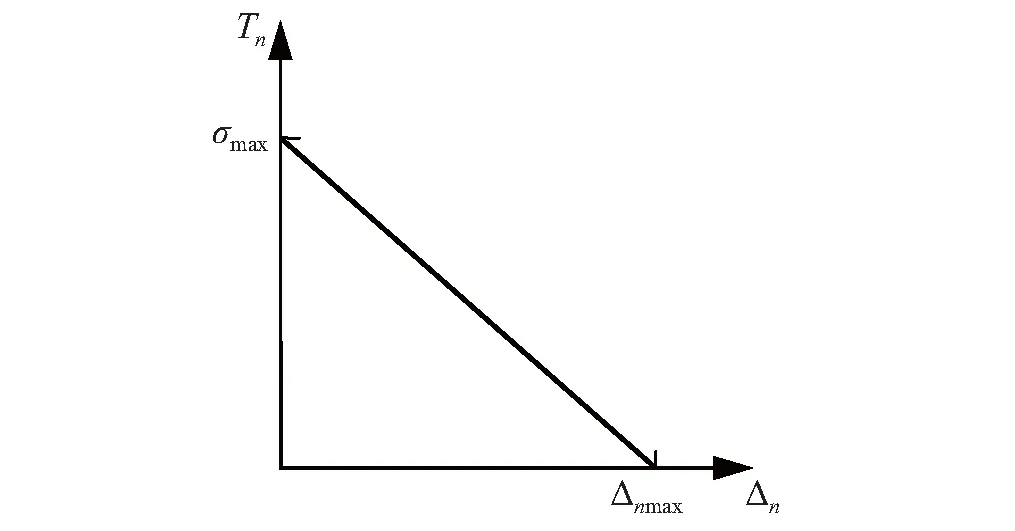
图2 线性损伤演化规律Fig.2 Typical linear traction-separation response
计算模型如图3所示。模型宽L=20 mm,长W=12 mm,初始裂纹长度a=1 mm。计算模型的有限元网格为富集单元。在初始裂纹附近选取边长为50 μm的单元,为了节省计算时间,在远离初始裂纹的区域采用边长为100 μm的单元。以材料拉伸强度ft及断裂韧性Gc作为Weibull分布的非均匀随机空间分布参数,如图4所示,不同的灰度代表了不同的材料属性。模型上下面施加如下速度边界条件
(2)
式中:v为质点速度;tr为载荷上升时间。通过调整选取不同tr值可以方便控制加载率。计算中,在模型左右边界通过无限元技术引入无反射边界条件,防止应力在自由边界处的反射对计算结果的影响。Weibull分布参数为:分布变量拉伸强度的均值E(ft)=3.5 MPa,断裂韧性的均值E(Gc)=0.03 N/mm,均质度m=6。其他的材料参数如表1。

表1 材料参数

图3 计算模型Fig.3 The simulation model

图4 分布变量的空间随机分布Fig.4 Spatial random distribution of parameter in simulation model
2 结果与讨论
当边界速度V=1 m/s 时,根据模型中材料力学参数计算可知,初始时刻一对拉伸应力波以应力约为10 MPa的幅值从模型上下两边向中间传播,如图5(a)所示。根据材料参数可知,大约2.5 μs 后应力到达裂纹尖端并在裂纹尖端处形成应力集中(图5(b))。随着时间增加当该应力幅值达到黏聚模型所设定最大黏聚应力时,裂纹将开始起裂,当裂纹尖端能量释放率达到模型设定材料断裂韧性时,黏聚裂纹面形成,裂纹扩展(图5(c))。裂纹不断扩展,最终达到试件的拉伸失效,得到计算模型的泛形断裂面(图5(d))。某一时刻的裂纹尖端局部放大如图5(e)。
采用计盒维数方法,对模型的泛形裂纹(图5(d))复杂度进行计算。如图6所示,N(δ)为用尺寸为δ的盒子覆盖裂纹构形的最少盒子数目,然后在双对数坐标中用最小二乘法拟合直线,所得直线的斜率即所求复杂度。由此计算得到计算模型泛形裂纹的复杂度C=1.228。从图6可以看出,线性拟合的相关系数R接近1,表明复杂度的计算结果可信度较好。同时岩石类材料分形维数的已有实验结果[9]表明,这类材料的复杂度在1.117~1.523之间。本模型的数值结果落在实验结果区间内,这表明本模型可以用来计算岩石材料中泛形裂纹扩展问题。

图5 泛形裂纹扩展Fig.5 Extension of ubiquitiformal crack
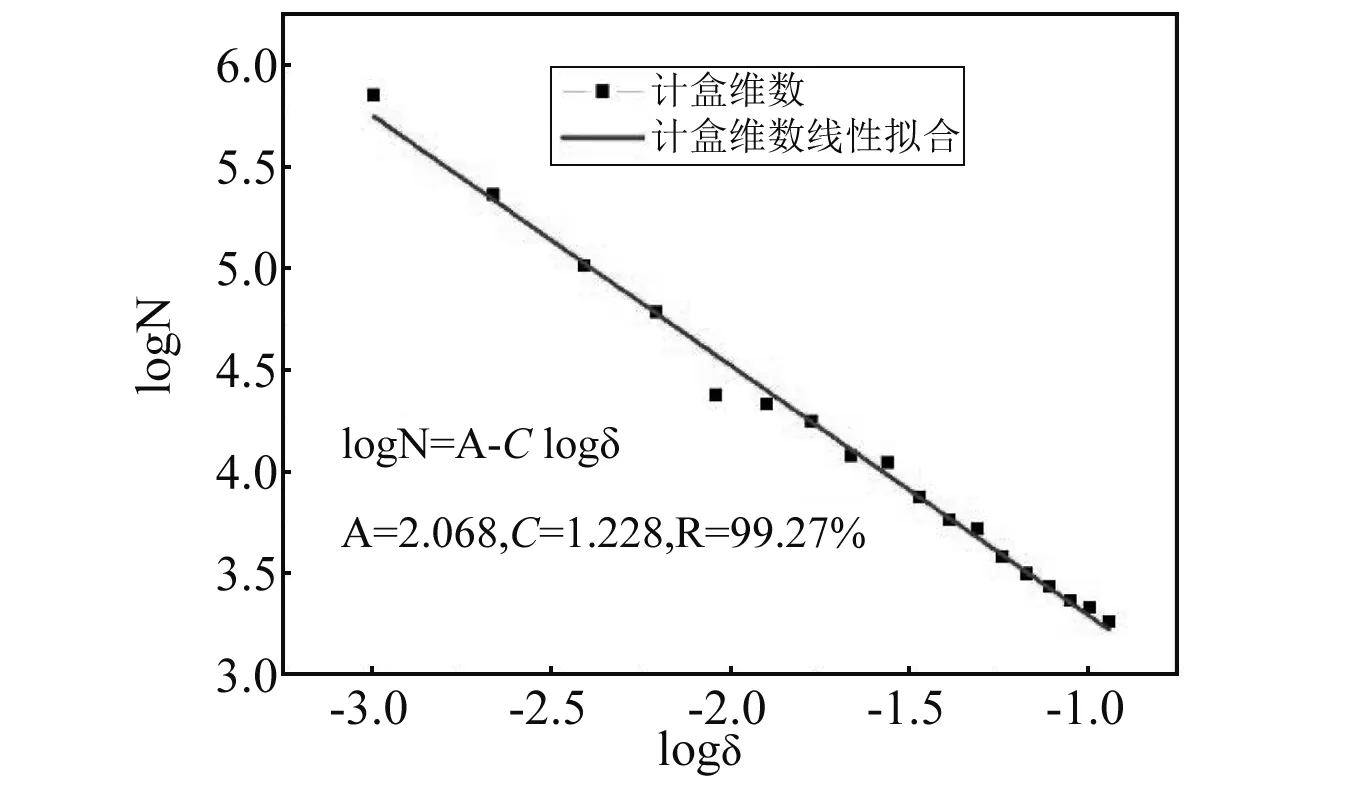
图6 泛形裂纹构形的计盒维数Fig.6 Box counting method applied toubiquitiformalcrack


表2 不同应变率下裂纹的复杂度

图7 不同加载率泛形裂纹扩展路径比较Fig.7 Extension of crack for the different strain rate
从图8分析可知,随着加载率的提高,裂纹扩展的能量释放率增大。从裂纹扩展路径发现,在低加载率下,由于材料性能的非均匀性,能耗较小的单元的能量释放率首先达到断裂韧性,因此裂纹首先发生在断裂韧性较小的单元。但随着外部加载率的逐渐提高,裂纹自相似方向的能量释放率的增加速度远远大于其他的偏折方向,因此裂纹更多沿自相似方向扩展,使得裂纹路径趋于平缓。从物理学观点来看,低应变率或准静态下岩石材料破坏形式主要为单一裂纹沿着断裂韧性最低的路径扩展,但在高应变率下,由于惯性效应的存在,裂纹将没有足够的时间选择断裂韧性相对较低的路径扩展,而是瞬间穿过断裂韧性相对较高的单元,沿自相似方向扩展,从而导致裂纹复杂度降低。以上分析结果表明由于材料性能的非均匀性,导致不同应变率下,裂纹沿不同材料断裂韧性单元扩展,泛形裂纹扩复杂度随应变率增大而减小。

图8 不同应变率下裂纹能量释放率对比Fig.8 Energy release rate for the different strain rate
3 结 论
应用ABAQUS有限元软件对动态拉伸载荷下岩石材料中泛形裂纹扩展进行数值模拟。得到以下结论:
(1) 动态拉伸载荷下岩石材料断裂面为泛形构形,计盒维数计算断裂面复杂度的数值结果与已有的实验结果相符。
(2) 随着加载应变率的提高,裂纹瞬间穿过断裂韧性相对较高的单元,沿自相似方向扩展,从而导致裂纹扩展的能量释放率增大,泛形裂纹复杂度减小。
DOI:10.1007/S00707-017-1859-7.
DOI:10.15632/jtam-pl.55.3.xxx.

