管道环焊缝评估中离散断裂韧性数据的处理*
曹思可,池 强,陈宏远,张骁勇
(1.西安石油大学材料科学与工程学院 陕西 西安 710065;2.中国石油集团工程材料研究院有限公司,石油管材及装备材料服役行为与结构安全国家重点实验室 陕西 西安 710077)
0 引 言
进行长输油气管线建设的最主要环节之一是现场的钢管对接环焊[1]。由于工艺、技术以及现场环境等因素的影响,现场的环焊往往容易产生夹杂、气孔和未熔合等缺陷。在内压和附加外部载荷作用下,缺陷是否会引起管道的断裂,取决于材料断裂韧性的高低。因此断裂韧性数据是环焊缝“合于使用”的工程临界评价(ECA)的重要信息。在管道环焊缝的断裂韧性测试中,为了更加准确地反映所测结构的性能,通常会进行多次试验,但多次试验得到的数据往往是离散的,根据经验筛选数据或取最低值往往会导致不精确或过分保守的结果,这会对工程临界评价的质量造成影响。因此有必要结合相关研究进展及评估标准如API RP 579/ASME FFS-1—2016和BS 7910—2019等[2-4],获得合适的环焊缝断裂韧性数据的处理方法。
本文将依据API RP 579/ASME FFS-1—2016和BS 7910—2019等标准中的相关条款规定,结合数理统计理论,论述3种离散断裂韧性数据处理方法。第1种是对3个以上断裂韧性数据进行简单分析的MOTE(The minimum of three equivalent)方法[5],第2种是用于较多断裂韧性数据处理的分布拟合方法[2],最后1种是评估材料韧脆转变区断裂韧性的主曲线法[6]。
1 MOTE方法
通常情况下测试断裂韧性,最少要进行3次试验,在ECA中使用3次试验的最低值。但对于有些情况,如试验数据不符合要求或者评估需要更可靠的数据,名义上相同的试样需要进行更多试验并获得3个以上有效断裂韧性测试数据。MOTE方法是一些标准和完整性评定指南处理3个以上断裂韧性数据所推荐的1种方法。例如,标准BS 7910—2019和SINTAP工作手册要求,当3次测试结果的最低值小于平均值的70%或者最高值大于平均值的140%时,需进行更多测试,并且建议采用MOTE分析方法[2,7]。
MOTE方法的实质是通过计算获得与3个数据取最低值等效的断裂韧性数据,具体如下。
假设x为断裂韧性数据分布的第50百分位数,根据二项分布概率公式(1)或者(2)可得,3个断裂韧性测试数据有1个或者多个值小于(即不全大于)第50百分位数的概率为87.5%(α=50%,n=3)。即有87.5%的置信度,3个数据的最低值可以保守代表第50百分位数。
(1)
Pr=1-(1-α)n
(2)
式中:Pr为置信度,%;α为百分位数,%;n是试验次数。
根据上述方法,假设n(n≥3)次试验有至少m个数据小于第50百分位数的概率为87.5%,则有87.5%的置信度,n个数据值的第m低值可以保守代表第50百分位数。m的值可以根据公式(3)或者公式(4)求出。
(3)
(4)
为了考察MOTE方法的质量,T Jutla等人[5]对一定样本的断裂韧性试验数据[8]进行了分析,试验次数以3为增量,从3次到30次,每个试验次数通过蒙特卡洛模拟对应取了10组数据并通过公式(3)计算了每组数据取第几低的值与3个数据取最低值等效,结果见表1前两列。由表1可知从6次到30次试验,取第几低的值与3个值取最低值是基本等效的或具有近似安全水平。此外,T Jutla将这些测试数据用于裂纹尖端张开位移(The crack tip opening displacement,CTOD)设计曲线,估计允许裂纹尺寸,并与宽板拉伸试验中相应的临界裂纹尺寸比较,得到了对应的安全系数,分析结果见表1后3列。

表1 小尺度与大尺度试验预测裂纹尺寸的表观安全系数[5,9]
可以看出,取3次试验的最低值、6次试验的第2低值和9次试验的第3低值所得的平均安全系数分别为2.31、3.04和2.74[5]。这表明,6次试验取第2低值或9次试验取第3低值都要比3次试验取最低值产生的结果安全一点。但这种趋势最多观察到15次试验取第5低值,当试验次数高于15次时,如18次试验取第7低值、24次试验取第9低值,得到的平均安全系数将小于取3次试验的最低值得到的。换言之,MOTE方法用于15个以上的试验可能比3个试验取最低值更不安全。
另有一点值得注意,表1中安全系数的标准差会随着样本容量的增大而减少,变异系数(标准差/平均值)也随之减少,这说明样本容量越大,得到的结果越精确。
API RP 579/ASME FFS-1—2016和DNVGL RP F108—2017等标准中都采纳了MOTE方法,并对多次试验取第几低值提出了建议,见表2。
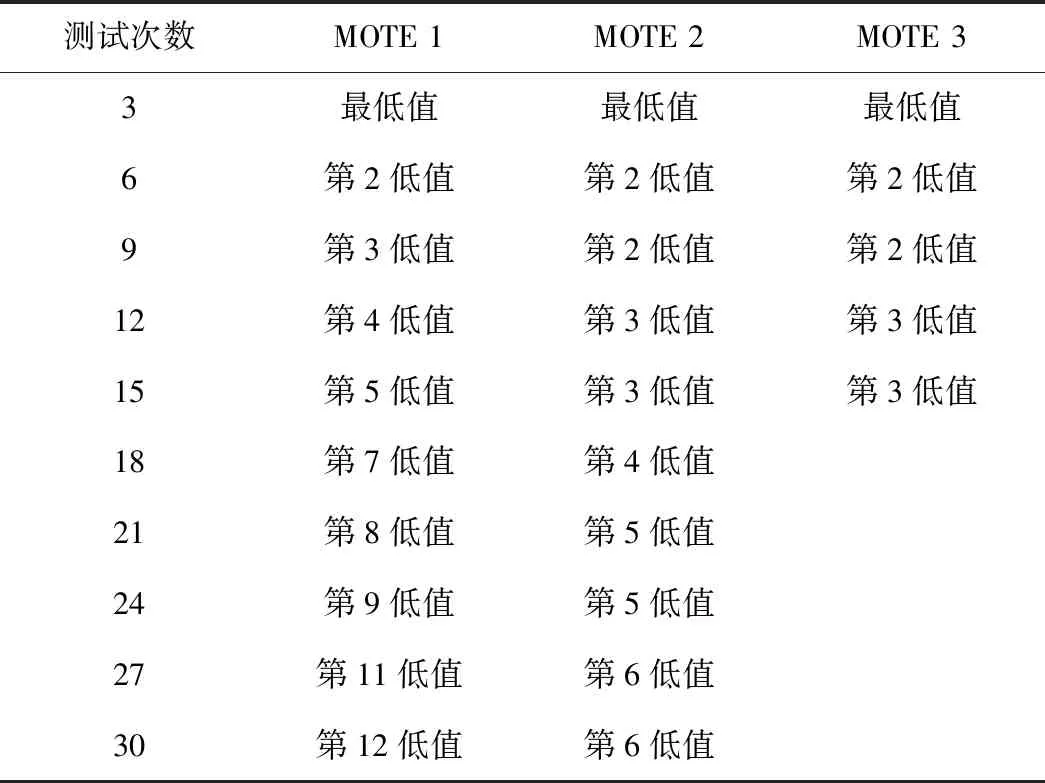
表2 标准中的MOTE方法[9]
MOTE 1是根据公式(3)且令百分位数α等于50%,置信度等于87.5%得出的;MOTE 2是标准API RP 579/ASME FFS-1—2016[6]推荐的方法;MOTE 3为标准BS 7910—2019[2]和DNVGL RP F108—2017[10]相关条款所列方法。由于MOTE方法用于15个以上的等效断裂韧性测试数据可能导致不安全的结果,标准BS 7910—2019在有效数据超过15个时不再允许使用MOTE,并建议使用统计分布拟合的方法[9]。
2 断裂韧性分布拟合
采用少量断裂韧性试验结果,并在工程临界评价(ECA)中使用MOTE方法虽然简单,但是对于完整性要求高的应用场景,可能无法提供足够可靠的结果。使用数理统计方法进行分布拟合能够更好地利用重要的离散数据,提供更可靠的分析[9]。当评估质量要求较高时,一些ECA程序建议测试足够多的试样,以便能够进行断裂韧性数据的分布拟合并能从分布中得到一个特征值(有时为下限值)进行评估。有学者表明,不需要大量的测试就可以对铁素体钢的断裂韧性进行良好的描述,通常10个有效数据也是可行的[11]。国内外很多学者都有使用统计方法来分布拟合断裂韧性数据,但是不同的材料拟合出的分布类型也不尽相同。断裂韧性可能遵循正态、对数正态或威布尔等分布类型。在对断裂韧性数据拟合后,通常需要对拟合优度进行检验,K-S(Kolmogorov-Smirnov)检验和A-D(Anderson-Darling)检验都是常用的非参数检验方法。
有学者对药芯自保护电弧半自动焊(Self-shielded flux-cored arc welding,FCAW-S)焊接获得的X70管线钢环焊接头断裂韧性进行了研究,发现用对数正态分布拟合焊缝的CTOD值比较符合实际数据[12]。另有学者对采用FCAW-S焊接的EH36钢的焊缝及热影响区断裂韧性进行了研究,发现采用正态分布拟合此结构热影响区的CTOD值,相关系数较高,但对于焊缝的CTOD值,用对数正态分布拟合更符合实际数据[13]。Pisarski Henryk等人对MOTE和分布拟合2种方法进行研究,通过对比发现,在分布拟合中选择一个较低的特征值比MOTE方法获得的值更加准确可靠[9]。
此外,国外很多可靠性评估标准也收纳了有关使用分布拟合断裂韧性的方法。例如,标准R6—2014和BS 7910—2019中都有使用拟合分布来分析断裂韧性数据和获取特征值Kmat[2,14]。两种标准的拟合步骤都是相似的,R6—2014的拟合步骤如下:
(5)
式中:Ki是单个试样的断裂韧性值,MPa·m1/2;z为数据点的个数。
2)通过公式(6)求方差S2:
(6)
3)根据公式(7)在给定的置信度下确定Kmat:
(7)
式中:S为标准差,tα是z-1自由度与特定置信水平下累积t分布(Student’s t-distribution)所对应的值,+/-分别给出了置信上限和下限,tα的值可查t分布标准临界值表得到。
BS 7910—2019与R6—2014不同之处在于步骤3,BS 7910—2019采用正态分布单侧公差极限估计90%置信度第20百分位数断裂韧性下限值,如公式(8)所示。
(8)
式中:K0.9为单侧公差极限,其值取决于试验次数。标准BS 7910—2019第7章中已给出1至20次试验K0.9的参考值。
3 主曲线法
3.1 主曲线法简介
铁素体钢和贝氏体钢,通常都具有从低温解理断裂到高温韧性断裂的转变行为。它的特点是与完全延性的上平台和完全脆性的下平台相比,在韧脆转变区断裂韧性有个非常宽的离散带,如图1所示[7]。芬兰VTT研究所Wallin开发的主曲线法是处理这一区间离散断裂韧性数据的先进方法。这个方法的尺寸效应和温度相关性等假设在Wallin后续的研究中都被验证[15]。

图1 铁素体或贝氏体材料的韧脆转变[7]
主曲线法只需少量试验就可以获得整个韧脆转变区内材料断裂韧性的概率分布,其断裂韧性累积失效概率由三参数威布尔分布描述,如公式(9)所示[16]。
(9)
式中:Pf为累积失效概率,%;KJc是临界J积分JC通过公式(10)转化得到的等效断裂韧性,MPa·m1/2;尺度参量K0为Pf=63.2%时断裂韧性KJc的值,MPa·m1/2;Kmin为断裂韧性门槛值,MPa·m1/2。Wallin提出Kmin取20 MPa·m1/2、几何参数定为4[16]。这样,式(9)的三参数Weibull表达式简化为单参数表达式,只要确定某一温度下的K0值,就可以得到此温度下材料的断裂韧性概率分布。Wallin的相关研究表明对于铁素体钢,K0可由公式(11)确定[17]。
(10)
K0=31+77exp[0.019(T-T0)]
(11)
式中:E为弹性模量,MPa;ν为泊松比;T0为参考温度,℃。T0的计算方法将在3.2节中论述。
将公式(11)和Kmin=20 MPa·m1/2带入公式(9),可得:
KJC(Pf)=20+[-ln(1-Pf)][11+77exp(0.019(T-T0)]
(12)
由公式(12)可知,只要确定了参考温度T0便可以获得该材料任意累计失效概率Pf下断裂韧性KJc与温度T的关系曲线,当Pf=50%时,这条曲线即为主曲线。图2是一张主曲线示意图[18],人们通常随主曲线一并给出Pf为95%和5%的曲线,这两个曲线一般分别作为上边界和下边界。令式(12)中Pf=50%,即可得主曲线所对应的公式[3,19]。

图2 主曲线示意图[18]
KJC(med)=30+70exp[0.019(T-T0)]
(13)
式中:中值断裂韧性KJc(med)为Pf=50%时所对应的断裂韧性,MPa·m1/2。
3.2 参考温度T0的计算
参考温度T0为材料中值断裂韧性KJc(med)等于100 MPa·m1/2时所对应的温度,美国标准ASTM E1921—2011[4]对参考温度T0的计算进行了详细描述,T0的计算方法主要有2种,单温度法和多温度法。
3.2.1 单温度法
单温度计算T0,首先要对断裂韧性数据进行检查。当KJc(i)≥Kcen时,KJc(i)被视为无效数据,Kcen可由公式(14)计算。
(14)
式中:B0为韧带尺寸,mm;σys为试验温度下的屈服强度,MPa。
随后将断裂韧性数据根据公式(15)转换为1T(25.4 mm)厚标准试样的等效断裂韧性。
(15)
式中:B为实际试样厚度,mm;B0为标准试样厚度,B0=25.4 mm。
再将等效断裂韧性数据带入公式(16)即可得尺度参数K0,MPa·m1/2。
(16)
式中:r为有效KJc的数量。
最后将所得的K0带入公式(17),再结合公式(18)即可得T0。
(17)
(18)
3.2.2 多温度计算T0
先将试验测得的断裂韧性通过公式(15)转换为1T(25.4 mm)厚标准试样的等效断裂韧性,随后参考温度T0可以由方程(19)的迭代求解:
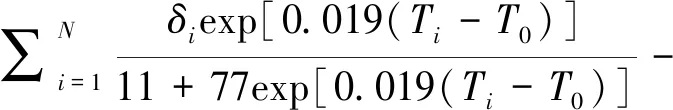
(19)
式中:Ti为KJc(i)的测试温度,℃;δi为检查参数。当KJc(i)大于公式(14)Kcen的值时,δi=0;当KJc(i)小于Kcen的值时,δi=1[4]。
根据一些学者研究,在估算参考温度时,多温度法比单温度法更有效。当使用多温法时,应至少在3个不同温度下测试,并且测试温度越多,所得参考温度T0越准确[20-21]。
3.3 非均匀材料的主曲线分析
主曲线法最初被提出时,仅适用于均质的铁素体钢。实际上,很多材料在宏观上是非均质的,如环焊缝及其热影响区(Heat affected zone,HAZ)。芬兰VTT研究所在SINTAP项目中开发了适用于非均匀材料的最大似然主曲线法(Maximum likelihood-Master curve,MML-MC),该方法可以对非均匀材料断裂韧性进行保守的下限估算,但它不能描述材料断裂韧性较好的部分[6]。为了更好地在非均匀材料断裂韧性评估中使用主曲线法,Wallin等人提出了双峰主曲线法(Bimodal master curve,BMC)。该方法假设材料的断裂韧性数据总体是由两个组合的主曲线分布组成的。材料的累计概率分布Pf可以表示为式(20)形式的双峰分布[22]。
(20)
式中:K01和K02是这两个分布的特征断裂韧性值,MPa·m1/2;Pa是该断裂韧性属于分布1的概率,%。在多温度法评估的情况下,特征断裂韧性(K01和K02)可用参考温度(T01和T02)计算表示。与仅需要确定一个参数的标准主曲线法相比,双峰主曲线分布需要确定3个参数。这意味着拟合的过程更为复杂。为了能够处理多温度下的数据集,必须基于最大似然法,似然函数如式(21)所示。为了简化数值迭代过程,似然函数被转换成对数形式,如式(22)所示[22]。
(21)
(22)
式中:fc是概率密度函数;Sc是生存函数;δ为审查参数。概率密度函数和生存函数表达式分别如式(23)、式(24)所示。
(23)
(24)
一些学者研究认为,双峰主曲线法考虑了材料不均匀性对断裂韧性估算的影响,与标准主曲线方法相比,对材料离散断裂韧性的评估更准确,可以得出稍保守的预测。此外,使用双峰主曲线法通常需要较大的数据集,该方法结果的准确性与数据集大小直接相关[23]。
随着人们对主曲线法的不断研究完善,主曲线法的改进形式也在逐步适用于非均匀材料断裂韧性评估。这在很大程度上拓宽了主曲线法的适用范围和评估质量。
4 结 论
本文针对环焊缝离散断裂韧性数据处理,论述了3种以数理统计为依据的处理方法。结合相关标准对每种方法进行了分析,结论如下:
1)在评估环焊缝的过程中,如果有3个以上的等效断裂韧性测试数据且评估质量要求不高,MOTE是1个简单且有效的处理方法。随着试验次数增加,MOTE方法的结果更加准确,但是过大的样本可能导致MOTE方法的结果不安全,故建议测试数量不超过15个。
2)在等效的断裂韧性测试数据比较多的情况下,可以采取分布拟合参数估计的方法对数据选择性的进行正态、对数正态和威布尔分布拟合并进行拟合优度检验,获取相关度较高的分布拟合,对断裂韧性进行评估或下限估计。通常,从分布拟合中选择1个较低的特征值比MOTE方法获得的值更加准确可靠。
3)当评估材料在韧脆转变区较为离散的断裂韧性数据时,主曲线法是一种先进且有效的方法。热影响区(HAZ)等非均匀材料韧脆转变区的断裂韧性可以采用最大似然主曲线法(MML-MC)进行下限估计,也可以采用双峰主曲线法(BMC)进行整体分析。在使用双峰主曲线法时,由于测试的数量对结果的准确性有直接影响,通常需要较多的断裂韧性数据。

