新型阻尼环对转子-齿轮传动系统弯扭耦合振动的减振研究
王逸龙 , 曹登庆, 杨 洋, 张立伟
(1. 哈尔滨工业大学 航天学院,哈尔滨 150001; 2. 西南交通大学 力学与工程学院,成都 610031;3. 齐齐哈尔二机床(集团)有限责任公司, 黑龙江 齐齐哈尔 161005)
齿轮传动装置经常被用于速度变化或工作方向变化的转子系统中,由于齿轮之间的啮合作用引起的内部和外部激励,导致传动系统极易产生高频噪音,进而降低传动效率,甚至引起整体系统的剧烈振动。这对传动系统的稳定性和可靠性而言非常不利。阻尼环减振降噪技术是改善齿轮振动性能的一个非常有效的措施。通过在齿轮轮毂沟槽内嵌入阻尼环,利用阻尼环与齿轮沟槽间存在的摩擦力消耗系统的振动能量,起到减振降噪的目的[1]。虽然从原理上来看,阻尼环减振技术非常简单,但是阻尼环对齿轮动力学特性的影响却十分复杂。为了避免通过反复的实验来对阻尼环减振技术进行研究,达到减少研究时间和成本的目的,对齿轮-阻尼环系统进行理论分析研究显得非常有意义。
国内外有不少专家学者对阻尼环技术进行了研究并不断的改良,取得了一些成果。但由于阻尼环对齿轮振动的影响十分复杂,到目前为止,大部分的研究工作主要依托实验测试来进行。Okamura等[2]以实验研究为手段,测定了阻尼环结构参数和安装误差对齿轮传动系统的振动噪声所产生的影响。严绍霞等[3]分别以几种不同的工况和不同结构形式阻尼环为变量对齿轮系统噪声谱进行了实验分析,得出了含油双面环的降噪效果最佳的结论。Zucca等[4-6]结合有限元和静态试验研究了不同结构形式阻尼环对航空齿轮动态特性、振动噪声的影响,发现阻尼环可以有效降低齿轮振动位移和减小等效应力波动。在理论分析方面,孙涛等[7]以库伦摩擦力表征阻尼环与齿轮间的摩擦特性,建立了5 自由度的齿轮-阻尼环系统扭转动力学模型。研究了摩擦力对齿轮振动加速度幅值的影响,发现了该系统存在最佳摩擦力,可使得减振效果最佳。于英华等[8]建立了简化的齿轮-阻尼环系统的轴向振动的模型,并由此推导出了齿轮-阻尼环系统振动位移与阻尼环黏滞阻尼之间的关系式,分析了泡沫铝与其他材料相比用于阻尼环减振降噪的优越性。毛炳秋等[9]对两种阻尼材料的力学特性进行了分析,并以阻尼环厚度为变量探讨了阻尼环对齿轮传动振动噪声的影响,发现阻尼环对高频振动噪声的抑制效果尤佳。王庆洋等[10]以于英华建立的模型为基础,建立了齿轮-阻尼环系统的轴向振动的动力学方程组,采用谐波平衡法给出了近似解析解,并通过数值模拟探讨了齿轮-阻尼环系统减振效果与阻尼环参数的关系。彭楠等[11]以C型开口阻尼环为研究对象,建立了安装阻尼环的弧齿锥齿轮传动动力学模型,通过数值模拟给出系统的动态响应,并研究了阻尼环的开口量、厚度和宽度对系统振动特性的影响。冯海生等[12]同样以C型开口干摩擦阻尼环为研究对象,建立了干摩擦阻尼环齿轮传动系统的弯扭轴耦合多体动力学模型,研究了阻尼环结构参数对齿轮传动系统轴向振动特性的影响。
目前有关阻尼环减振特性的研究大多基于干摩擦阻尼环与部件结构之间的摩擦力,这在一定程度上会导致阻尼环的减振效果不佳,影响系统的运动稳定性。为此,本文将探讨一种结合了干摩擦减振器与弹簧减振器的工作原理的新型阻尼环,研究其对转子-齿轮传动系统的减振效果。首先,根据设计的阻尼环-齿轮模型和转子-齿轮传动系统模型,建立阻尼环-转子-齿轮传动系统的弯扭耦合动力学模型,并建立其对应的动力学方程组;通过数值方法求解方程组,以转子的弯曲振动和齿轮的扭转振动所对应的自由度为主要研究对象,对比安装阻尼环前后,这些自由度的共振幅频响应特性,得到新型阻尼环对这些自由度共振时的减振情况;以阻尼器的刚度、阻尼和阻尼环的摩擦力为变量,研究在新型阻尼环的结构参数变化时,系统共振的幅频响应变化规律。
1 安装阻尼环的转子-齿轮系统的动力学建模
本文将以某航空发动机转子试验台装置为基础[13],建立起对应的转子-齿轮转动弯扭耦合动力学模型,并将新型阻尼环安装在该模型中,从而研究阻尼环对该系统的减振效果。该实验设备的内部传动系统由两个传动轴构成,其中低压涡轮盘(转子)所在轴是从动轴,由一个从动轮和两个涡轮盘组成,而主动轴上的齿轮为主动轮,与电机直接通过传动轴连接。对应的转子-齿轮系统在刚性支撑下的模型由图1所示。
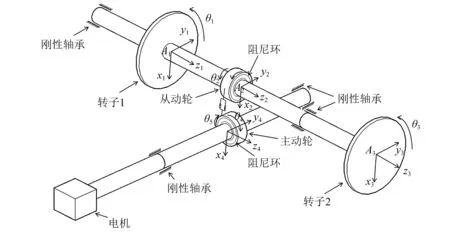
图1 安装阻尼环的转子-齿轮传动系统模型Fig.1 The damping ring-rotor-gear transmission system model
1.1 基本假设
建立安装阻尼环的转子-齿轮传动系统动力学模型的基本假设如下:
(1) 齿轮传动系统的重要内部激励因素包括轮齿时变啮合刚度和啮合误差[14],但为了尽可能地简化模型,本文不考虑时变的啮合刚度,而采用综合啮合刚度来描述齿轮副的激振力传导[15]。
(2) 考虑到扭摆振动对系统的影响较小,为分析方便,本文中忽略扭摆振动。
(3) 由于阻尼环对系统的减振主要通过减少齿轮扭振来实现,虽然转子的涡动也是造成系统弯扭耦合振动的主要原因,但是它并不会影响阻尼环的减振原理,因此本文假设转子都是理想转子,不会发生涡动。
1.2 动力学建模
如图1所示,该模型是一个集中参数三维空间动力学模型,两齿轮用集中质量和集中转动惯量模拟,将传动轴考虑成没有质量但是具有弯曲刚度和扭转刚度的连接体,其质量参数被等效地考虑到转子和转盘的集中质量里,用弹簧和阻尼器来模拟啮合刚度。建立空间直角坐标系Ai(xi,yi,zi)(i=1, 2, 3, 4), 坐标系Ai原点分别位于4个质量块的理想中心,坐标轴xi平行于齿轮啮合线方向(即模型中与啮合刚度方向平行),坐标轴yi垂直于传动轴线方向,而坐标轴zi沿传动轴线方向。设转子1的转角为θ1,从动轮的转角为θ2,转子2的转角为θ3,主动轮的转角为θ4,主动轮上阻尼环的转角为θ5,从动轮上阻尼环的转角为θ6。通过该方法,理论上可以得到18个自由的转子-齿轮传动系统,包括每个质量块的沿xi轴和yi轴方向的弯曲振动、沿zi轴方向的轴向振动,以及沿θi方向的扭转振动。
如图2 所示为安装了新型阻尼环的齿轮模型。该阻尼环模型的安装方式参考了弹簧减振器的工作原理,并结合了阻尼环的减振原理,考虑在阻尼环与齿轮之间设置一种弹簧阻尼材料,用一种中间体(与齿轮用螺栓连接,而与阻尼环仅接触)将两者在扭转方向上关联起来,使两者在扭转方向上不仅存在摩擦力相互作用的关系,还存在弹簧-阻尼力相互作用关系,从而使阻尼环不仅能够发挥摩擦力耗能作用,也能发挥动力减振器的作用[9]。当阻尼环安装在沟槽内后,它们之间的接触压力主要是由阻尼环的弹性变形所造成,根据不同的弹性变形程度,可以对阻尼环与齿轮之间的摩擦力值进行调整。
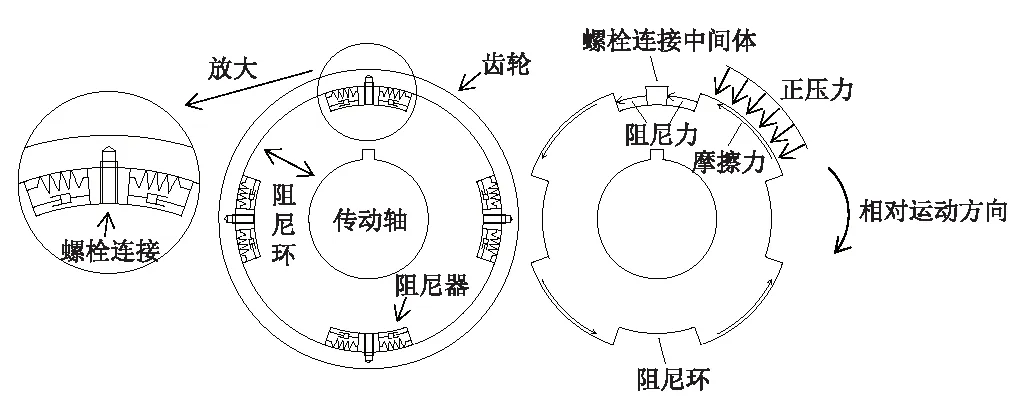
图2 阻尼环-齿轮模型(左图)和阻尼环模型(右图)Fig.2 The damping ring-gear model (left) and the new type damping (right)
根据相关文献[16]可知,齿轮在啮合时,由于传动误差,导致在齿间会产生一个不稳定力,这是齿轮发生强迫振动的主要原因之一。传动误差可以通过傅里叶展开的形式来表达:
e(t)=e0+ersinΩt
(1)
式中:e0为齿轮副之间沿啮合线方向上的传动误差常量(沿xi轴);er为该方向上的传动误差幅值(沿xi轴);Ω为齿轮副的啮合频率,其值为齿轮齿数与转轴转速ω的乘积。
如图3所示,设每个齿轮在啮合处受到的沿xi方向的外力大小为F,沿yi方向的为F′,可以得到:
(2)
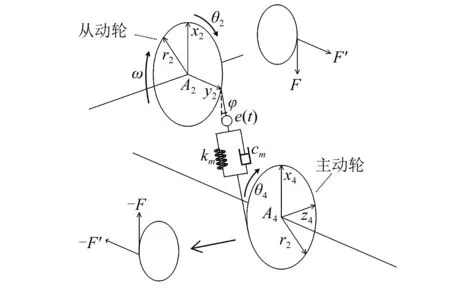
图3 齿轮副受力示意图Fig.2 The gear pair model
由于系统沿yi轴方向的振动量十分微小,该方向上的振动量对啮合力的影响仅仅是通过受力角φ来体现的[12]。设此时只有yi方向存在振动,产生的啮合力为ΔP,s为两齿轮啮合点沿啮合线方向的距离,lxi为沿xi轴上的初始距离,如图4所示。
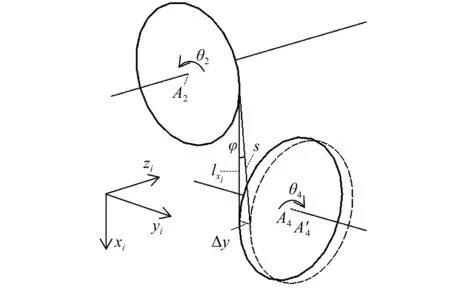
图4 齿轮副方向振动示意图Fig.4 The gear pair’s vibration along the direction
图中:φ是一个与齿轮齿的尺寸、传动误差和沿yi轴方向的振动量等相关的量。由于齿轮尺寸远大于沿yi轴方向的振动量,从而导致φ的值十分微小,即有cosφ≈1, tanφ≈0,因此由式(3)可知:ΔPxi≈0。
(3)
由此可知,沿yi轴方向的振动对系统沿xi轴和扭转方向上振动的影响甚微,可以忽略其耦合作用。为了简化模型,在该模型中,沿yi轴方向的振动被考虑成由一个沿yi轴方向的内激励F′=εF所导致,其中ε为一个比例常数,并且取值非常小。则式(2)可简化成:
(4)
此时,沿yi轴方向的振动就简化成了独立的振动,所以系统的自由度从18变成了14。同理,系统沿zi方向的振动也具有相同的特性,因此可以将系统进一步地从14个自由度简化成10自由度。
结合实际齿轮传动系统中的摩擦特性[4-5, 7-8],本文将采用Coulomb摩擦力模型表征阻尼环与齿轮间的摩擦机理,即:
f=Ffsgn(vr)
(5)
式中:Ff为阻尼环与齿轮间的滑动摩擦力;vr为两者之间的相对速度。
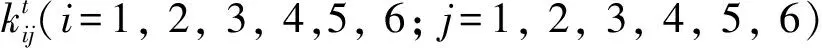
则安装阻尼环的转子-齿轮传动系统的动力学微分方程为:
(6)

2 固有特性和幅频响应分析
由方程(6)可知系统的刚度矩阵和质量矩阵,由此可求出安装新型阻尼环的转子-齿轮传动系统的固有频率和对应的各阶主振型。本文以实际航空发动机转子实验台的构造图纸为基础,借鉴文献[12-13, 15-17]中的主要结构参数,得到系统基本参数如表1所示,然后通过计算得到系统的固有频率,如表2所示。

表1 安装阻尼环的转子-齿轮传动系统基本参数
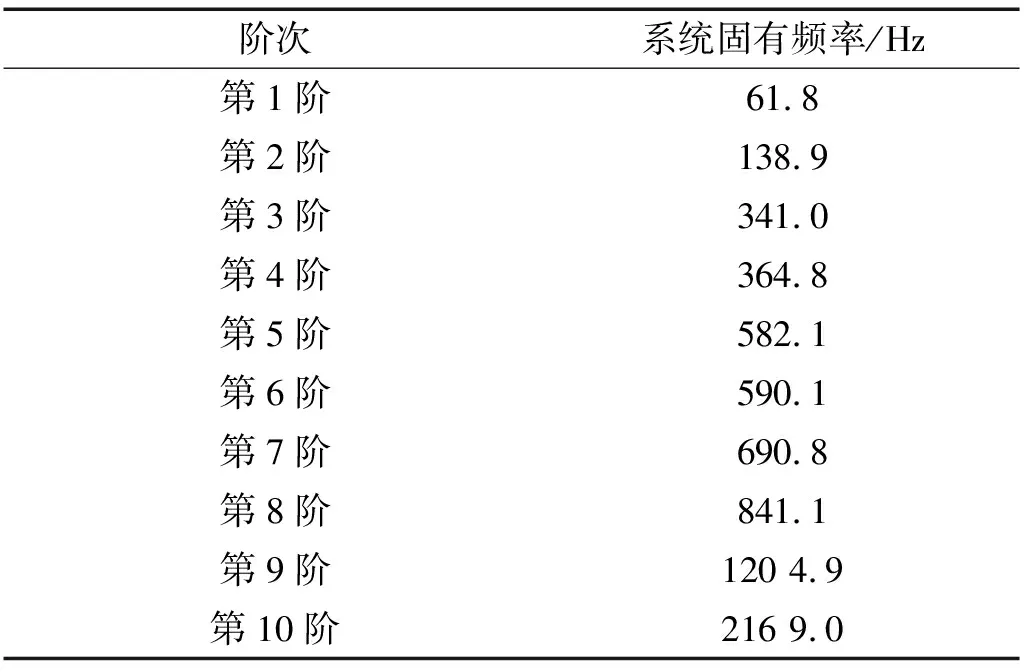
表2 安装阻尼环的转子-齿轮传动系统各阶固有频率
要研究阻尼环对该系统的减振效果,只需要针对该系统的工作环境来进行即可。由于转子试验台的工作转速在2 000~5 000 r/min之间(啮合频率为1 000~2 500 Hz),由表2可知,此区间包含系统的第9、10阶模态。经过归一化处理后,通过系统第9、10阶主振型(如图5所示)可知,系统在这两阶模态附近发生的振动主要是由齿轮的扭振主导。因此,该系统的第9、10阶模态将是本文研究的重点。
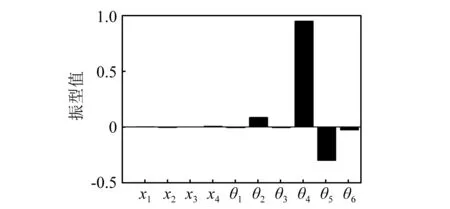
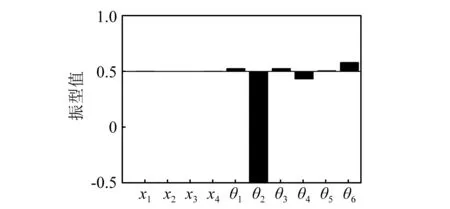
图5 安装阻尼环后系统的第9、10阶模态主振型Fig.5 The No. 9 and No. 10 mode values of the damping ring-rotor-gear system
为了更加直观地研究安装阻尼环对转子-齿轮传动系统的减振效果,需要对安装阻尼环的转子-齿轮传动系统的幅频响应进行计算。为了适应MATLAB中4阶Runge-Kutta变步长数值积分法,在调用ode45函数进行计算时,引入状态变量u(τ),然后将式(6)中的10个二阶微分方程转化为20个一阶状态方程。其中,状态变量u(τ)表示为:
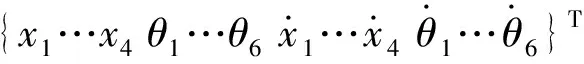
(7)
则方程组(7)可以写成:
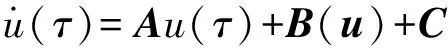
(8)
式中:A为线性系数矩阵,B(u)为非线性项组成的矢量,C为激励项组成的矢量。
尽管,系统在其工作频率范围内发生的振动是由齿轮的扭振所主导,但是由于齿轮扭振所发生的弯曲振动也是不可忽略的。在此,以工程中通常比较关心的几个自由度为主要研究对象,即转子1、2的弯曲振幅和主、从动轮的扭转振幅,设不安装阻尼环时为工况1,安装了新型阻尼环为工况2,而安装了传统不带安装刚度和安装阻尼的阻尼环为工况3(摩擦力与工况2一致),根据表1给出的参数,通过计算系统中这几个自由度在1 000~2 500 Hz范围内的幅频响应,如图6所示,可以直观地看出安装阻尼环后系统的减振情况。
从图6可以看出,系统在共振点附近受新型阻尼环的影响比较明显,这四个自由度的减振率在10%~30%不等,尤其是在第9阶共振点附近时,x1,x3,θ4受阻尼环的影响比较明显,共振幅值分别从17 μm减少到13 μm,4.04 μm减少到3.12 μm,0.017 6 rad(1.01℃)减少到0.014 5 rad(1.01℃),减振率分别为30.24%、29.66%,17.6%。然而,传统阻尼环在相同摩擦力的情况下减振率只有5%左右。由此可看出,新型阻尼环与传统阻尼环相比,对系统在第9、10阶固有频率附近发生的共振有比较明显的减振作用。
综上所述,新型阻尼环对转子-齿轮传动系统在实际工作频率范围内的影响主要集中在系统固有频率附近,而且减振效果比较明显。因此,可知新型阻尼环的作用不仅可以体现在减少齿轮扭转振动方面,还能在高频范围内对复杂的弯扭耦合振动系统进行减振,并且效果较显著,这与文献[9]的结论是相吻合的。
3 阻尼环结构参数对系统共振特性的影响
由上一节可知,阻尼环的加入对系统在工作频率内的弯扭耦合振动影响比较明显。因此,本节将重点分析系统在工作频率内由齿轮扭振所主导的两阶共振。由于阻尼环结构参数的改变会导致与阻尼环扭振相关的模态发生迁跃,从而与表2中的第9、10阶模态发生替换。为了保持对应关系,在此,设表1中第9阶频率对应的一阶为S阶,第10阶频率对应的一阶为L阶。
3.1 阻尼环安装刚度的影响
由于本文的阻尼环的安装方式参考了动力减振器,因此需要研究该安装方式对系统减振的贡献程度。
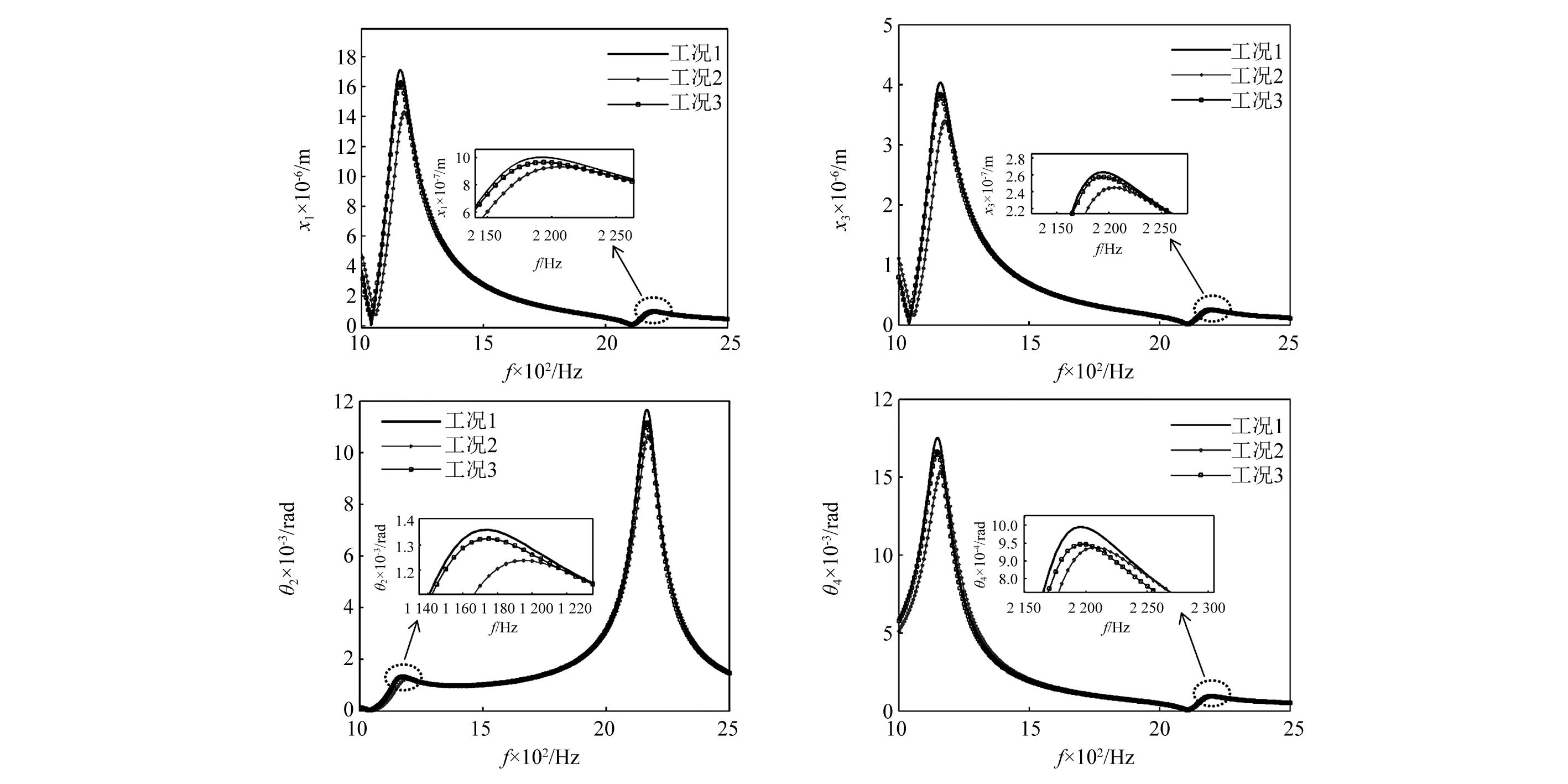
图6 三种工况下x1、x3、θ2、θ4在工作频率范围内的幅频响应曲线Fig.6 Frequency-amplitude characteristic curves for three conditions in the working frequency range (x1, x3, θ2 and θ4)
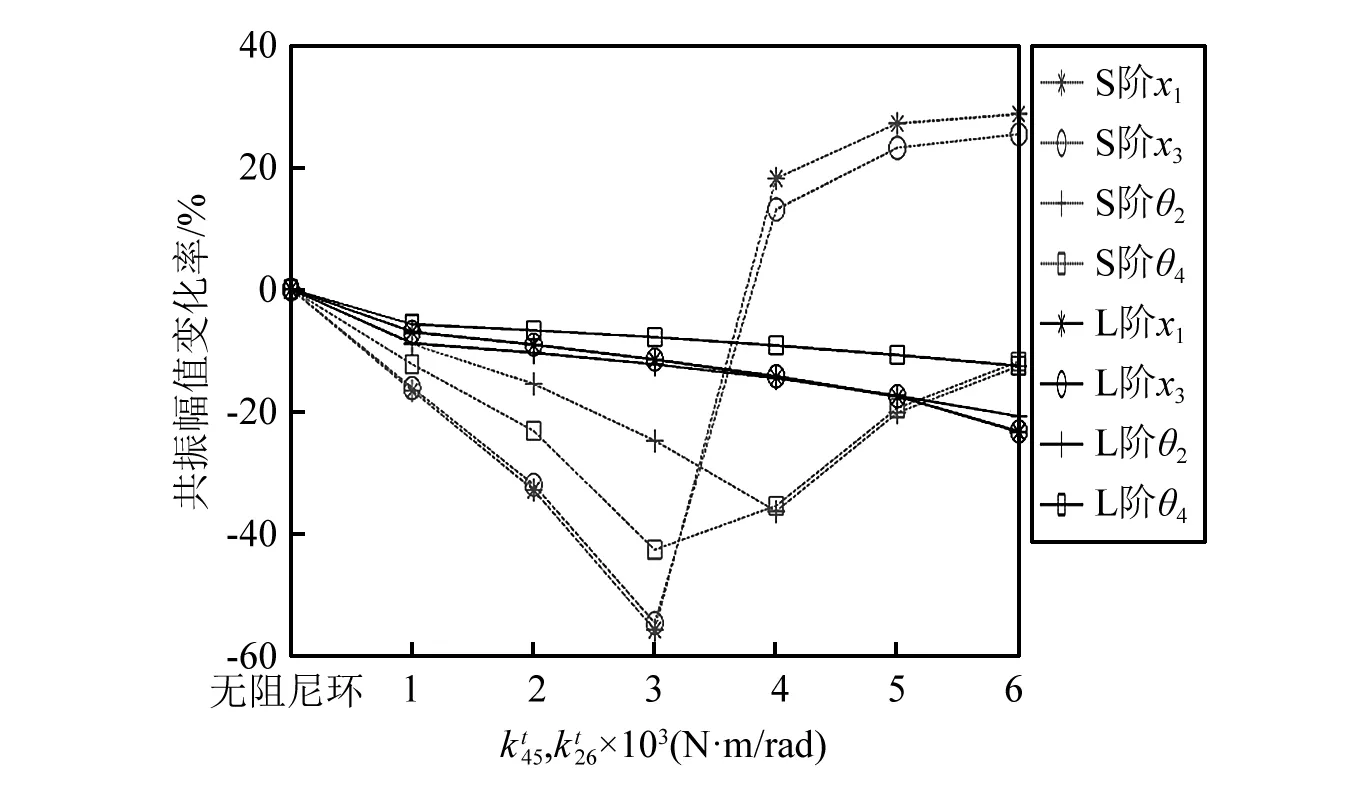
图7 x1, x3, θ2, θ4在S阶和L阶的共振幅值随安装刚度的变化规律Fig.7 The change rate of resonance amplitudes (x1, x3, θ2, θ4) in order S and order L with the increase of
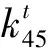
3.2 阻尼环安装阻尼的影响
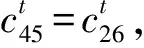
由图8可知,这三阶的共振幅值都随着安装阻尼的增加呈现减小的趋势,这说明安装阻尼的增大在一定范围内是有利于系统减振的。值得指出的是,安装阻尼的增大对S阶共振幅值的影响比L阶的大,即在S 阶时,通过增加安装阻尼的方式可以很有效地减弱系统的振动。但是,这个优势仅仅在安装阻尼相对较大的时候才明显。
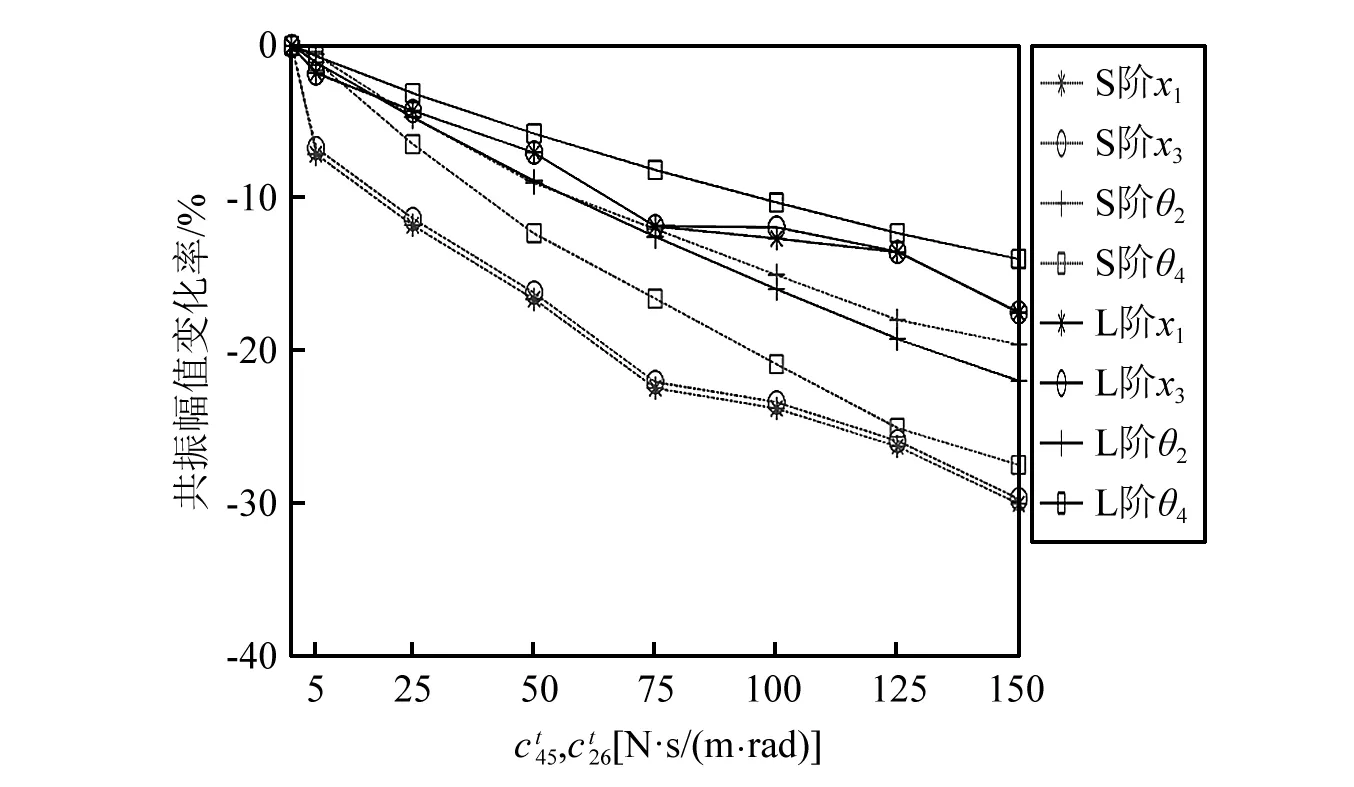
图8 x1, x3, θ2, θ4在S阶和L阶的共振幅值随安装阻尼的变化规律Fig.8 The change rate of resonance amplitudes (x1, x3, θ2, θ4) in order S and order L with the increase of
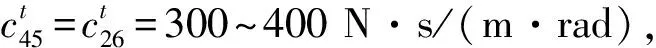
3.3 阻尼环与齿轮之间摩擦力的影响
在对阻尼环的摩擦力对系统减振效果的研究中,大部分学者都是针对简化过的单个齿轮或齿轮副进行研究的,并没有考虑到复杂系统的弯扭耦合振动。由前两节的内容可知,阻尼环的减振作用可以间接地通过减少齿轮的扭转振动来对系统其他自由度的振动带来减振效果。因此,本节将围绕阻尼环与齿轮间的摩擦力对系统各自由度的减振效果进行研究,研究的重点仍然是x1,x3,θ2,θ4这四个自由度的共振。为了方便讨论,设Ff5=Ff6,并分别取Ff5=Ff6=50, 100,150,200, 250, 300时进行计算,同样以无阻尼环时的共振幅值为参考,得到的x1,x3,θ2,θ4随摩擦力变化的共振振幅变化曲线,如图10示。
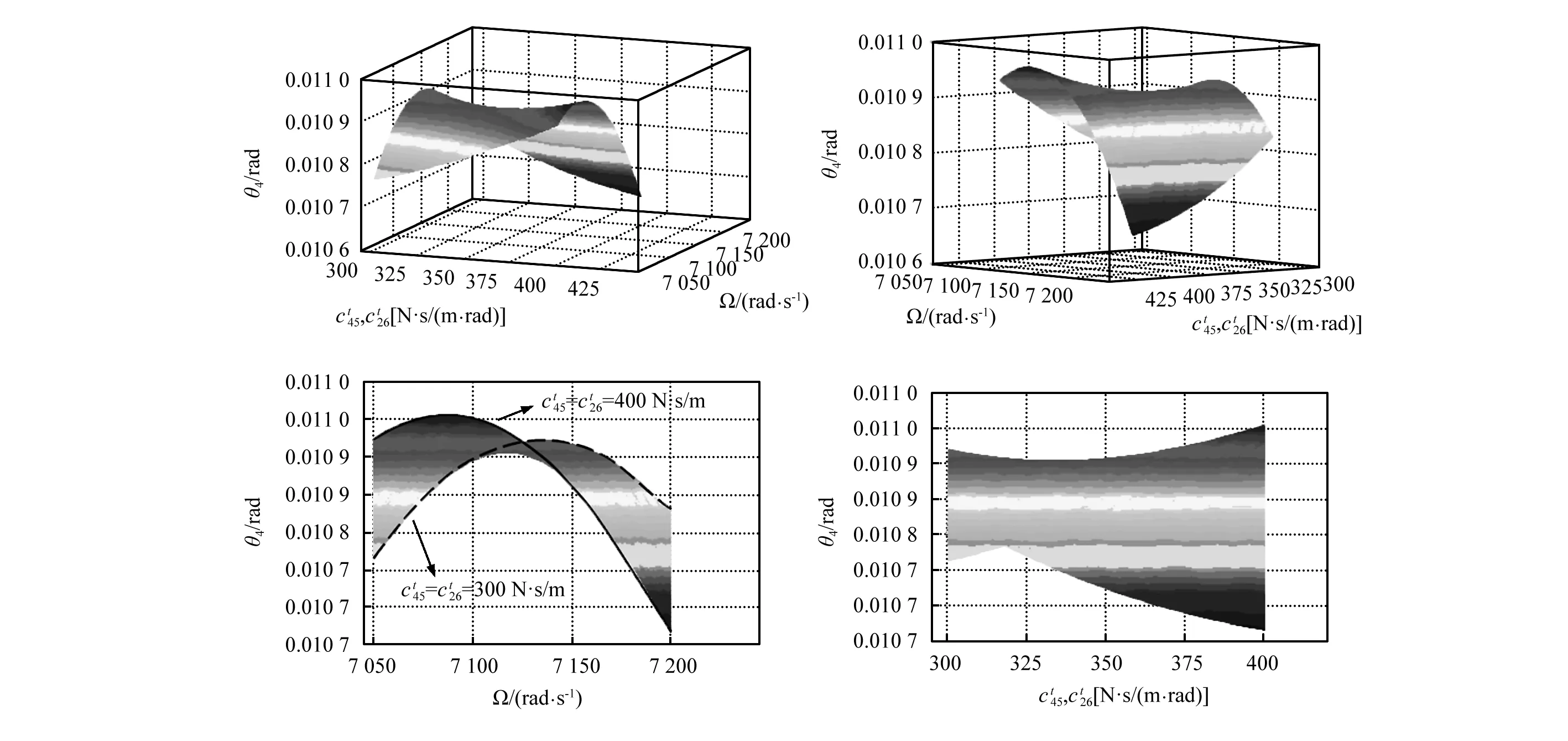
图9 θ4在S阶的共振振幅-啮合频率-安装阻尼关系曲面Fig.9 The surface plot of the relationship among θ4, Ω, in order S
由图10知,尽管随着摩擦力的增加,x1,x3,θ2,θ4在S阶和L阶的减振率变化速度逐渐减小,但从整体来看减振效果较明显,尤其是x1,x3在S阶的减振率,已经达到了30%。这说明,阻尼环的摩擦力对系统的弯扭耦合振动的减振有很明显的贡献。围绕阻尼环与齿轮之间的摩擦力,有很多学者都得出了此间存在最佳摩擦力的结论[8-9]。所以,对于此系统来说,很有可能也存在一系列的最佳摩擦力使得系统各自由度的减振效果最佳,使各自由度的减振效果更好。但是,对于不同的自由度,这个最佳摩擦力一般都不尽相同。在此,考虑到文章篇幅,不再对这些最佳摩擦力进行讨论。
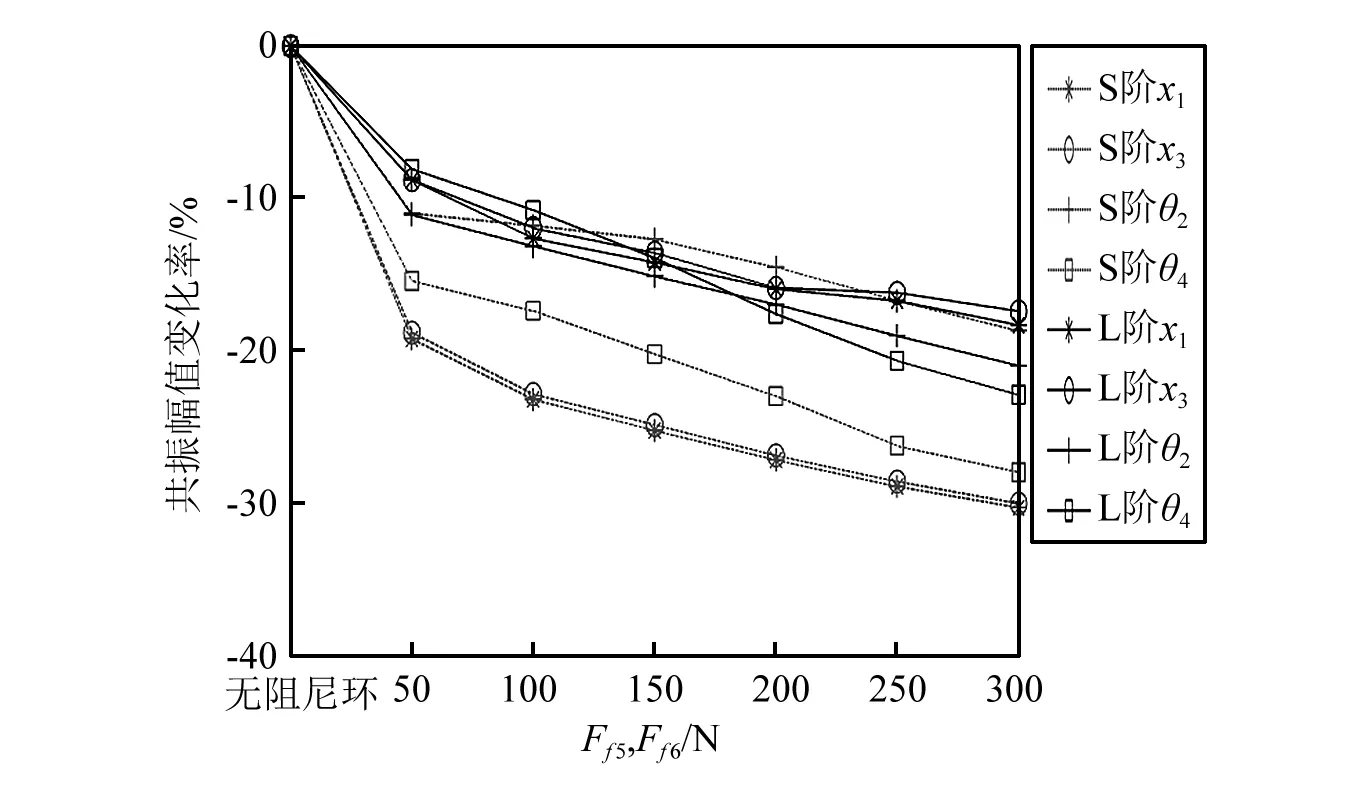
图10 x1, x3, θ2, θ4在S阶和L阶的共振幅值随摩擦力的变化规律Fig.10 The change rate of resonance amplitudes (x1, x3, θ2, θ4) in order S and order L with the increase of Ff5, Ff6
4 结 论
基于动力减振器与干摩擦减振器的工作原理,本文提出了一种新型阻尼环。以某实际的航空发动机转子实验台为研究对象,建立了含新型阻尼环的转子-齿轮传动系统动力学模型。通过数值方法,研究了传动系统的弯扭耦合振动特性,并对比分析有、无阻尼环和安装传统阻尼环情况下的幅频响应特性。在此基础上,进一步讨论新型阻尼环的安装刚度、安装阻尼和摩擦力等参数对工作频率范围内系统共振幅值的影响规律,并得到以下主要结论:
(1)针对转子-齿轮传动系统的高频扭转振动问题,新型阻尼环相比传统阻尼环的减振效果更佳,可有效抑制高频范围内出现的扭转振动,甚至是复杂的弯扭耦合振动。
(2)尽管调整阻尼环的安装刚度可以使其减振效果显著,但是考虑到安装刚度对系统的动力学特性影响较大,在设计阻尼环的安装刚度时,仍需综合考虑转子-齿轮传动系统的具体结构及其工作环境,以获得工作频率范围内的最佳阻尼环参数。
(3)在一定范围内,随着安装阻尼的增加,新型阻尼环对系统各自由度在高频范围的共振起到比较明显的减振作用。并且,对于不同的自由度,各自都存在一个最佳的安装阻尼使得阻尼环的减振效果最佳。
(4)特别强调的是,在高频范围内调整新型阻尼环的摩擦力可有效降低齿轮的扭转振动及其引发的弯扭耦合振动。

