基于一维卷积神经网络的齿轮箱故障诊断

吴春志， 江鹏程, 冯辅周, 陈 汤, 陈祥龙

(陆军装甲兵学院 车辆工程系,北京 100072)

齿轮箱是机械传动系统的关键部件，其广泛应用于风力发电机组、煤矿开采设备、装甲车辆传动机构等很多重要的机械设备。齿轮箱故障可能会造成生产停滞，甚至导致人员伤亡[1]。因此对齿轮箱的实时状态监测与故障诊断就显得至关重要[2]。

现有的实时状态监测大都基于振动信号的频谱分析，在多故障并发，频率耦合，重要频率模糊的情况下，很难进行诊断。而传统的信号处理方法，例如小波包变换(Wavelet Packet Transform, WPT)[3]，EMD分解[4]，提升小波变换(Lifting Wavelet Transform, LWT)[5]等需要人工提取故障特征，再通过模式识别方法，例如人工神经网络(Artificial Neural Network, ANN)[6]、支持向量机(Support Vector Machine, SVM)[7]等进行故障诊断，虽然取得了一定的效果但是难以保证诊断的实时性，而且人工提取的某些特征往往只对特定数据有效，诊断方法难以推广。

作为机器学习的一个重要分支，深度学习近年来借助计算设备的革新已经在各个领域有了广泛的应用[8]。卷积神经网络(Convolutional Neural Network, CNN)是典型的深度学习方法，其最大的优势在于无需人工选取，可以从原始图片中自动学习特征，通过训练调整优化卷积核的参数，实现图片的分类识别[9-10]。

一些专家学者已经将CNN应用到齿轮箱的故障诊断中，并且取得了一定的效果。Chen等[11]通过绘制振动信号的特征统计图作为CNN的输入，实现故障的分类诊断。韩涛等[12-14]将信号做多小波变换和时频变换，以多小波系数图和时频图作为CNN的输入来诊断故障。

然而上述文献利用二维卷积神经网络对振动信号的特征进行学习，没有最大化地发挥深度学习自动学习原始信号特征的优势。

本文提出了一种利用一维卷积神经网络的齿轮箱故障诊断模型，直接以振动信号作为输入，实现端到端的齿轮箱及某型坦克变速箱的故障诊断。与三种传统特征选择加模式识别的方法进行了对比，同时对模型的卷积核大小、CNN层组数等参数的选择做了较深入的分析。

1 典型卷积神经网络结构

CNN是由哺乳动物视觉皮层细胞感受野启发而建立的一种前馈神经网络，现在已经是图片和视频识别领域应用最为广泛的方法。一个传统的CNN模型如图1所示，由一个输入层，两组交替出现的卷积层和池化层，以及全连接层组成。卷积层中每一个特征图都对应一个卷积核，这些卷积核通过一组权重来卷积前一层的输入并组成一组特征输出，成为下一层的输入。与传统滤波器需要人工设定参数不同，卷积神经网络的权值和偏置通过BP算法进行训练。

池化层主要是为了实现两个目的，一是大幅减少输入卷积层的空间维度，使权重参数减少75%，从而降低计算成本。二是控制过拟合，使测试集准确度更接近训练集准确度。主流的池化方式有最大值池化、平均池化、L2-norm池化，本模型采用的是最大值池化。

经过两组卷积层和池化层后，会接一个全连接层。与传统的神经网络类似，全连接层可以应用到不同的分类模型。全连接层后接一个隐藏层，最后由Softmax回归层完成分类。假设有k类的分类问题，Softmax回归的输出可以计算如下[15]:

(1)

式中：W和b分别是权重矩阵和偏置值，O是CNN的最终输出。

图1 典型卷积神经网络结构图Fig.1 Typical convolution neural network structure

区别于传统故障诊断模式，卷积神经网络将特征提取和模式识别过程整合起来，所有的参数都通过BP算法根据输入的训练集数据进行训练，因此模型有较强的鲁棒性和可迁移性。

2 一维卷积神经网络模型

由于振动信号和图片的维度不同，一维的信号最好用一维的模型来解决。因此，本文将图1中所示模型优化为图2所示的一维卷积神经网络模型。优化后的模型由输入层、CNN层组(由卷积层和池化层组成)、全连接层、输出层组成。其中CNN层组可以根据所需分类数据的复杂度增加或减少，本模型使用2个CNN层组。第一个CNN层组中卷积核数量为N1，第二个CNN层组中卷积核数量为N2，相应卷积核的权值向量和偏置值分别为W和b。

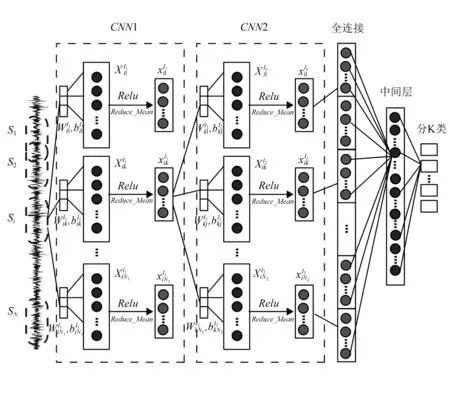
图2 优化后1-DCNN网络结构图Fig.2 Optimized 1-DCNN network structure

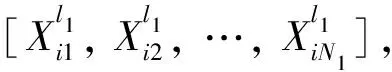
(2)

(3)

(4)

第二个CNN层的输出为：

(5)

卷积神经网络训练的目的是为了使最终的损失达到最小，模型采用的损失函数为交叉熵，优化器选用AdamOptimizer。

3 基于1-DCNN的齿轮箱复合故障诊断

为了证实模型的有效性，本节采用PHM 2009 Challenge Data[16]中小型实验台斜齿轮的复合故障数据和结构更复杂、背景噪声更大的某型坦克的变速器单一及复合故障数据对模型进行对比分析。对一维卷积神经网络模型中卷积核长度、CNN层组数等做了分析。四种诊断模型如图3所示，为了保证对比的公平性，在模式识别部分都采用中间层神经元数量相同的神经网络算法。

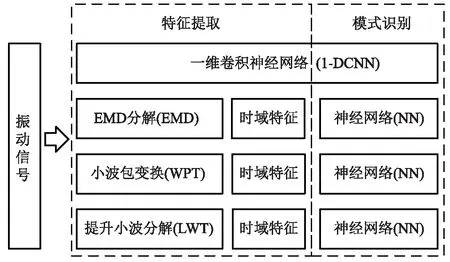
图3 4种故障诊断模型Fig.3 Four kinds of fault diagnosis model

3.1 数据准备

PHM 2009 Challenge Data是PHM协会在2009年国际竞赛的全套齿轮箱数据，包括齿轮、轴承及轴的故障。其实验平台结构如图4所示，内部有三根轴(输入轴IS，中间轴ID，输出轴OS)。实验采用的两组啮合齿轮有直齿轮模式和斜齿轮模式两种啮合模式。箱体两侧分别安装了振动传感器用以采集数据，采样频率为66.67 kHz，采样时间为4 s，采样点数为266 656。

本文以斜齿轮故障为例，斜齿轮啮合模式下共有8种复合故障模式(见表1)，5个工作频率和两种负载状态(低负载和高负载)。为了在充分利用实验数据的同时尽可能提高数据样本组数，每种故障模式包含三种相近转速的数据，采用30 Hz、35 Hz、40 Hz三种转速下低负载通道1的斜齿轮数据对几种模型进行对比。为了优化模型的运算速度，在有限数据样本内包含更多周期的信号，对原信号进行降采样1/3处理。取样本数据段长度为1 600，可以包含2到3周期的振动数据。

降采样后，每隔170点为起点取一组样本，这样每种故障模式就可以得到266 656/3170×3≈1 500组数据样本，其中选900组为训练集，600组为测试集。

图4 齿轮箱结构简图和PHM 2009 Challenge Data实验台结构Fig.4 Schematic of the gearbox and Overview of the gearbox of PHM 2009 Challenge Data

表1 斜齿轮复合故障模式表

3.2 1-DCNN参数选择分析

3.2.1 卷积核长度

卷积神经网络每一层卷积核的数量一般以8的倍数递增，因此第一个CNN层组中卷积核的数量设为8，第二层为16。为了保证训练的稳定性，CNN层组中卷积核长度依次减半。在训练500次后，其长度L与识别准确率P的关系如表2所示。卷积核长度过小识别率较低，而过大又会出现过拟合现象，在考虑不浪费计算资源的情况下，模型选择卷积核长度为23和12。

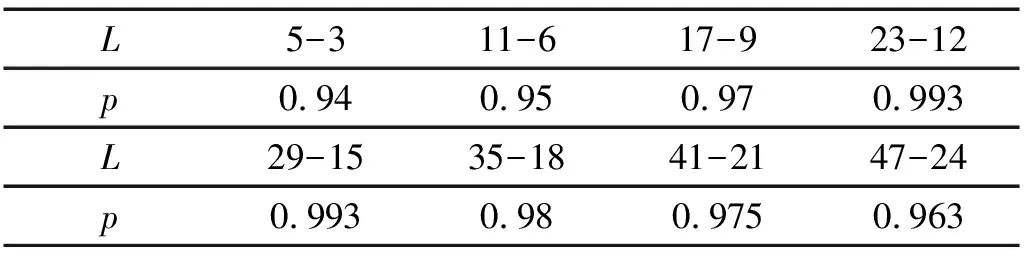
表2 卷积核长度与诊断准确率对照表

3.2.2 CNN层组数量

在对模型进行训练前，需要初始化卷积核的权重向量和偏置，初始化后权重向量呈标准差为0.1的正态分布。训练过程中权值不断更新变化，因此可以通过查看训练后权值向量分布变化来判断所需的CNN层组数量。图5是采用4个CNN层组训练500次后各层组权重出现频次的分布图。第3和第4层组的权重仍近似于初始的正态分布，而且模型准确率没有提升，该层组对诊断模型的贡献度不高，因此只需2个CNN层组。

图5 500次训练后各层权重频次分布图Fig.5 Layers of the weight of the frequency distribution after 500 training

3.3 模型对比

为了尽可能多的提供神经网络输入的特征，首先采用三种不同的信号分解方法对每个样本信号进行多层分解。其中EMD算法分解后取其前8个IMF分量信号；小波包变换采用“db3”对信号进行三层分解，对8个小波包系数重构得到8个分量信号；提升小波分解采用“db3”的提升小波方案进行四层分解，对低频和高频部分分别重建四层近似系数得到8个分量信号。然后对每个样本得到的8个分量信号分别求取峰峰值、标准差、方差、均值、均方根值、峭度、整流平均值、波性因子、峰值因子、峭度因子、脉冲因子、裕度因子等12个时域特征组成长度为96的特征向量，作为神经网络的输入。

每个模型进行500次训练，每次训练更新权重后从测试集中随机选取100组进行测试，得到准确率变化曲线如图6所示(曲线经过smooth函数拟合)。在训练完成后，用全部4 800组测试集数据对模型进行测试。全部测试完成四种模型用时均在3 s左右，平均每组测试时间约为0.6 s。传统模型由于输入数据少，需要训练的参数远小于1-DCNN，因此在模式识别阶段，模型训练时间相对较少，但是数据准备时间及复杂度远大于1-DCNN。多次训练测试后取平均，得到模型的准确率及召回率，如表3所示。准确率表示的是预测为正的样本中有多少是真正的样本，而召回率表示样本中的正例有多少被预测正确了。由图6及表3可以看出，一维卷积神经网络模型的准确率及召回率均高于另外三种模型，而且到达最高准确率所需训练次数更少，到达最高点后准确率波动平稳，模型比较稳健。

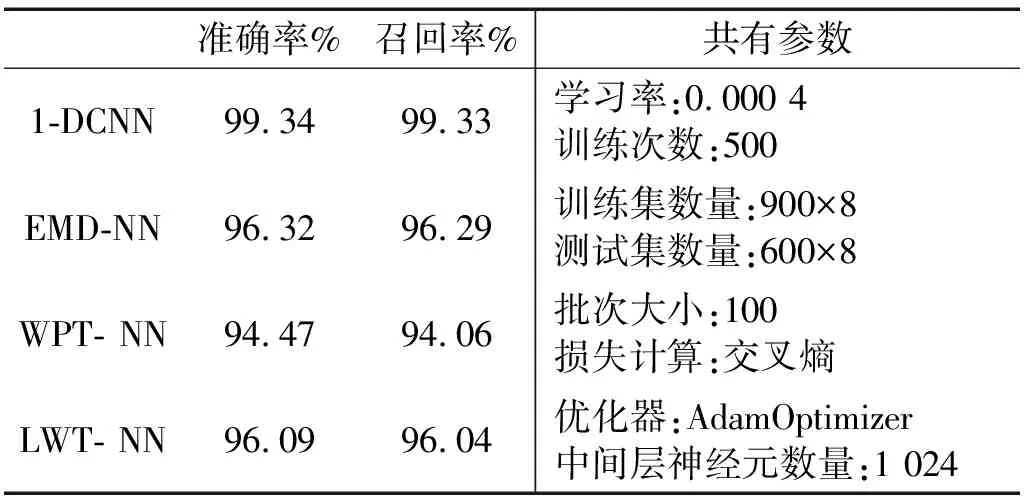
表3 模型测试结果统计及共有参数表

图6 准确率变化图Fig.6 Changes in precision

3.4 变速箱故障诊断

图7(a)为某型坦克变速箱复合故障模拟实验装置，由转速控制台、三相异步电动机、测试平台和电磁测功机组成，变速箱齿轮为渐开线直齿圆柱齿轮。图7(b)和图7(c)为箱体测点位置，选用测点3的三档振动数据为测试数据，测定工况为转速1 000 r/min，负载150 N·m，采样频率20 kHz。

图7 实验台整体结构, 箱体测点示意位置和箱体测点实际位置Fig.7 Overview of the experimental platform, Schematic diagram of test points and actual location of test points

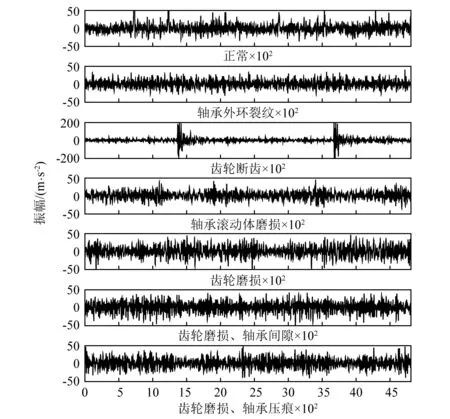
图8 故障设置及时域信号图Fig.8 Fault settings and time domain signal diagram

样本数据长度取略多于两倍整周期的2 400点，故障设置及时域信号如图8所示。可以看出，除了断齿故障可以明显区分外，其余故障很难在时域图中甄别，尤其是后三个齿轮磨损及齿轮磨损和轴承的复合故障，更是难以区分。因此，在诊断复合故障时，1-DCNN将CNN层组增加为3个，而诊断单一故障时仍为2个。

实验进行两组测试，测试一：考虑前5个单一故障的诊断；测试二：考虑5个单一故障及2个复合故障的诊断。最终诊断结果如表4所示，1-DCNN在诊断单一和复合故障时都取得了很高的准确率，而另外三种模型在诊断复合故障时准确率有所下降。准确率变化如图9和图10所示，两次测试WPT-NN和LWT-NN的准确率波动变化较大，而1-DCNN训练过程表现都很稳定，在250次左右达到最高值。说明通过调整CNN层组数量，1-DCNN模型对复杂信号分类诊断具有很好的泛化性。

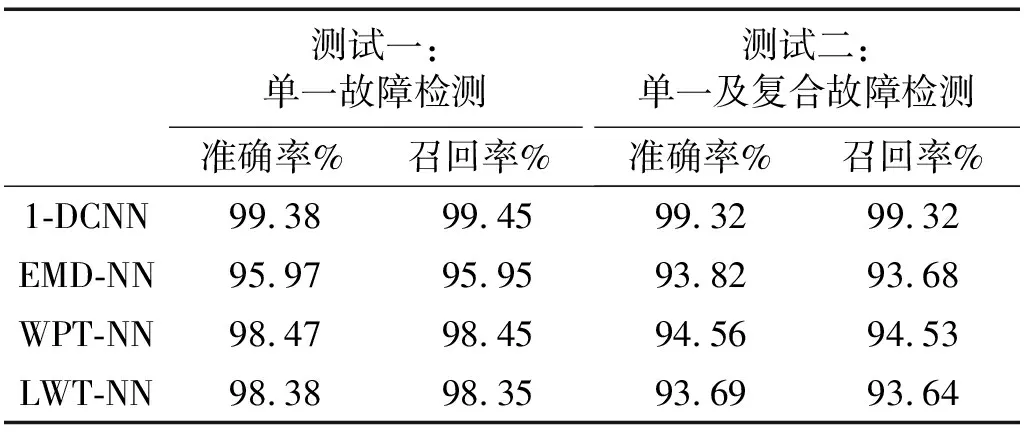
表4 两次测试结果统计表

图9 测试一准确率变化图Fig.9 The precision of the first test change

图10 测试二准确率变化图Fig.10 The precision of the second test changes

4 结 论

本文提出了一种利用一维卷积神经网络的齿轮箱复合诊断模型，可以直接从原始振动信号中自动学习特征完成分类诊断。采用PHM 2009 Challenge Data斜齿轮复合故障和某型坦克变速箱单一及复合故障对1-DCNN以及传统的EMD-NN、WPT- NN、LWT- NN诊断模型进行了三次测试，实验结果表明：

(1) 训练好的1-DCNN模型可以使用采集到的振动信号直接作为输入，诊断的时间短，真正实现了端到端的快速故障诊断。

(2) 三次测试1-DCNN均取得了99.3%左右的准确率，高于另外三种模型。由于测试数据来源既有小型齿轮箱，又有结构更为复杂，噪声干扰更为严重的实装变速箱，说明1-DCNN有很高的泛化能力。对于诊断难度更大的变速箱复合故障，通过增加CNN层组数量，依然能得到较高的准确率，说明模型的可塑性较强。