包覆铝合金变形抗力模型研究

李晓娜，谢满堂

以Al-Mn-X系合金为芯材、双面包覆Al-Si-X系钎料合金的三层复合包覆铝合金带材，不仅具有芯材合金良好的加工性能和耐腐蚀性能，且由皮材在热交换器钎焊过程中直接提供钎料，简化工艺、降低成本、操作方便，广泛地应用在各种汽车热交换器领域之中，是制造管带钎焊式热交换器的重要材料之一[1-3]。热轧复合法是目前生产三层复合包覆铝合金带材的成熟方法，它利用轧制压力破坏芯材与皮材待复合表面的氧化膜和污染膜等，裸露出新鲜表面，然后在一定条件下，将芯材与皮材界面复合在一起。包覆率是指单面钎料包覆层厚度占总厚的百分比。当包覆率较小时，因钎料供应不足，会造成虚焊或假焊，钎焊质量差，导致产品报废；包覆率较大时，因融熔钎料流动过快，使复合箔高温抗下垂性变差，又会导致复合箔坍塌。可见包覆率对复合铝合金带材的综合性能有直接的影响。因此，国内外的有关标准均对钎焊料的包覆率作出严格规定，要求在满足钎焊性能的前提下，包覆率的波动范围应控制在±2%以内。由于热轧复合过程是影响包覆率变化的主要环节，所以研究热轧复合过程中包覆率的变化规律，建立精确实用数学模型，对于实际生产有重要指导意义。

包覆铝合金所用的芯材为3003，皮材为4004。对比其他生产方法，包覆铝合金的热轧生产方法更高效也更经济，然而包覆铝合金热轧过程中的塑性变形非常复杂，很难建立准确的数学模型。国际和国内与此相关论文很少，而本文是通过热压缩试验先拟合出铝合金3003和4004的变形抗力模型，然后再基于试验结果对包覆铝合金进行热压缩仿真有限元分析后提出一种适用于包覆铝合金热轧过程的变形抗力模型。

1 铝合金变形抗力模型

包覆铝合金材料是4004/3003/4004复合材料，需要先通过热模拟试验得到3003和4004铝合金的周纪华变形抗力模型[4]（见式1），用热压缩方法在Gleeble-1500热模拟试验机上测定材料的变形抗力。为消除端面摩擦对变形抗力的影响，得到单向压应力，在Ø8 mm×12 mm圆柱体试样上、下端面各车0．2mm深的凹槽，并在凹槽中填充润滑剂（75%石墨+20%机油+5%硝酸三甲苯酯）。采用电阻加热升温，加热速率为10℃/s，分别加热至200℃，300℃，400℃，450℃，500℃后均保温5 min，然后进行变形程度为60%压缩变形，变形速率取 0．1s－1、1 s－1、5s－1、10 s－1、20 s－1、50 s－1，变形后立即水淬，由计算机自动采集真应力、真应变、压力、位移、温度、时间等试验数据，通过统计分析软件SPSS对周纪华变形抗力模型进行多元非线性回归分析,得出模型中系数a1～a6，最后得到铝合金3003和4004的变形抗力模型（见式2、式3）。

式中，σ—变形抗力（MPa）；σ0—基准变形抗力，即t=300℃、和时的变形抗力（MPa）；T=t/300；t—变形温度（℃）；ε˙—变形速率（s－1）；ε—变形程度，a1～a6—回归系数。

2 包覆铝合金热压缩仿真分析

2.1 仿真模型

针对包覆铝合金的轧制过程，忽略展宽影响，采用DEFORM－2D进行热压缩仿真（见图1），样品为30 mm×30×mm 15 mm方形体，包覆率为20%，即三层铝材的厚度分别为3 mm、9 mm、3 mm。为了得到不同的基准应力值分别取五种不同温度（200℃，300℃，400℃，450℃，500℃），六种不同应变速率 (0．1 s－1、1 s－1、5 s－1、10 s－1、20 s－1、50 s－1) 和七种不同的包覆率 （13．3%，16．7%，20%，23．3%，26．7%，30%，33．3%） 进行模拟仿真。

图1 包覆铝合金热压缩仿真二维模型

2.2 包覆铝合金流变应力曲线

试验后先得到不同应变速率下真应力－真应变曲线（见图2），从图中可以看出，随着温度降低和应变速率提高，变形抗力也有所增加。并且在同样条件下，包覆铝合金的变形抗力维持在铝合金3003和4004的变形抗力之间。只有在高应变速率下，在200℃时的仿真曲线先是略有下降，最后趋向平缓，究其原因是高应变速率会使包覆铝变形抗力较小的芯板3003铝合金更容易变形，导致三层铝材总变形抗力有所下降，等到两种材料被均匀压缩后，综合变形抗力逐渐趋向平缓。而在高温情况下，所有变形抗力都将随应变的增加而增大，这是因为三层板材之间的摩擦力导致金属横向流动受阻，压头的压力增加，从而导致变形抗力上升。

2.3 变形抗力模型回归

通过统计分析软件SPSS对仿真数据进行非线性回归后得到包覆铝合金基准变形抗力为129．529 MPa时的回归结果（见表1）。

将回归所得模型系数代入式（1），即可得到包覆率为20%的包覆铝合金的变形抗力周纪华模型：

2.4 变形抗力模型修正

在考虑到包覆率对包覆铝合金变形抗力的影响后，提出以下修正模型：

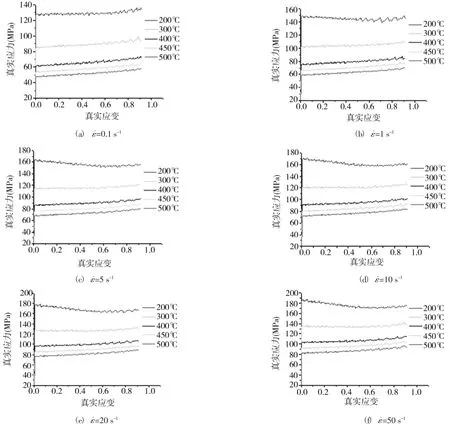
图2 不同应变速率下的真应力-真应变

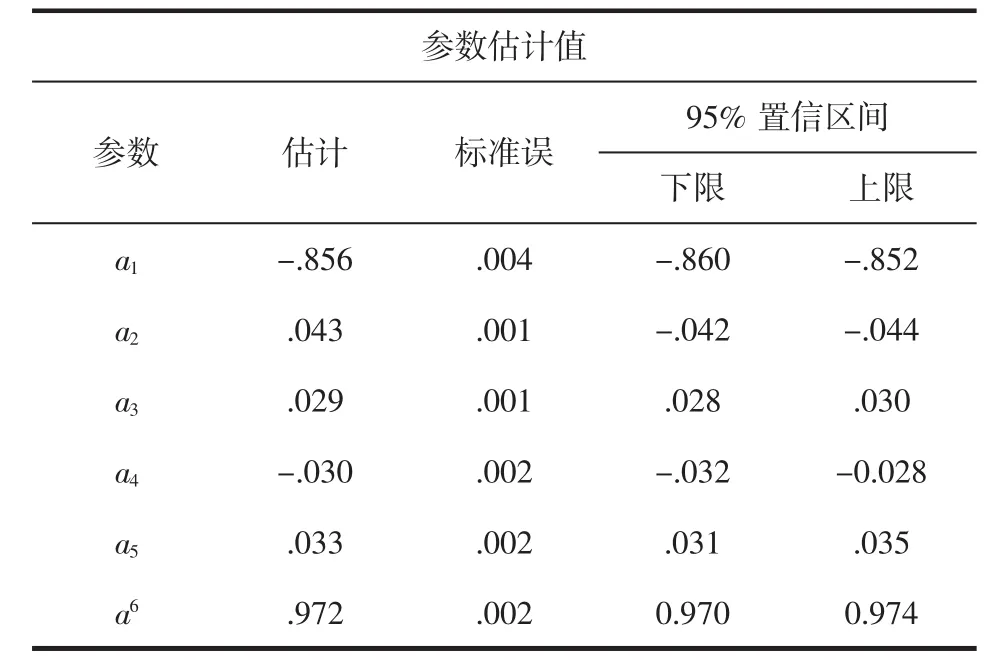
表1 包覆铝变形抗力模型系数回归

式中，a—回归系数，与包覆率有关；σ0—不同包覆率下包覆铝板的基准应力值。此处为即在300℃，应变速率10 s－1，压缩量为20%时的应力值，其大小与包覆率以及两种材料的基准变形抗力有关，即

式中，c—与包覆率有关的系数。

将通过仿真得到不同包覆率包覆铝合金的基准应力值数据 （见表2） 以及 σ3003、σ4004代入式（6），即可得到c与包覆率b的关系式：

表2 不同包覆率包覆铝板的基准变形抗力值

通过线性拟合得到的式（7）能准确反映系数c与包覆率b的关系（见图3）。

综合式 (5)～式 (7)，即可得出包覆铝合金的基准变形抗力修正模型：

图3 系数c与包覆率b的拟合曲线

经对比可以看出，通过基准变形抗力修正后得到的模型比通过回归得到的模型更贴近仿真数据（见图4、图5），仅在500℃情况下稍有偏离。从两种应变速率的对比分析中可知，应变速率对变形抗力模型修正的影响较小，可以忽略。

图4 包覆率20%，应变速率0.1 s-1情况下的基准变形抗力修正应力应变曲线

图5 包覆率20%，应变速率5 s-1情况下的基准变形抗力修正应力应变曲线

将应变速率5 s－1时不同包覆率基准变形抗力修正模型与仿真数据的比较后（见图6～图10） 可以看出，基准变形抗力修正模型能基本上反映不同包覆率时复合材变形抗力的变化情况，仅在450℃、500℃时修正模型比仿真数据偏小，并且这种偏小程度将随着包覆率的增加而加剧。

图6 包覆率13.3%，应变速率1 s-1情况下的基准变形抗力修正应力应变曲线

图7 包覆率20%，应变速率1 s-1情况下的基准变形抗力修正应力应变曲线

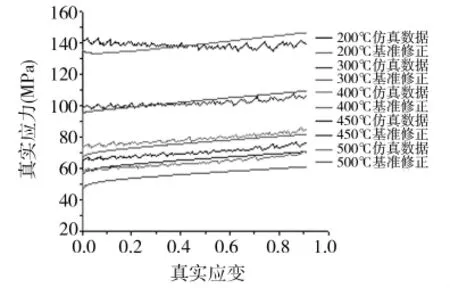
图8 包覆率26.7%，应变速率1 s-1情况下的基准变形抗力修正应力应变曲线

图9 包覆率30%，应变速率1 s-1情况下的基准变形抗力修正应力应变曲线

图10 包覆率33.3%，应变速率1 s-1情况下的基准变形抗力修正应力应变曲线

对不同包覆率，不同温度下基准变形抗力修正模型和仿真数据应力差进行统计后（见表3），可以看出，只要将高温情况下（400～500℃） 的修正模型乘以一个系数就可以实现模型和仿真数据的良好匹配。经过分析得到不同温度下修正模型的系数（见表 4）。

表3 基准变形抗力修正模型和仿真数据应力差 (MPa)

表4 修正模型的系数表

通过对表中的数据进行线性拟合（见图11），可以得到不同温度下的系数a和包覆率b的关系（见式 9）。

图11 系数a与包覆率b的线性拟合图

令 T=t/300，考虑到温度的影响，将式9转化为

则包覆铝合金的变形抗力模型可修正为：

3 结语

(1)在包覆铝合金的热压模拟试验中，因为片层间摩擦力阻碍包覆铝侧向流动将会使变形抗力平稳上升。

(2)热压模拟试验结果揭示出包覆率对合金变形抗力将产生很大影响。

(3)改进模型后得到的预测变形抗力结果和模拟结果高度吻合，说明该模型对于轧制对称包覆铝合金是可用的。

[1]Chi Tianyang,Zheng Lumeifang and Sumitomo．Light Metal Technical Reports,1994，35(1/2):43．

[2]Pen Zhihui(彭志辉)，Luo chunhui(罗春辉)and Gan Weiping(甘 卫 平 ),Journal of central－South Institute of Mining and Metallurgy,1994,25(3):333．

[3]Luo chunhui(罗春辉)，Gan Weiping(甘卫平)and XiaoYaqing(肖亚庆) ．Light Alloy Fabrication Technology．1996:24(4):3．

[4]周纪华．铝合金流动应力数学模型 [J]，北京科技大学学报，1994,16 （4）：351－356．