正则化Bouc-Wen模型的参数研究及其在金属阻尼器中的应用

李宗京， 舒赣平

(1. 东南大学 混凝土及预应力混凝土结构教育部重点实验室, 南京 210096； 2. 东南大学 土木工程学院, 南京 210096)

自从Yao[1]提出结构振动控制的概念以来，结构消能减振技术已经取得了较大的进展和广泛的工程应用[2]。金属阻尼器作为结构被动控制技术中的一个重要分支，由于其构造简单、性能稳定等优势，开始得到越来越多的重视及工程应用[3]。金属阻尼器的滞回力学特性是衡量其耗能减振性能的重要标准。用于描述金属阻尼器的滞回力学行为的常用模型有双(多)线性模型[4-6]、Ramberg-Osgood模型[7-9]、Bouc-Wen模型[9-11]等。双(多)线性模型以直线代替曲线，且存在尖锐拐点，因此模拟精度有限。而Ramberg-Osgood模型和Bouc-Wen均为光滑曲线模型，因此具有较高的模拟精度。此外，Bouc-Wen模型已被SAP2000、MIDAS等多种结构分析商业有限元软件引入[12-13]。因此，Bouc-Wen模型是一种同时具备较高的模拟精度和较好的工程实用性的滞回模型。

本文在经典Bouc-Wen模型的基础上，介绍了一种正则化Bouc-Wen模型，并对正则化Bouc-Wen模型各参数与其所描述的金属阻尼器滞回力学特性之间的关系进行理论推导和分析，研究其各项参数的敏感性区别，最后提出参数拟合方法并进行试验验证。

1 Bouc-Wen模型的正则化

1.1 经典Bouc-Wen模型

Bouc-Wen模型最先由Bouc[14]提出，并由Wen[15]进一步推广，其经典表达式为[16]

F=αku+(1-α)kz

(1a)

(1b)

1.2 正则化Bouc-Wen模型

由式(1)所描述的经典Bouc-Wen模型中存在冗余参数，这导致一条滞回曲线并不对应唯一的一组经典Bouc-Wen模型参数，从而导致无法直接使用经典Bouc-Wen模型进行参数识别。为此，Ikhouane等[17-18]提出了一种正则化Bouc-Wen模型，其表达式为

F=kxu+kww

(2a)

(2b)

式中：F为恢复力；u为位移；w为正则化的内部迟滞变量； 并且w的初值为0，即当t=0时，有w(0)=0。参数kx、kw、ρ、σ、n均会对模型所描述的滞回曲线形状产生相应的影响。其物理模型可简化为如图1所示，即系统的恢复力由线性部分kxu和非线性部分kww并联组成。

图1 正则化Bouc-Wen模型示意图Fig.1 Diagram of normalized Bouc-Wen model

正则化Bouc-Wen模型参数与经典Bouc-Wen模型参数之间的关系为

(3a)

(3b)

kx=αk>0

(3c)

kw=(1-α)kzm>0

(3d)

(3e)

(3f)

式中：zm为经典Bouc-Wen模型中内部迟滞变量z的最大值， 即|z|≤zm， 代入式(3a)可知|w|≤1。 此外，为避免模型发散，需满足n≥1。相比于经典Bouc-Wen模型含有6个参数(k,α,A,β,γ,n)， 正则化Bouc-Wen模型中只含有5个参数(kx,kw,ρ,σ,n)。 根据Ikhouane的研究证明，正则化Bouc-Wen模型与经典Bouc-Wen单元是完全等效的，并且正则化Bouc-Wen模型中不含有冗余参数，从而一条确定的滞回曲线只对应唯一的一组正则化Bouc-Wen模型参数。

2 正则化Bouc-Wen模型参数与金属阻尼器滞回力学特性的关系

图2 金属阻尼器的正则化Bouc-Wen模型及滞回力学特性Fig.2 Normalized Bouc-Wen model and hysteretic characteristics of metallic damper

2.1 初始弹性刚度kd

在t=0处将式(2a)两边对t求导可得

(4)

由于w的初值为0，将w(0)=0代入式(2b)可得

(5)

将式(5)代入式(4)，并考虑到当t=0时，位移u=0，可得

(6)

可见，正则化Bouc-Wen模型所描述的金属阻尼器滞回曲线在原点处的斜率即初始弹性刚度为

kd=kx+ρkw

(7)

当u→∞时，将式(2a)两边对u求导可得

(8)

由于正则化内部迟滞变量w的刚度随位移u的增大而无限趋近于0[17]，即

(9)

将式(9)代入式(8)可得

(10)

可见，正则化Bouc-Wen模型所对应的金属阻尼器的屈服后刚度为

(11)

2.3 屈服位移udy

由于正则化Bouc-Wen模型的恢复力是由线性部分kxu和非线性滞变部分kww所叠加构成，因此其所对应的金属阻尼器屈服位移实际是由正则化内部迟滞变量w所决定的。内部迟滞变量w随位移u在第一象限内的变化关系，如图3所示。

图3 w随u的变化关系Fig.3 Relation between w and u

根据式(5)并考虑到当t=0时，位移u=0，可以得到正则化内部迟滞变量w在原点处的斜率为

(12)

因此w在原点处的切线方程为

w=ρu

(13)

由于正则化内部迟滞变量w随位移u的增大而无限趋近于1[17]， 可知w的渐近线为

w=1

(14)

综上所述，正则化Bouc-Wen模型的屈服位移uy也即其所描述的金属阻尼器的屈服位移udy为w在原点处的切线与w的渐近线的交点所对应的位移，可得

(15)

2.4 屈服力Fdy

由于屈服力Fdy、 屈服位移udy、 初始弹性刚度kd之间满足关系

Fdy=kd·udy

(16)

将式(7)、(15)代入式(16)可得正则化Bouc-Wen模型所描述的金属阻尼器的屈服力为

Fdy=kx/ρ+kw

(17)

2.5 转向刚度ks

(18)

整理后可得发生转向后正则化内部迟滞变量w的斜率为

(19)

将式(2a)两边对u求导可得

(20)

将式(19)代入式(20)可得金属阻尼器滞回曲线在发生转向后的斜率即转向刚度ks为

(21)

另外，根据式(7)，正则化Bouc-Wen模型在原点处的斜率即金属阻尼器的初始弹性刚度为kd=kx+ρkw， 对比式(7)与式(21)可见， 当σ>0.5时，ks>kd； 当0≤σ<0.5时，ks0.5时，滞回曲线在发生转向后的斜率大于滞回曲线在原点处的斜率；当0≤σ<0.5时，滞回曲线在发生转向后的斜率小于滞回曲线在原点处的斜率；当且仅当σ=0.5时，滞回曲线在发生转向后的斜率等于滞回曲线在原点处的斜率。由以上分析可见，转向刚度ks与初始弹性刚度kd之间的相对关系是由参数σ决定的。

图4 参数σ对滞回曲线形状的影响Fig.4 Influence of σ on the shape of the hysteresis curves

2.6 弹塑性过渡段

弹塑性过渡段是Bouc-Wen模型区别于双线性模型的一个重要特点。金属阻尼器采用不同的材料、构造等，均有可能导致其滞回曲线弹塑性过渡段的长短及圆滑程度不同，因此弹塑性过渡段也是体现金属阻尼器滞回特性的一项指标。

(22)

由于|w|≤1， 因此斜率的衰减过程实质上等效于函数y=1-xn， 0≤x≤1的函数值变化过程。 若n较小，则w的斜率较早即开始发生衰减，且衰减的过程较为均匀，相应的过渡段较长、较圆滑；若n较大，则w的斜率只有在当w接近1时才开始发生较为明显的衰减，且迅速衰减至0，相应的过渡段较短、较尖锐。通过Matlab绘制参数n在不同取值下的正则化Bouc-Wen模型滞回曲线如图5所示。当n趋向于无穷大时，过渡段变为一个尖锐拐点，正则化Bouc-Wen模型转变为双线性模型。由以上分析可知，滞回曲线弹塑性过渡段的圆滑度是由参数n决定的。

图5 参数n对滞回曲线形状的影响Fig.5 Influence of n on the shape of the hysteresis curves

3 参数敏感性分析

为进一步评估正则化Bouc-Wen模型各参数对滞回曲线的影响，对其进行参数敏感性分析。参数敏感性分析方法可以分为局部敏感性分析和全局敏感性分析等多种方法[19]，其中局部敏感性分析是一种最直接且易于实施的方法。其分析过程为：先为参数组指定一组基准值，采用控制变量法，当研究某一个参数的敏感性时，只将该参数在其基准值上下变化取值，其他参数均取为基准值保持不变，并比较该参数在不同取值时敏感性评价指标的变化情况。

在本文的参数敏感性分析中，采用局部敏感性分析方法，取参数组基准值为(kx,kw,ρ,σ,n)=(1 kN/mm, 100 kN, 1 mm-1, 0.5, 2)，各参数取值在其基准值基础上分别变化±10%、±20%、±30%、±40%、±50%，并取如下两种敏感性评价指标：

(1) 评价指标1

(23)

(2) 评价指标2

(24)

式中：E为参数组取值改变前一个完整滞回环所包络的面积；E′为参数组取值改变后一个完整滞回环所包络的面积； ΔE为E′与E之间差值的绝对值。η为参数组取值改变前后一个完整滞回环所包络面积的变化量与参数组取值改变前滞回环面积的比值，其代表的是各参数对滞回曲线耗能指标的影响。

基于上述方法，并取加载位移幅值为10倍屈服位移，即[-10 mm , +10 mm]，采样点总数N=200，得到的参数敏感性分析曲线如图6所示。可见采用两种敏感性评价指标均可得到基本一致的分析结果，正则化Bouc-Wen模型对参数kw和ρ较为敏感， 对参数σ、kx和n较不敏感， 并且对参数kw和ρ的敏感度明显高于参数σ、kx和n。

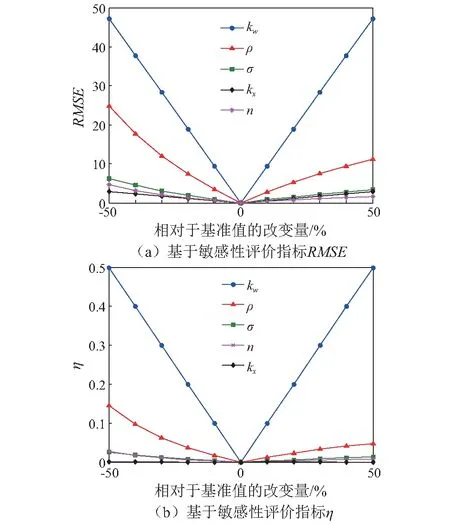
图6 参数敏感性曲线Fig.6 Spider diagram of parameter sensitivity

在对加载幅值进行适当增减后，可以发现加载幅值的增减对其他各项参数的敏感性影响较小，而对参数kx的敏感性影响相对更大。当分别取加载位移幅值为±5 mm、±10 mm、±15 mm时，参数kx基于RMSE评价指标的敏感性曲线如图7所示， 可见kx的敏感性随着加载幅值的增加而增大。其原因是加载幅值增大后，塑性段长度增加，因此塑性段所占比重增大，控制塑性段刚度的参数kx的敏感性随之增强。 此外，当加载幅值在合理范围内变化时，参数kw的敏感性仍然明显小于kw和ρ。 综上所述，kw和ρ为敏感性较高的两个参数，σ、kx和n为敏感性较低的三个参数，各项参数的敏感性排序如表1所示。

图7 加载幅值对参数kx敏感性的影响Fig.7 Influence of loading amplitude on parameter sensitivity of kx

表1 参数敏感性排序表

4 参数拟合方法及试验验证

4.1 拟合方法

设试验得到的金属阻尼器滞回曲线数据点横坐标为ui，纵坐标为Fexp,i，i=1～N， 其中N为数据点总数，由式(2)可以得到相应横坐标处的恢复力拟合值Fsim,i。采用正则化Bouc-Wen模型对试验得到的金属阻尼器滞回曲线拟合，实际可以看作一个优化变量为参数组(kx,kw,ρ,σ,n)，目标函数为均方根误差(RMSE)并使其最小化的非线性优化问题，其中均方根误差为

(25)

本文采用模拟退火算法(Simulated Annealing Algorithm)对上述非线性优化问题进行求解。模拟退火算法最早的思想由Metropolis等[20]提出，并由Kirkpatrick等[21]进一步拓展。其原理是模拟物理退火过程，并采用Metropolis接受准则以一定概率接受较差解，从而使其具有全局搜索能力，有效地避免陷入局部极小点。此外，模拟退火算法不需要梯度等其他辅助信息，且对目标函数无额外要求，具有较强的鲁棒性、全局收敛性、隐含并行性和广泛的适应性，因此已被应用于解决各领域的优化问题[22]。

为了进一步提高算法的效率和结果的质量，本文对传统的模拟退火算法进行了如下改进：

(1) 在算法中设置记忆器，使其成为有记忆功能的模拟退火算法。具体方法为设置一个变量xbest专门用于储存历史最优解，并在每一次迭代中比较当前解xj的目标函数值Ej与xbest的目标函数值Ebest。若当前解xj的目标函数值Ej小于历史最优解xbest的目标函数值Ebest，则采用xj替代xbest，Ej替代Ebest，否则xbest、Ebest保持不变。该措施可以避免在整个搜索过程中错过曾经达到过的最优解，提高算法所得解的质量。

(2) 由于算法收敛到较好结果所需达到的最低温度Tmin事先无法准确预知，故不再以温度达到指定的最低温度作为算法终止准则，改为采用收敛精度作为终止准则，即经过连续若干次迭代，最优目标函数值的改善幅度小于指定的收敛精度ε，则算法终止。

(3) 当搜索空间较大时，由于模拟退火算法等启发式随机搜索优化算法实际上并不能100%保证找到全局最优解，而只能以较大概率接近全局最优解，因此，为了验证算法的稳定性，并增大找到全局最优解的概率，将算法连续运行三次，取三次优化计算结果的最优解作为最终参数拟合结果。

如图8所示为本文采用的改进模拟退火算法流程图，将其中的优化变量x设为正则化Bouc-Wen模型参数组(kx,kw,ρ,σ,n)，并将目标函数E设为均方根误差RMSE， 在Matlab中编程实现迭代算法用于拟合正则化Bouc-Wen模型的参数，并可最终基于拟合结果，根据第2节中的公式得到金属阻尼器的各项滞回力学特性指标。

图8 改进的模拟退火算法流程图Fig.8 Flowchart of improved simulated annealing algorithm

4.2 试验验证

TADAS装置是一种典型的金属阻尼器[23-25]，其原理是通过三角形耗能钢板的弯曲塑性变形实现耗能。为研究TADAS装置的滞回性能、评定其滞回力学特性指标，并验证正则化Bouc-Wen模型对其滞回曲线的拟合效果，本文在东南大学结构试验室对该装置进行了拟静力往复加载试验研究。试验中采用的TADAS装置由四片相同的三角形耗能板及连接顶板、连接底板和两块插槽板构成，如图9所示。三角形耗能板使用Q345材质12 mm厚的钢板制做。试验装置如图10所示，将TADAS装置试验件安装于铰接框架中进行往复加载。TADAS装置在加载过程中的变形形态如图11所示。

图9 TADAS装置试验试件示意图Fig.9 Diagram of the TADAS device for the test

图10 试验装置Fig.10 Test setup

图11 TADAS装置变形形态Fig.11 Deformed shape of TADAS device

通过往复加载试验得到的滞回曲线及采用本文提出的基于改进模拟退火算法的拟合曲线如图12所示，可见拟合曲线与试验曲线能够较好吻合。三次拟合过程的迭代曲线如图13所示，由于采用了历史最优解记忆器，并将迭代曲线的纵坐标轴取为历史最优解的目标函数值Ebest，因此迭代曲线成单调递减的阶梯状。相应的参数拟合结果如表2所示。三次拟合结果的目标函数值基本相同，目标函数值的最大相对偏差在5%以内；敏感性较高的参数的拟合结果也基本一致，最大相对偏差均在5%以内；但敏感性较低的参数的拟合结果存在一定偏差，尤其是参数σ和n的最大相对偏差分别达到10%和30%以上。其主要原因是敏感性较低的参数对目标函数RMSE的影响相对较小，因此其在一定范围内变化时不会对目标函数RMSE造成明显影响。此外，对于敏感性较低的参数n，由于实际中金属阻尼器一般不会出现过于尖锐的拐点，且当参数n的取值差别较小时，弹塑性过渡段的变化并不明显，故建议可将其取值范围限定在1～10之间的整数，从而进一步提高参数拟合效率。正则化Bouc-Wen模型参数拟合完成后，可以进一步根据第2节中的公式得到金属阻尼器的各项滞回力学特性指标，此处不再赘述。

图12 试验滞回曲线及拟合滞回曲线Fig.12 Hysteresis curves by test and simulation

图13 拟合过程迭代曲线Fig.13 Iteration curves of identification process

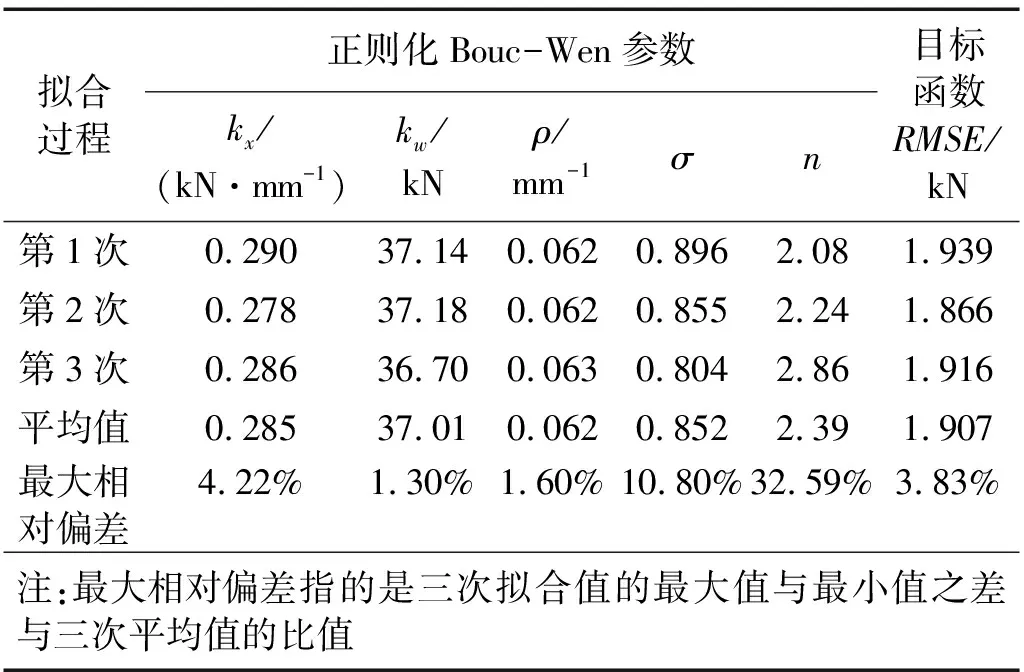
表2 参数拟合结果

5 结 论

本文对正则化Bouc-Wen模型中的各项参数进行了相关理论推导及敏感性分析，提出了相应的参数拟合方法并进行了试验验证。主要研究成果如下：

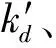
(2) 基于两种不同的敏感性评价指标，均可得到正则化Bouc-Wen模型敏感性较高的两个参数为kw、ρ，敏感性较低的三个参数为kx、σ、n。

(3) 改进的模拟退火算法能够有效实现对正则化Bouc-Wen模型的参数拟合，并且拟合滞回曲线与试验滞回曲线能够较好吻合。

本文的相关研究成果能够为正则化Bouc-Wen模型在金属阻尼器中的应用提供有效依据，并提供了金属阻尼器滞回曲线拟合及滞回力学特性指标评定的一种有效方法，对于金属阻尼器的设计、应用及性能评估具有重要参考意义。