题根（计数原理）

倪伟

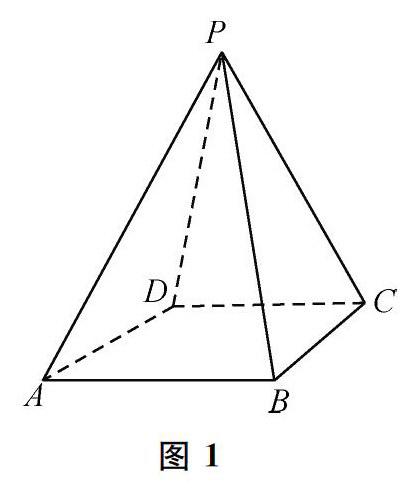
题 （1）如图1，将一个四棱锥P-ABCD的每个顶点染上一种颜色，并使同一条棱的两端异色，若只有5种颜色可供使用，求不同的染色方法总数.

（2）甲、乙、丙3人互相传1只篮球，开始球在甲手中，经过5次传球后，球还在甲手中，求不同的传球方法总数.

一、寻根

这两道题目的共同点在于都是计数问题，计数问题最根本的解决方法是一一数之（枚举法）和综合利用计数原理（分类与分步计数原理）.对于题（2），方法种数不多，可以使用枚举法，但是为了更好地解决一类问题，我们常常需要建立一些数学模型.

如若题（1）中去掉“四棱锥”的这一包装，题即变为：用5种颜色给P，A，B，C，D5个点染色，每个点染一种颜色，相邻两点不同色.五点中，除A与C、B与D不相邻，其余都相邻，求不同的染法种数.在解决该问题时，我们可以联想计数问题中的一道经典染色问题（见题根）.

题（2）是一个传球问题，和题（1）能否联系起来呢？亦即是要找到题中的“点”和“颜色”，若我们将甲、乙、丙看作“点”，传球方式看成在染色，发现难以转化，因为无法理解相邻异色.而本题中隐藏条件“自己不能传给自己”疑似和“相邻两点不同色”相关，因此我们可以试着将传给谁看成染什么色，把5次传球看作5个“点”，问题即转化为：用红、黄、蓝三种颜色给P，A，B，C，D5个点染色，每个点染一种颜色，相邻两点不同色，其中点D只能染红色，P，A，B，C，D围成一圈，依次相邻，如图2所示，因此我们可以发现这两道题都可以看成同一类问题——染色问题.

二、题根

题根：如图3，用5种不同的颜色给图中4个区域染色，每个区域染一种颜色，要使相邻区域不同色，求不同的染色方法种数.

分析一：首先我们要搞清本题需要完成的一件事——将4块区域染好颜色.

这件事我们分四步完成：

第一步：我们染1号区域，共有5种方法；

第二步：染2号区域，只能从余下的颜色中选一种，共有4种方法；

第三步：染3号区域，由于其和2号相邻，因此也有4种方法；

第四步：染4号区域，4号和1号与3号均相邻，而3号与1号可能同色，也可能异色，因此我们需要重新对3号区域的染色分析.完成这件事我们将其分为两类：第一类是当3号与1号同色，则染3号区域只有1种方法，此时染4号区域，共有4种方法；第二类是当3号与1号异色，则染3号有3种方法，此时染4号区域，共有3种方法.

因此共计有5×4×（1×4+3×3）=260种方法.

分析二：上述方法，是按区域进行分步染色，我们也可以理解为这样完成一件事——先选好颜色，再染色.通过观察，1号区域和3号区域、2号区域和4号区域不相邻，这两组区域可以同色，也可以异色，因此4块区域用到2、3或4种不同的颜色.

完成这件事我们可以分三类：

于是我们可以将该问题一般化：

用m种不同的颜色给图4中n个区域染色，每个区域染一种颜色，要使相邻区域不同色，求不同的染色方法种数.

我们试着按区域进行分步染色，1号区域有m种方法，2号区域有（m-1）种方法，3号区域有（m-1）种方法……（n-1）号区域有（m-1）种方法，最后染n号区域时，需要考虑1号和（n-1）号是否同色，而它们是否同色，还需思考1号和（n-2）号是否同色……如果直接去分类，就很困难了.但我们换个角度，暂不考虑n号区域受1号区域影响，直接染n号区域时，出现两类：一类是1号区域和n号区域异色，这是我们需要的情况；另一类是1号区域和n号区域同色，这是我们不需要的，而这种情况中，我们将1号区域和n号区域看成整体，就相当于用m种不同的颜色给（n-1）个区域染色，即用递推关系去解决问题.

通过将问题一般化，我们就得到了一个涂色问题的模型，亦即该类问题的“题根”.三、解答（1）第一步，先将P点染色，共有5种方法；第二步，再染其他4个点，相当于题根故本题共有5×84=420种方法.

（2）方法一：枚舉法（画出树状图，如图5所示）.其右10种.

计数问题中有很多经典的模型，可以看作“题根”，在解决一些新的问题时，我们试着将问题转化为与题根相关的问题，会达到事半功倍的效果.