从四个命题角度例谈“牛顿运动定律的综合应用”

肖建华

牛顿运动定律是动力学的基本规律，力学的核心知识，像一条引线贯穿高中物理的始终.对牛顿运动定律的综合应用，常以实际问题为背景来命题，考查学生获取并处理信息的能力，数形结合解决问题的能力，把实际问题转化成物理模型的能力，综合运用运动学公式和牛顿第二定律的能力.

“牛顿运动定律的综合应用”主要的命题视角有：超重失重问题、动力学中的图象问题、临界状态和极值问题、传送带问题、连接体问题、板块模型问题等.这几类问题往往以真实物理现象为依据的问题，它既能很好地培养学生的学科素养，又能联系科学、生产和生活实际，具有生命力，是高考的热点，近几年各地高考中都出现过，2014年江苏高考压轴题就是传送带问题.本文从其中三个命题视角展开讨论.

命题视角一：超重与失重问题

例1 如图1所示是某同学站在力传感器上做下蹲一起立的动作时记录的压力F随时间t变化的图线.由图线可知该同学

（）

A.体重约为650 N

B.做了两次下蹲一起立的动作

C.做了一次下蹲一起立的动作，且下蹲后约2s起立

D.下蹲过程中先处于超重状态后处于失重状态

解析 从图中可以看出人的体重约为650 N，A正确；人下蹲动作分别有失重和超重两个过程，先是加速下降失重，到达一个最大速度后再减速下降超重，对应先失重再超重，起立对应先超重再失重，对应图象可知，该同学做了一次下蹲一起立的动作，B错误；由图象看出两次超重的时间间隔就是人蹲在地上持续的时间，约2s，C正确；下蹲过程先失重后超重，D错误.

故选：AC.

【方法提炼】两个关键点：（1）理解图象的物理含义，如坐标轴、正负等的含义；（2）判断超重失重的两个角度：受力角度和加速度角度.一般思路：压力（或拉力）和重力的比较（超重或失重）加速度的方向（超重或失重）运动情况.

命题视角二：动力学中的图象问题

例2 如图2（a），一物块在t=0时刻滑上一固定斜面，其运动的v-t图线如图2（b）所示.若重力加速度及图中的v0、v1、t1.均为已知量，则可求出 （）

A.斜面的倾角

B.物块的质量

C.物块与斜面间的动摩擦因数

D.物块沿斜面向上滑行的最大高度

解析 由图（b）可知，物体先向上减速到达最高时再向下加速；图象与时间轴围成的面积为物体经过的位移，故可出物体在斜面上的位移；图象的斜率表示加速度，上升过程及下降过程加速度均可求，上升过程有：

mgsinθ+μmgcosθ=ma1

下降过程有：

mgsinθ-μmgcos θ=ma2

两式联立可求得斜面倾角及动摩擦因数；但由于m均消去，故无法求得质量；因已知上升位移及夹角，则可求得上升的最大高度.

故选：ACD.

【方法提炼】弄清运动情况，正确受力分析，列出牛顿第二定律的方程，整理出与对应图象相关的函数表达式；着重理解纵横坐标轴截距的含义，分析图线的斜率、面积、截距等表示的物理意义.解题策略：

命题视角三：传送带问题

例3 如图3甲所示，绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小物块滑上传送带开始计时，小物块在传送带上运动的v-t图象（以地面为参考系）如图乙所示.已知v2 >vl，则

（）

A.t2时刻，小物块离A处的距离达到最大

B.t2时刻，小物块相对传送带滑动的距离达到最大

C.0～t2时间内，小物块受到的摩擦力方向先向右后向左

D.0～t2时间内，小物块始终受到大小不变的摩擦力作用

解析 速度一时间图象与时间轴围成的面积代表位移，时间轴上面的部分表示位移为正，下面的部分表示位移为负，据此判断t1时刻位移最大，选项A错.0 -t1时间段，小物块速度与传送带速度方向相反，相对传送带向左运动，摩擦力方向向有，t1- t2时间段，虽然小物块与传送带速度同向，但小物块速度小于传送带速度，相对传送带仍然是向左运动，摩擦力方向向右，t2时刻后，由于v2>v1，所以与传送带速度相同保持相对静止，对照选项BD对，C错.

答案 BD

例4 如图4所示，足够长的粗糙的传送带与水平面夹角为θ，以速度v0逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块，则下图中小木块的速度随时间变化关系中可能正确的是

（）

解析 初始阶段物块比传送带慢，相对传送带向上运动，滑动摩擦力沿斜面向下，分析斜面方向受力有

mgsin θ+μmgcos θ=ma1

a1=gsin θ+μgcosθ

即第一阶段为匀加速直线运动，排除答案A，当物体匀加速到等于传送带速度后，若沿斜面向下的重力分力mgsinθ小于等于最大静摩擦力μmgcos θ，则物块和传送带相对静止一起匀速运动；若沿斜面向下的重力分力mgsinη大于最大静摩擦力μmgcosθ，物块继续向下加速，不过摩擦力变为沿斜面向上，此时a2=gsin θ-μgcosθ，此时继续向下匀加速，但是加速度比第一阶段要小，所以，答案为CD.

答案 CD

【方法提炼】抓住关键点：受力分析（尤其是摩擦力的分析）、过程分析、关键状态（共速或速度为零）分析.主要流程：

命题视角四：板块问题

例5 一长木板置于粗糙水平地面上，木板左端放置一小物块；在木板右方有一墙壁，木板右端与墙壁的距离为4.5 m，如图6（a）所示.t=0时刻开始，小物块与木板一起以共同速度向右运动，直至t=ls时木板与墙壁碰撞（碰撞时间极短）.碰撞前后木板速度大小不变，方向相反：运动过程中小物块始终未离开木板.已知碰撞后1 s时间内小物块的v-t图线如图6（b）所示.木板的质量是小物块质量的15倍，重力加速度大小g取10 m/s2.求：

（1）木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2；

（2）木板的最小长度；

（3）木板右端离墙壁的最终距离.

解析 （1）规定向有为速度的正方向.木板与墙壁相碰前，小物块和木板一起向右做匀变速运动，设加速度為a1，小物块和木板的质量分别为m和M.由牛顿第二定律有

-μ1（m+M）g=（m+M）a1

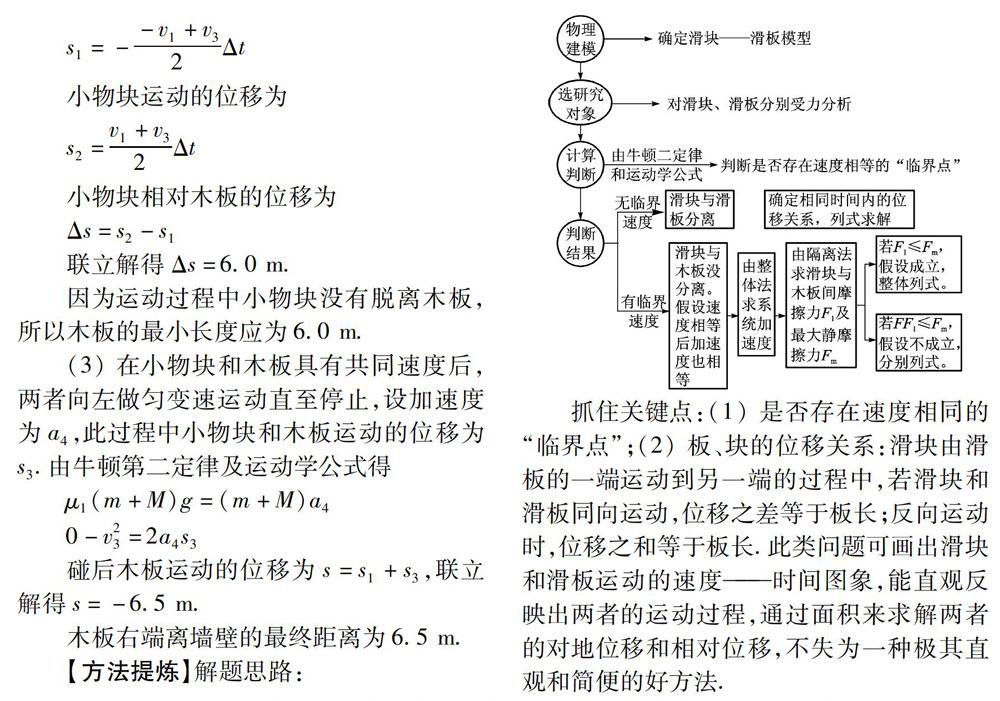
抓住关键点：（1）是否存在速度相同的“临界点”；（2）板、块的位移关系：滑块由滑板的一端运动到另一端的过程中，若滑块和滑板同向运动，位移之差等于板长；反向运动时，位移之和等于板长.此类问题可画出滑块和滑板运动的速度——时间图象，能直观反映出两者的运动过程，通过面积来求解两者的对地位移和相对位移，不失为一种极其直观和简便的好方法.