数学活动，把学生的思维引向深处

江苏睢宁县实验小学（221200）

古人云：“纸上得来终觉浅，绝知此事要躬行。”可见，有意义的数学活动对学生的数学学习是多么重要。因此，教师要给学生创设动手实践活动的机会和时间，让学生在活动中思考、质疑、探究，以形成良好的学习能力和学习习惯。

一、基于教材，创设有效的数学活动

“教材”是教师从事教学活动的最重要依据。新苏教版教材设置了较多的动手实践活动，作为教师必须要领悟教材的编写意图，引领学生通过有效的数学活动学习新知。现以新苏教版教材五年级下册“倍数和因数”的教学内容为例，对教材设置的数学活动进行分析。

新教材的内容与旧教材有很大不同。旧教材是先建立整除的概念，再在此基础上介绍因数和倍数。新教材是直接介绍因数和倍数，在揭示因数和倍数的概念之前设置“用12个大小相等的小正方形摆长方形，有几种摆法”的情境。教材这样改变的用意是什么？笔者带着诸多疑问和困惑再次研读教材，渐渐明白了教材设计和安排的“良苦用心”。

1.通过“摆”的活动，让学生构建具体直观的数学模型

“用12个大小相等的小正方形摆长方形，可以怎么摆，有几种摆法？”这个问题对于五年级的学生来讲很简单，况且他们在上册刚刚学习过“一一列举”的策略，解决这类问题已经有了一定的基础和经验，所以教师可放手让他们“摆”。当然，这里的“摆”并不一定真的动手去摆，可以通过不同的形式呈现“摆”的过程，如画图、列表、列乘法算式等，但是不管用哪种方式，学生的头脑中都会快速呈现自己所“摆”的图，他们所给出的表格或算式也都是来源于头脑中所“摆”的图，且他们在思考的时候基本都能够做到有序不重复。如：

在摆的过程中，学生随着“有序思考”还会给出2×6=12，3×4=12等重复算式，但是稍作思考和观察，学生便不难发现这种重复的现象。

通过这种直观的操作，学生不仅能够明白1、2、3、4、6、12为什么是12的因数，同时也能明白5、7、8、9等数为什么不是12的因数。当学生的头脑中有了“因数和倍数”的数学模型，就能为如何去找一个数的因数和倍数在方法上提供铺垫和支撑。

2.以直观模型为基础，揭示抽象数学概念

以具体的直观图形为例，如：

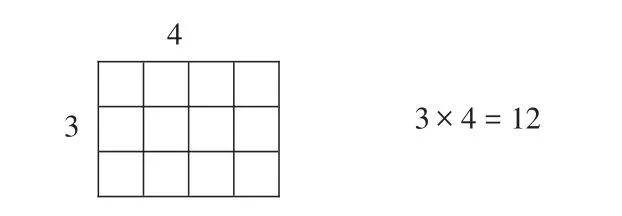
教师可以指出：如果用12个大小一样的小正方形摆长方形，每排摆4个，正好摆3排，就可以说3是12的因数，4也是12的因数；12是3的倍数，12也是4的倍数。教师利用直观图揭示因数和倍数的概念，使概念的揭示具体化和直观化，突破从抽象到抽象，从数字到数字的固有模式，让学生自主体验数与形的结合，降低了理解概念的难度，从而让学生真正理解和接受因数和倍数这对概念的原理和内涵。

3.以直观模型为媒介，把学生的思维引向深处

当学生的头脑中已经建立了具体的直观图，明白因数和倍数概念产生的数学模型后，学生自然会知道如何去找一个数的因数。这时，教师可把例1和例2有机地结合在一起。

有了数学模型的支撑，对于“1为什么是一个数最小的因数？一个数最大的因数为什么是它本身？0为什么不是一个数的因数？任何数都会有因数吗？最少会是几个？”……学生利用头脑中的数学模型都能淋漓尽致地进行解释，而不需要通过观察抽象的数字总结发现，学生不仅知道了是什么，而且明白了为什么。

显然，越是抽象的数学概念越要通过直观模型来建立，从而凸显数形结合的重要意义。

二、活用教材，创设有效的数学活动

苏教版教材四年级上册“画角”的内容是一节操作技能课，对于四年级的学生来说有一定的难度，教师不能把技能的形成仅仅落在反复说教和重复练习上。任何技能的形成都是有基本原理和内涵的，只有充分把握了原理和内涵，在具体的操作上才不容易出错，才有利于基本技能的形成。

1.用三角板“印”角的活动

师：你知道三角板上的每个角的度数吗？

师（拿出一个有30度角的三角板，指着30度的角）：现在我们可以画出一个30度的角吗？

（学生尝试操作）

师：你画出来的角为什么就是30度？（明确：把三角板上的30度角“印”到纸上来，纸上的角和三角板上的角是重合的，所以是30度）

一个简单的数学活动，关注到了画角的数学内涵和基本原理，这个“印”字非常形象地说明了画角的“重合”原理，同时也把画角的动作技能体现出来了，为学生学习新知做好了铺垫。

2.用量角器“印”角的活动

设计画一个50度角的活动。活动要求：

（1）独立思考怎样画；

（2）思考后试着画一画；

（3）尝试把画的过程中遇到的困难或疑惑简单地记录下来；

（4）在小组里说一说自己的想法、做法和自己遇到的困难。

一个简单而开放的数学活动，给学生提供了足够的思考和探究空间，培养了学生深入思考与探究的习惯。

学生知道要想画角需要先找到相应度数的角，然后想办法把它“印”下来。显然，“印角”时用量角器要比三角板这种模具难操作，学生尝试的时候会遇到很多困难，但这恰恰是学生必须去经历的，只有遇到了困难，并且想办法解决了困难的这个过程，获得的东西才真正是自己的东西，才是终身能够受用的东西。

课后，一张张看似平常的作业纸上呈现了学生思维的轨迹：“明明看到了角的顶点，可是我却没办法把它描下来。”“量角器的中心半圆为什么不制作成空心的？那样我就可以画出角的顶点了。”“用量角器画角怎么这么难，明明50度角就在眼前，我却画不下来。”……这些都是学生真实的心声。有一个学生还写道：“我一开始总是画不好，直到第11次才把50度角准确地画出来。”不厌其烦的思考，不言放弃的实践，这些对于学生来说是多么宝贵的收获和经历啊！可以看到，画角的技能完全放手给学生去探究的确存在着较大的难度，几乎每个学生都经历了从一开始的“束手无策”到思考后的“稍有眉目”，再到尝试后的“逐渐明晰”的一个过程。学生作业纸上所画的50度角上有很多擦痕，这正是他们思考、实践和调整的印迹，这也许就是“最美的收获”。

人们需要通过“触感”来激发求知欲，所谓知识的“触感”，从数学学科来说，便是通过有效的数学活动，在活动中领悟知识的存在与价值。如果能让学生在真实的活动中感知到知识的存在，以及知识对解决实际问题的效果，学生的求知行为就会形成良性循环。