数学史融入数学课堂的个案研究

江苏南通市唐闸小学（226000） 刘 莉

【课题】神奇的数

【教学内容】苏教版教材五年级下册因数和倍数单元“你知道吗？”

【教学目标】

1.探索完美数和斐波那契数列的相关知识；

2.通过探索，感受猜想和探究的重要性；

3.学会探究数学规律的一般方法，激发学生对数学学习的兴趣。

【教学重难点】探索完美数和斐波那契数列。

【教学过程】

一、课前欣赏

师（出示“神奇的大自然”微视频）：大自然神奇吗？其实数学和大自然一样神奇。今天，就让我们带着智慧的眼、好奇的心，一起探索神奇的数。

【设计意图：通过感受大自然的美，感受数学与大自然息息相关。】

二、认识完美数

师：在上个单元的学习中，我们认识了因数，说说这几个数的因数有哪些？其实因数中还藏着一些秘密，想知道吗？

师：这里每个数的因数中，除本身外，算一算其余的因数的和，再与本身比一比，哪个数与众不同？

生1∶6。

师：它有什么特别之处？

生2：6的因数有1、2、3、6，除6以外的因数是1、2、3，相加的和正好是6本身。

师：像6这样的数，叫作完全数。完全数是数学中最美妙的一类数，也叫完美数。回味一下，什么样的数，能称为完美数？

【设计意图：从完美数的特别之处揭示完美数的概念，激发学生探索完美数的兴趣。】

师：你们想寻找下一个完美数吗？准备怎样找？

（引导学生有序思考，组织学生分组探究）

生3：28的因数有1、2、4、7、14、28，1+2+4+7+14=28。

师：太好了，终于找到了！

【设计意图：寻找完美数的设置，目的在于让学生经历探究的全过程，虽然有些漫长，也不断经历失败，但是在失败中学生学会了合作，学会了坚持，积累了学习经验，最终体会到发现的快乐。】

师：我们通过耐心地列举，细心地计算，小心地验证，终于找到第二个完美数——28，我们的发现和数学家的发现完全一样。看来，要成为数学家也不是那么遥不可及的事情。

【设计意图：让学生感悟到数学家探索的过程也是这样的漫长，也是困难重重，只有坚持不懈、勇于挑战，才能发现更多数学奥秘。】

三、认识并进一步探索斐波那契数列

师（播放微视频）：这个数列叫什么？（斐波那契数列）斐波那契数列究竟有什么神奇之处呢？

生1：1+1=2，1+2=3，2+3=5……

师：以此类推，有什么规律？

生2：前2个数之和等于后一个数。

师：斐波那契数列在自然界中经常出现，最能给人启发的是这些数呈现出的漂亮模式。

（教师引导学生看到隐藏的斐波那契数列，要求学生拿出探究单，小组合作一起研究）

生3：6=2×3，15=3×5，40=5×8……

师：为什么1、1、2、3、5和8的平方数之和等于8×13？

师：数学家华罗庚爷爷说过“数形结合百般好！”，那么老师就用一个简单的图形来解释。

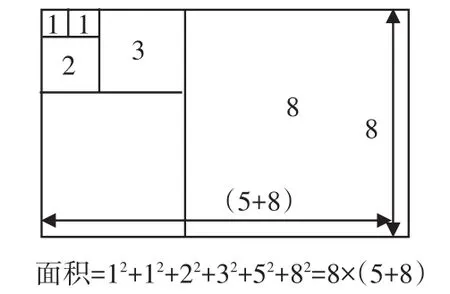
这个长方形的面积是多少？

一方面：面积=组成它的小正方形的面积之和，

它的面积=12+12+22+32+52+82=104；

另一方面：这是一个长方形，面积=长×宽，宽是8，长是（8+5），面积就等于8×（5+8）=104；

不同的方法，但都是同一个长方形的面积，计算出来的结果一定是相等的。

那么1，1，2，3，5，8的平方和一定等于8×13。

师：很多数学知识都有着妙不可言的一面。我们研究完美数和斐波那契数列，都是希望同学们能学会观察，学会思考！

【案例反思】

一、数学史融入课堂不是为了数学史的教学，而是为了数学教学

在本节课中，执教者结合因数单元的知识，对苏教版教材五年级下册“你知道吗？”中的简单内容“完全数知识”进行了合理补充和适当拓展，精心地进行教材重组，设计了适合学生研究的教学环节，引导学生沿着科学家探索发现的路径走一走，不仅巩固了因数的知识，更让学生经历了探究中会经历的失败、无奈，但最终又在坚持中获得了成功的全过程，体验了发现后的快乐和成就感，这样的过程是有价值的。

其次，在探索斐波那契数列的过程中，不仅仅是为认识数列本身的规律，由此衍生出的其他规律，更能激发学生的学习兴趣，尤其是数形结合帮助学生理解“为什么12+12+22+32+52+82=8×（5+8）”，更是课堂中的一个亮点。这种课堂，是能激发学生深度思考的课堂，更是能提升学生数学素养的课堂。

虽然斐波那契数列并非苏教版教材中的内容，但是作为一名数学教师应该了解这个数列，也值得教师带领学生去研究这个数列的内涵。执教者借助“认识完美数”的契机，将斐波那契数列融入课堂，以“神奇的数”为题，巧妙地引入数学史的知识，让学生在短短四十分钟的课堂上收获了更多的数学知识，还渗透了数学思想，这样的课堂怎能不受学生青睐？

二、数学史融入课堂是为了更好地顺应逻辑走向

教师引领着课堂，教师的教学理念和教学思想直接决定了课堂的深度。如果教师能够关注儿童的生活经验，寻找数学知识的来源，那么教学就会符合生活的逻辑，学生的学习就像呼吸一样自然。

如果教师了解数学史，就可以用浅显的情境去凸显数学思想的深刻内涵，使得数学教育于具体中见深邃，于浅显中见厚重，教学就能焕发思想的光芒和经典的力量。

三、数学史融入课堂是为数学本质的呈现提供厚实的背景

课堂教学中的“教”与“学”，都是围绕教学内容展开的。将数学史融入课堂，就是为数学本质的呈现提供了厚实的背景，在强有力的背景支撑下，抽象的数学概念将变得丰富和生动。

综上所述，作为一名数学教师，不但要研读数学史，还要创造性地将数学史融入数学教学，这不仅是有意义的，更是必要的。只有让数学史成为数学课程的组成部分，润物无声般地进入课堂，才能使数学课堂反映出数学背后厚重的历史。