让思维向纵深处伸展——“长方体、正方体的体积计算公式”教学设计与思考

江苏南京市琅琊路小学威尼斯水城分校（210000）

【教学内容】苏教版教材六年级（上册）第16～17页，例9和例10，“试一试”和“练一练”，练习四第1～3题

【教学目标】

1.让学生在操作、观察、猜想、验证、交流和归纳等数学活动的过程，探索并掌握长方体和正方体的体积计算公式，能应用公式正确计算长方体和正方体的体积，并解决相应的简单实际问题。

2.让学生在数学活动中，进一步积累探索数学问题的经验，提升数学思维水平，培养探索精神和实践能力，形成积极的情感态度。

【教学过程】

一、开门见山，提出问题

师：上节课我们认识了体积和体积单位，今天这节课接着来研究长方体和正方体的体积。看到这个课题，你认为长方体和正方体的体积跟什么有关？

师：今天老师带来棱长为1厘米的小正方体，你知道它的体积是多少吗？今天这节课就借用这个1立方厘米的小正方体来研究长方体和正方体的体积。

【评析：问题是思维的起点，是探索的动力。让学生大胆猜测“长方体和正方体的体积跟什么有关”，既调动了学生已有的知识经验，又激发了学生的好奇心，吸引了学生的注意力，教会学生如何提出问题，如何思考。】

二、猜想验证，探究问题

1.探究长方体体积公式

[活动一]

活动要求：用若干个1立方厘米的小正方体摆出不同的长方体，然后把相应的数据填写在表格里。

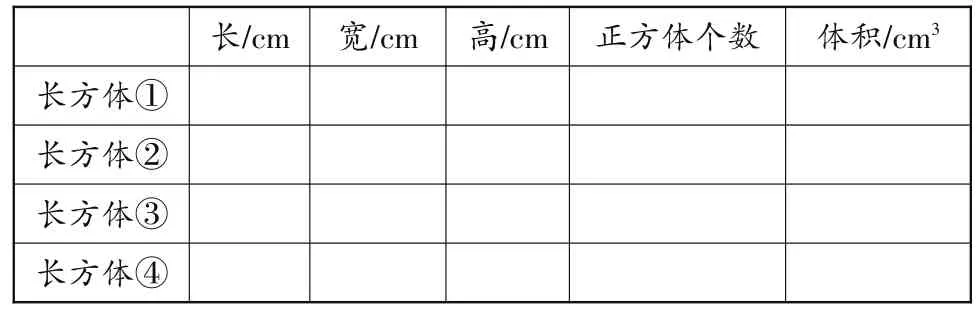
___________长/cm__宽/cm__高/cm__正方体个数 体积/cm3_长方体________________________________________________①_长方体②_长方体③_长方体_________________________________________________④

小组交流：这些长方体的长、宽、高各是多少？用了几个小正方体？怎样很快能知道用的小正方体的个数？长方体的体积是多少？

全班交流:摆出的长方体的体积与小正方体的个数有什么关系？（引导学生明确小正方体的个数就是长方体体积的立方厘米数；长方体的长、宽、高的数量越大，所用的1立方厘米正方体的个数就越多，长方体的体积也就越大）

师：长方体的体积与它的长、宽、高有什么关系？我们刚才只求出4个长方体的体积，所有长方体的体积都等于长×宽×高吗？

师（出示例10的第一个长方体）：这个长方体的体积是4×1×1吗？为什么有的同学不确定了？看来关于长方体的体积还要进一步验证。

[活动二]

活动要求：

（1）用1立方厘米的小正方体摆出下面的长方体（如下图），先想一想各需要多少个小正方体，再摆一摆。

（2）填写表格（略），说说每个长方体各用了几个小正方体，它们的体积分别是多少立方厘米。

全班交流：①长方体的长、宽、高分别是多少？体积分别是多少立方厘米？这个结果与我们刚才的猜想是否一致？②摆出的长方体的长是几？长的数量表示什么（第一层摆几个）？摆出的长方体的宽是几（摆几行）？宽的数量表示什么？长与宽的乘积计算的是什么？摆出的长方体的高是几？高表示什么(摆几层)？长方体的长、宽、高分别是多少？

师：无论是你们摆的长方体，还是老师给出的长方体，你们觉得长方体的体积跟什么有关？“长×宽”算的是什么（一层有几个体积单位）？再乘高呢？（几层一共有多少个体积单位）

（学生自学课本16页长方体体积公式，交流汇报：V=abh）

【评析：当学生利用学具动手操作、猜想、验证、交流，得出无论自己摆出的长方体还是老师给出的长方体的体积计算公式时，教师鼓励学生互动，理清公式的意义：“先求一层有几个，再乘层数，得到小正方体的个数就是长方体的体积数。”这样，让学生带着问题猜想，放手让他们充分探究、验证猜想，在不断的思维碰撞中初步解决问题，发展学生的空间观念。】

2.推导正方体体积公式

师：正方体是特殊的长方体，你能根据长方体的体积公式推导出正方体的体积公式吗？

生1：因为正方体是特殊的长方体，正方体具有长方体所有的特征，是长、宽、高相等的正方体，而长方体的体积=长×宽×高，所以正方体的体积=棱长×棱长×棱长。

生2：如果用刚才测量长方体的小正方体去测量正方体的体积，每行摆的个数、摆的行数、摆的层数都相等，也就是都与正方体的棱长相等，所以正方体的体积=棱长×棱长×棱长。

师：请读一读课本第17页，说说正方体体积的字母公式，明确a3的含义、读写方法。（出示练习教材第17页“练一练”第2题。计算：33；53；13；103；0.13）

3.归纳提升

师：讨论长方体和正方体的体积计算方法是否相同。

【评析：当学生已经得出长方体和正方体的体积公式之后，教师通过让学生比较两个立体图形的公式，把学生的思维引向深处，得出“长方体和正方体体积计算实质是一样的”，为下一节课的学习奠定了基础。】

三、实际应用，发展提升

1.教材第17页“试一试”。

2.教材第17页“练一练”第1题。

3.教材第20页练习四第1～3题。

【教学思考】

“长方体、正方体的体积计算公式”是在学生已经掌握长方体和正方体的特征，了解体积的意义并认识体积单位的基础上学习的内容，也是立体图形体积计算的第一节课。因此，教师在制定教学目标时，不能只定位在让学生记忆并套用公式计算上，而应关注学生对体积意义和体积单位的理解，并在此基础上提升学生的数学思维水平，培养学生的探究精神和实践能力。

郑毓信教授指出：“数学核心素养的基本含义就在于：我们应当通过数学教学帮助学生学会思维，并能使他们逐步学会想得更清晰、更深入、更全面、更合理。”教师不仅要关注学生应该学到什么，还要重视他们是怎样学到的，也就是说，要展现学生数学思维的过程，引导学生逐步学会用数学思维解决问题。

1.动手操作，启迪思维

体积对于学生来说是一个新概念，由平面图形到立体图形，是学生空间观念的一次重大跨越。教师应注意加强学具的演示和学生的动手操作活动，以发展学生的空间观念，加深学生对长方体计算公式的理解。在探索长方体体积公式的过程中，教师安排了两次操作活动，第一次是没有规定长方体的长、宽、高，学生任意摆出不同的长方体，；第二次是规定了长方体的长、宽、高，学生根据教师给的图形摆出长方体。两次操作活动，层次不同，学生获得的体验也不同。第一次的操作，让学生初步体会到长方体的体积与长、宽、高有关，第二次的操作，让学生进一步体会到“摆出的长方体的长的数量与沿着长摆的体积单位个数有关；摆出的长方体的宽的数量就是沿着宽应该摆出的体积单位；摆出的长方体的高的数量就是摆的体积单位的层数”。动手操作，使学生对体积的理解更加清晰、明确，启发了学生的思维，为推导体积公式打下坚实的基础。

2.问题引领，活跃思维

数学课堂的核心是思维，而设置问题是让学生实现有效思维的方法，正确引导学生基于问题有效、高效地思维，能不断提升学生的数学思维能力，从而使学生获得可持续发展的能力。课始，教师在学生已有的知识经验基础上引导学生猜测“你认为长方体的体积跟什么有关？”；在学生有一定操作的基础上又一次引导学生猜测“长方体的体积与它的长、宽、高有什么关系？”；接着又问“是不是所有长方体的体积都是长×宽×高？”。这样有步骤地引导学生多角度、多层次地思考问题，学生的思维在教师一次次精心设计的问题中更加活跃，对长方体和正方体的体积理解得更加深入。

3.反思过程，提升思维

对学习过程进行反思，不仅可以检查和评价自己对所学知识的理解是否正确，而且可以进一步了解所学的数学知识是哪些原有知识的扩充与发展，从而提高理解和掌握知识的水平。如，在两次操作活动后，教师引导学生反思操作过程，以体积与长、宽、高的关系推导并理解长方体的体积计算公式；再如，在学习正方体的体积公式时，教师引导学生思考“正方体是特殊的长方体，你能根据长方体的体积公式推导出正方体的体积公式吗？”学生就能反思长方体公式的推导过程，逐渐构建数学认知。

费赖登塔尔说过：“学习数学的唯一正确的方法是实行再创造，也就是由学生本人把要学的东西自己去发现或创造出来。”学生思维的发展需要建立在已有的知识经验基础之上，教师要激活学生已有的知识经验，激发学生开展数学思维的内在动力，给学生充分展示数学思维的机会，通过对话、提问等方式促进学生思维水平的逐步提升，给予学生努力前行的动力与勇气。