从“多”到“优”有多远——以“组合图形的面积”教学为例

江苏南京市长江路小学（210000）

在课堂中，尤其是在有关运算律的课上常常听到教师问“你喜欢用哪种方法？”“为什么会选择用这种方法？”等问题，这其实就是教师在算法多样的基础上组织学生进行算法优化。下面就以“组合图形的面积”的教学为例，谈谈我对“算法优化”的思考和探索。

一、求“多”：开拓思维，张扬个性

课始，教师出示图1，让学生在图中画出辅助线，探索图形的面积。

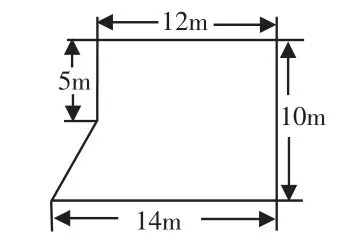
图1

在学生探索后，组织学生交流不同的解题方法（如图2）。

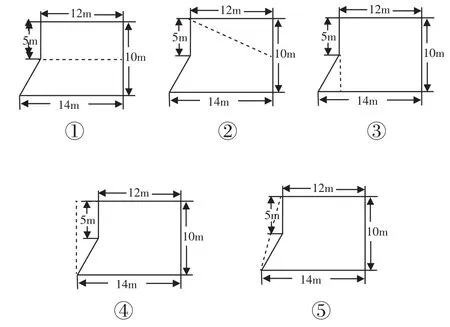
图2

教师引导学生将以上五种方法进行分类：方法①②③为“割”的一类，方法④⑤为“补”的一类。

这就是一个算法多样化的过程，此间学生充分地思考、交流，每一种方法的呈现都是一次思维的开拓。更重要的是，不同层次的学生都经历了探索的过程，从而发现算法，教师再对每一种思路、每一种算法都给予肯定，然后通过集体的力量对呈现的算法进行分析、比较和归类，使学生感悟算理，并且参与到教学过程中，体现了学生在课堂中的主体性。

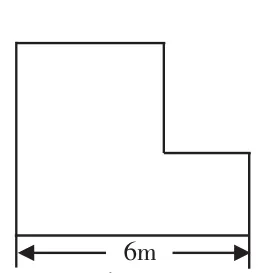
图3

二、求“优”：从善如流，聚焦本质

教师出示图3，要求学生用两种方法计算图形的面积。

以下两种是大多数学生采用的方法。

图4

师：只有这两种方法么？

生1：还可以把它分割成两个梯形来计算。

生2：也可以把这个图形补成一个长方形来计算。

师：没错，那为什么大家都选择这两种方法呢？

生1：这样需要计算的少。

生2：这两种方法都是把图形分割成两个长方形，计算简便些。

生3：这两种方法，既算得快，也不容易算错。

师：你们说的都很有道理，在计算时要尽量优化算法，选择合适的方法，以提高计算的速度和正确率。

教师没有刻意要求学生用某种所谓简便的方法进行计算，而是让他们自主选择两种方法来计算，大多数学生都选择了相对简便的方法，说明学生在面对多种解题思路时，已经具备了初步的优化算法的意识。当然，最优化的算法不能简单地由教师、教材、优等生等“权威”来规定与统一,也不能向学生机械灌输，而是应该把选择的主动权交给学生,引导他们去比较和感悟，“优化”应由学生说了算，不是教师说了算。优化算法是学生不断反思、不断完善的过程，是学生的思维水平不断提升的过程。在出现多种算法后，如果不及时进行对比从而优化，学生的思维可能会混乱，无法达到提升思维水平的目的。

三、求“中”：辩证思维，提升素养

一节课40分钟转瞬即逝，但却留下了很多问题，比如既有算法多样化也有算法优化，那二者是怎样的关系？该怎样处理？如何让学生学会数学地思考，感受优化的价值，让“算法优化”自然、自主地发生呢？

1.明确“算法多样”与“算法优化”的关系

算法多样化是指鼓励学生用多种多样的方法进行计算，使学生具有开放的思维和意识。算法优化是指根据学生的认知特点以及学生擅长的计算思维方式，引导学生强化某种思维运算方式，在原有基础上进行优化运算。有人认为两者是对立的关系，也有人认为两者是递进的关系。其实，从本质上看，两者之间并不矛盾，都是学生需要的，关键是如何把握其中的“度”。就这节课而言，让学生感受组合图形面积的算法多样性，能为学生的算法优化提供基础，然后再组织学生进行算法优化，这样循序渐进，符合学生的认知特点。因此，教师在课堂教学中要坚持算法多样化，也要坚持算法优化，站在学生思维的角度把两者有机结合起来，使二者相辅相成。

2.合理把握优化时机

在优化算法的过程中，要加强学生间和师生间的交流，这样，学生才能从对比和碰撞中感悟寻找最优算法的必要性，所以课堂上优化算法的时机选择尤为重要。比如先让学生讲解自己探索的求面积的方法，激发学生探索的欲望，然后师生间进行平等对话和交流，教师引导学生在理解每种算法的基础上再一次选择和思考，这样的教学既突出学生的主体地位，也符合学生的认知规律和心理特点。如果教师“要求统一用这种方法来计算”，那如此简单粗暴的“优化”方式是无法帮助学生内化知识的，也无法获得学生的认可。另外，恰当的优化时机才能促进学生数学思维的发展。在大部分学生选择了将图形分割成两个长方形的方法后，教师引导学生将这两种方法与其他方法进行对比和筛选，学生通过自己的思考敢于选择、学会选择，同时也学会了放弃。可见，让学生参与到优化的过程中来，能够培养学生分析和解决问题的灵活性，让每一个学生在自主优化的过程中发展数学思维。

3.相机应对优化生成

在实际的教学中，教师不可能预见课堂上发生的所有情况，所以要具备能根据当时的具体情况，巧妙合理地做出相应变动的能力。教师需动态把握学生在优化算法的过程中出现的“生成”，对于学生自主探究得出的多样化方法，首先给予充分肯定和鼓励，使学生体验到自我价值，增强学习信心；对于学生“创造”出的“另类”方法，比如将这个组合图形分割成3个甚至是4个基本图形来计算面积，就需要教师及时引导，避免引发学生的“创造疲劳”。