承前启后，搭建导入正比例意义教学的桥梁

江苏徐州市铜山区黄集镇金楼小学（221100）

导入是连接旧知和新知的桥梁，一端牵着来源，另一端指向未来。导入要成功，就要贯通前后，使之畅达。学习“正比例的意义”之前，学生已经掌握了“比和比例”，接触了大量常见的有关比的数量关系，因此，构建正比例意义是新授课的目标。那么，怎样导入才能贯通前后？

一、观察数量寻找变化关系

正比例反映的是两个数量之间的关系，教师要提供大量相关数组，引导学生通过观察分析找出对应关系。由于教学理念的差别，采用的素材也有些许差异，以下三种导入方式各有侧重。

【导入1】从一组数据入手

师（出示一袋糖果）：假如糖果每袋3元，可以推测出哪些新信息？

根据学生发言列表：

…………糖果/袋总价/元1 3 2 6 3 9 4 5 12 15

师：想一想，采购糖果的袋数与总价之间是什么关系？

生1：总价会随着糖果数量增加而增多。

师（追问）：什么是固定不变的？

生2：单价固定不变。

（教师根据学生的回答，写出比值，指出比值不变的两个量成正比例关系）

采用一组数量“开门见山”，能简短有力、直观快捷地揭示正比例的意义，但是一组数据具有偶然性和特殊性，说服力不足。

【导入2】多组数据导入

师（出示三组数据）：先观察，然后根据规律填表。

（1）太阳能热水器中水位高度和注水量对比情况

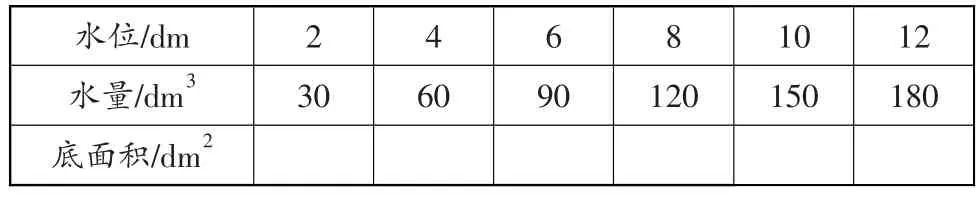
4水位/dm水量/dm3底面积/dm2 2 6 8 30 60 90 120 10 150 12 180

（2）动车里程表

时间/时里程/km 2 3 4 5 6 7 300 450

（3）商场的商品销售额

核桃/kg总价/元12 240 11 220 10 9 8 7

师：以上数据有什么相同之处？

学生观察后能够发现每组数量均涉及自变量和因变量，因变量随着自变量变化而变化，从而概括出正比例的概念。这样多数据的导入虽然花费的时间较多，但是由较多数据提炼出概念，更具说服力和信服力。

二、从图像中寻找变化

数学是研究现实世界并服务于现实世界的。导入1和导入2只是在数据理论里打转，没有与现实世界联系起来。下面介绍通过图形来引入的导入方式。

【导入3】由实验统计图导入

1.在操作与思考中引出相关联的量

师：往一个量杯注水。量杯的容积为400 mL，底面积为20cm2。随着水位的上升（用刻度尺量出高度），水面示数不断增加。水位每升高5厘米记录一次水量，然后绘制统计图。

师：水位高低与水量有什么特定关系？

2.在猜想与操作验证中形成图示

师：将注满的400mL水倒入另一个口径较小(底面积为10cm2)的量杯中，重复上述操作。

师：换了量杯后，水位高度与水量之间的变化情况相同吗？

（教师同步演示数据分析统计图）

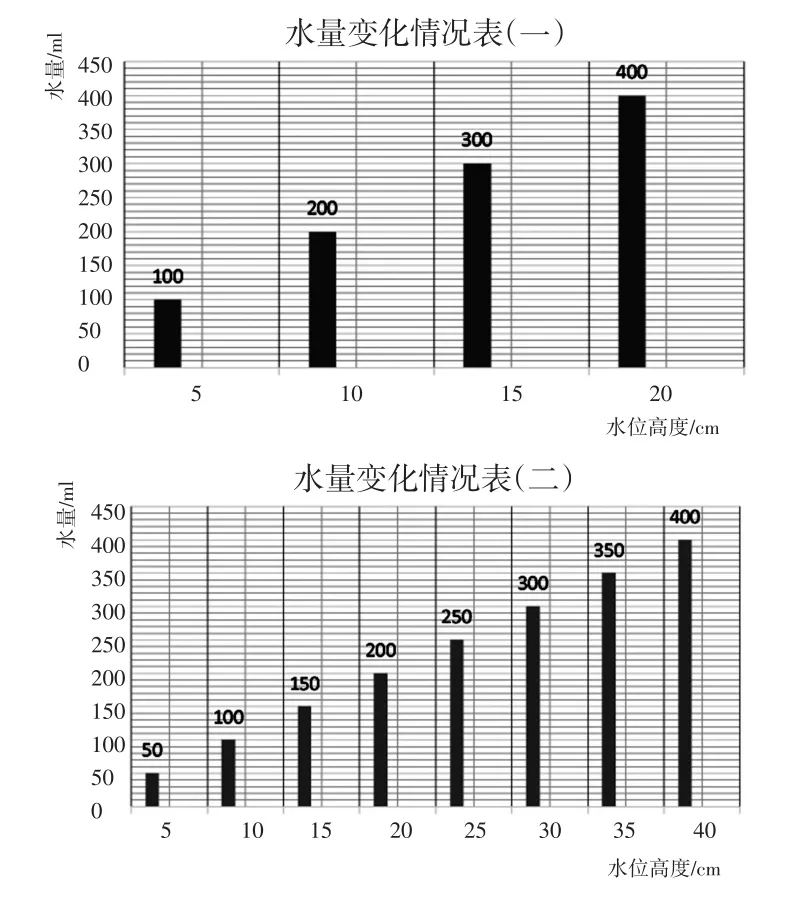
3.抽象成折线统计图

教师将柱状图转换成折线统计图，引导学生研究自

变量和因变量的数量关系，从而概括出正比例概念。

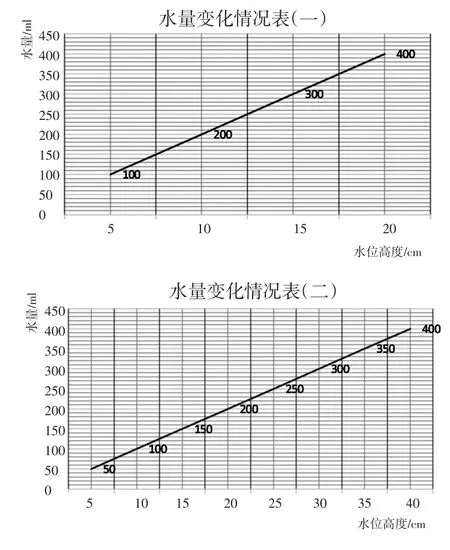
从实验操作导入，用物理变化过程实景展现数量变化的过程，是利用学生的生活经验为数据研究注入活力。

三、自由发挥寻找变化

自由发挥，就是摒弃具体素材，只提供想象情景。

【导入4】

师：今天我们学习正比例。这个概念很简单，经过自学就能知道什么是正比例关系。

1.阅读课本后完成习题：

课本选取的是（ ）和（ ）两个量来阐释正比例关系。其比值固定为（ ），物理意义为（ ）不变。

课本上是如何定义正比例的？

2.你能自己赋值并加以说明下表中两种数量之间的关系吗？补充数据后，说一说为什么这两个量可以构成正比例关系。

（1）一列动车里程表

时间/时路程/km

（2）工作时间与任务量的比值

时间/（）总量/（）

第2题的第（2）小题的解答过程实质上就是一个模仿过程，让学生依葫芦画瓢，模拟出两组呈正比例关系的量，而表格具备一定的开放性。这种导入方式正是“以学定教”教学理念的生动体现。

综上所述，尽管正比例教学的导入五花八门，但万变不离其宗。因此，在设计教学导入时，教师首先要弄清楚学生的最近发展区，此区段里有哪些知识要领；接着，明白学生的知识走向，充分预计存在的风险，然后一步步打通关隘；最后因势利导，因材施教，制定出科学合理的导入方案。换言之，教学导入应有理有据。