没有想象空间的操作活动是不完美的——“认识公因数和最大公因数”的同课异构

江苏泰州市智堡实验学校（225300）

在一次市级数学教研活动中，两位教师对同一课题“认识公因数和最大公因数”进行了同课异构教学。在介绍“公因数”概念时，两位教师都别具匠心，精心组织了操作活动——用“小正方形密铺长方形”，从而引导学生总结出“正方形边长必须同时是长方形的长和宽的因数才能完美密铺”，进而正式给公因数下定义，但是不同的活动安排带来了不同的教学效果。

【A教师教学片段】

师：音乐室地板是一个长30dm、宽20dm的矩形，由于地砖老化，现在要进行重装，有边长4dm和5dm两种规格的正方形瓷砖备选，请问哪种正方形瓷砖合适？

生（齐）：选用边长5dm的，因为5同时可以整除20和30。

师：请动手画一画，模拟铺一铺。

（学生动手操作，在用边长4dm的方砖密铺时感到为难；教师组织学生交流，讨论沿长排列几块，沿宽排列几块）

展示学生作品：

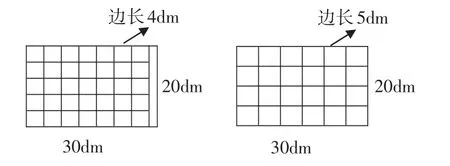
师:为什么边长5dm的方砖能正好密铺，而边长4dm的方砖则不行？

生1：主要是30dm那条边不能被完美分割。换言之，4不能整除30，而5既可以整除20又可以整除30。

师：除了边长5dm的方砖，还有哪种规格的方砖也可以密铺？画一画，填一填。

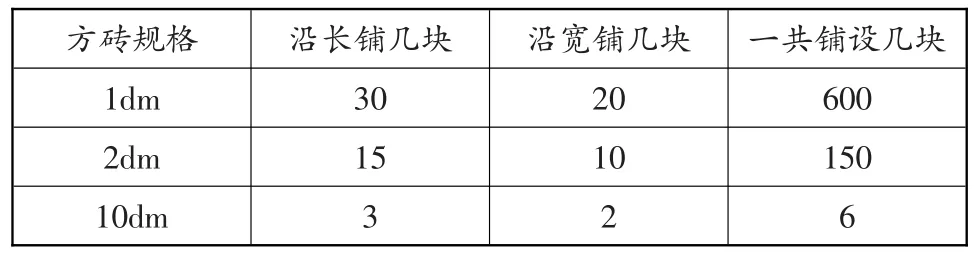
一共铺设几块600 150 6方砖规格1dm 2dm 10dm沿长铺几块30 15 3沿宽铺几块20 10 2

师：为何边长1dm、2dm、10dm的方砖也可以做到密铺？

生2：1、2、10和5一样，既是20的因数又是30的因数，是20和30的公因数。

（教师由此揭示“公因数”的概念）

【B教师教学片段】

师：分别用边长9cm和4cm的正方形纸片密铺一个长18cm、宽12cm的长方形，观察实验结果。

展示学生作品：

师：为什么不可以密铺？

生1：边的长度要是9或者4的倍数才可以。

师：请用数据说话。

生2：9是18的因数，但不是12的因数；4是12的因数而非18的因数。

师：密铺对边长有着严格的要求。

师：什么样的条件才能做到密铺？

生3：小正方形的边长要同时是18和12的因数，可以是1cm、2cm、3cm、6cm。

师：先拿边长6cm的正方形纸片做实验。

出示图：

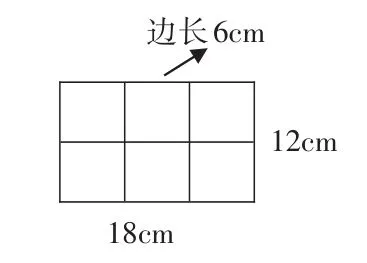
生4：6是12和18的公约数。

（教师用其他数据分别做实验，训练学生规范地表达“几是12和18的公约数，所以可以完美密铺”的句式）

两位教师的教学都经历了“操作—验证—思考—交流”的程序，也体现了“数形结合”的思想——借助长和宽同时完美分割密铺来导入“公因数”的概念。现对两位教师的处理方法进行逐一分析。

一、操作简约化，概念更深刻

A教师组织的密铺活动“用边长4dm和边长5dm的方砖密铺长30dm、宽20dm的音乐室地板”，共计需要用到方砖35或24块，长度差距太大，操作耗时过长。同时，操作要求是“全覆盖”，更加浪费时间。后续提问“沿长排列几块，沿宽排列几块？”也或多或少地对公因数概念的提出产生阻挠作用。学生初步形成“公因数”的概念雏形后的第二次操作活动“还有哪些规格的方砖可以密铺？画一画，填一填。”中，由于边长1dm和边长2dm的方砖全覆盖时数量太多，学生纠结于块数，而淡化了边长，削弱了“公因数”概念的准确性。

B教师组织的活动是“分别用边长9cm和4cm的正方形纸片密铺长18cm、宽12cm的矩形”，边长9cm的方片只需2块，边长4cm的方片只需12块。数量少，效率高。在铺的过程中，学生能直观地感知到“9”可以铺满“长度18”而不能铺满“宽度12”；“4”不能铺满“长度18”，却可以铺满“宽度12”。前后反差，集中反映出“正好铺满”长方形的关键在于“正方形的边长是否都是长与宽的因数”。显然，灵活应用“数形结合”的思想，就能用直观的几何揭示抽象的数字性质。随后教师在学生独立思考问题“什么规格的正方形才能正好铺满这个长方形？”时，组织学生尝试用边长6cm的正方形验证，学生通过操作证实了自己的设想。

二、想象和表达齐头并进

A教师的教学是通过能否铺满来举证是否是公约数，但是在用“边长1dm”和“边长2dm”的小方块密铺时，学生的主要精力和思维焦点集中在算块数上，而一个需要300块，一个需要150块，这样的“操作”严重阻碍学生思维，很是赘余。此处可以稍加改进，让学生选择想象或计算的方式，探究哪些方块可以密铺，这样就简单易行，更具含金量。

在B教师的教学中，学生经历两次操作后，已经基本理解“公因数”概念。教师可以适时布置想象推演活动：“边长3cm的正方形能否密铺？请想象图景。”“边长2cm或1cm的正方形能否密铺？请你边想象边描述。”学生凭借操作经验可以做到合理想象、清晰思考和准确描述。交流时，教师再“由扶到放”，不断诱导牵引，就能使学生的认识从懵懂感觉到清晰表达，实现思维和语言表达能力的双向提升。

综上，A教师把“操作发现”看作“揭示规律”的唯一路径，没有发掘学生的主观能动性，在学生表达不规范的地方并没有因势利导，而是生硬转折。B教师则把准了学习起点，操作时，将长和宽分别密铺，凸显了“正好铺满”的充分条件，而“公因数”概念的导入也正好建立在长和宽同时能够密铺的前提下，可以说是相当完美的操作活动。