逻辑齿轮弯曲强度研究
盛 伟,冯占荣,王利霞,邹 濛,王文轩
(南昌航空大学 航空制造工程学院,江西 南昌 330063)
0 引 言
对于渐开线齿轮弯曲应力的分析,一般将载荷Fn分为Fncosλ和Fnsinλ两个分量,因剪应力和压应力较小,所以主要计算Fncosλ分力产生的齿根弯曲应力,并通过修正系数来降低此计算带来的误差[1]。而对于逻辑齿轮而言,目前对于齿根应力的研究还处于利用分析软件计算最大应力分布情况。鉴于直齿轮的外载荷作用于与端面平行的平面内,并沿齿宽方向均匀分布,可将其简化为平面应力问题,冯显英等人[2]利用ANSYS分析软件在距离齿顶1 mm处施加载荷,研究表明最大应力发生在齿根的过渡曲线处;黄康、赵韩等人[3-4]考虑到轮齿刚进入单齿啮合区时,齿根所受弯矩最大,所以他们在节点以上的齿顶部分选择几个不同的点施加集中力利用COSMOS/M有限元分析软件计算轮齿弯曲应力。刘德平等人[5]以单对齿在节点处啮合分析不同齿根曲线对逻辑齿轮弯曲应力的影响。
根据文献[1],轮齿在齿顶处处于双对齿啮合状态时,两对齿共同分担载荷,此时齿根处的弯曲应力并不是最大的,当载荷作用于单对齿啮合的最高点时,齿根处的弯曲应力最大逻辑齿轮单对齿啮合的最高点的求解方法不同于渐开线直齿轮(主要是因为逻辑齿轮的齿形参数比较特别,如无确定的基圆半径、存在初始压力角和相对压力角等),通过对逻辑齿轮副的啮合过程分析,并以齿轮齿条啮合模型简化了啮合线的求解过程,推导了逻辑齿轮的啮合轨迹,并由此确定单齿啮合的最高点位置。然后以齿轮加载轴有限元分析方法[6]研究齿根弯曲应力分布情况并分析了齿形参数(初始基圆半径)对其的影响。
1 啮合过程分析
1.1 啮合过程
分析逻辑齿轮的一个轮齿的单侧齿面从开始啮合至结束啮合的过程来研究单个齿啮合最高点的位置。如图1所示,主动轮逆时针转动,从动轮顺时针转动,轮齿 2 的左侧齿面的从开始啮合到退出啮合,其中包含4个临界位置(8个临界啮合点)和3个啮合过程。

图1 逻辑齿轮啮合过程
图1(a)表示轮齿2在其左侧齿根处与从动轮齿顶A点处开始啮合;图1(b)表示轮齿1在其左侧齿顶C点处即将退出啮合状态;图(c)表示轮齿3在其左侧齿根F点处与从动轮的齿顶刚开始进入啮合状态;图(d)表示轮齿2的左侧齿顶G点处即将退出啮合状态。
从a位置到b位置的过程中轮齿1、轮齿2均与从动轮啮合,在轮齿1的左侧齿面在逐渐退出啮合状态时,轮齿2逐渐进入啮合状态,此时轮齿2上的啮合点在左侧齿面上从齿根向节圆位置慢慢移动。啮合点C表示轮齿2左侧齿面在齿轮副啮合中的双齿啮合的最高点。
从b位置到c位置的过程中,主动轮只有轮齿2参与啮合,当轮齿2左侧齿面上的啮合点达到最高啮合位置时(将退出啮合),轮齿3的左侧齿根处开始进入啮合状态,啮合点E表示轮齿2左侧齿面在齿轮副啮合中的单对齿啮合的最高点。
从c位置到d位置的过程中轮齿1、轮齿2均与从动轮啮合,在轮齿2的左侧齿面与从动轮逐渐退出啮合状态时,轮齿3左侧齿面上的啮合点从齿根向节圆位置慢慢移动。啮合点G表示轮齿2左侧齿面在齿轮副啮合中的双齿啮合的最高点。
1.2 啮合轨迹线的求解
逻辑齿轮的啮合轨迹线可以通过求解逻辑齿条与逻辑齿轮的啮合点并加以曲线拟合得到。由欧拉-沙瓦里公式可得,逻辑齿轮各个逻辑点的曲率半径分别与逻辑齿条上啮合对应逻辑点相同,那么一个齿条加工出的两个相啮合的齿轮的齿廓曲线上分布着曲率半径相等的对应逻辑点,曲率中心分别在各自的节圆上,按照标准中心距安装的逻辑齿轮副对应啮合的逻辑点都通过节圆的公切线,且曲率半径相等,且啮合点的公法线通过两节圆相切的节点[7]。
建立坐标系,如图2所示。以两节圆相切的节点为原点建立啮合线的坐标系。此时的啮合逻辑点在坐标系中的坐标为:
(1)
依据式(1)利用MATLAB计算出逻辑点在啮合时的坐标,并将其导入到CATIA进行曲线拟合,并构造如图1(c)所示的啮合位置的逻辑齿轮副,测量E点在主动轮上的半径值,即单对齿啮合最高点位置。

图2 逻辑齿轮单对齿啮合最高点示意图
2 齿根应力有限元分析
2.1 前处理
根据圣维南定理,齿轮传动过程中,单个齿在轮体径向的影响范围约三个齿,在超出这个范围后,应力就变得很小[8]。同时考虑到逻辑齿轮的形成是基于逻辑齿条,逻辑齿轮毛坯通过与逻辑齿条范成运动生成逻辑齿轮。同条件下,就弯曲强度而言,单圆角齿条刀具对应齿根过渡曲线的逻辑齿轮比双圆角齿条成形的逻辑齿轮好。所以以单圆角齿条刀具成形的逻辑齿轮的三齿模型为研究对象,如图3所示。
逻辑齿轮除了与渐开线齿轮的共有参数外,与逻辑齿条齿廓线相关的参数有:初始基圆半径G0、初始压力角α0、相对压力角δ等[9]。笔者选用的模型参数如表1所示。根据经验公式,基圆半径变化规律取Gi=G0[1-sin(0.6αi)]。

表1 模型参数列表
选用齿轮加载轴有限元分析方法对逻辑齿轮的齿根弯曲进行分析,由上节中确定的最高啮合点(逻辑点),该点处的压力角可以通过作图的方法(简称图解法)获得,也可以通过MATLAB程序计算出逻辑点所对应的压力角。建立齿轮加载轴模型,如图4所示。

图3 逻辑齿轮三齿模型

图4 逻辑齿轮加载轴建模
在Workbench静力结构分析中,齿轮材料选用结构钢,对于模型的网格划分,采用扫掠式网格划分方法,定义单元大小为1 mm,并对齿根处的的网格进行细化,划分结果如图5所示。对加载轴的长方形表面施加固定约束,对齿轮的内孔表面施加圆柱形约束,只保留圆周方向的自由度,最后在内孔表面加载800 N·m的力矩。

图5 模型的网格划分
2.2 后处理
利用ANSYS Workbench软件分析逻辑齿轮所受的最大主应力,结果如6所示。
从图6中可以看出逻辑齿轮的弯曲应力主要集中在齿根处,并且对于同载荷工况下不同初始基圆半径齿条所产形的逻辑齿轮,所对应的齿根应力有所不同,从这三个数据可以看出,初始基圆半径取10 000 mm时逻辑齿轮的弯曲强度最好,这为逻辑齿轮从齿形参数方面优化设计提供了参考。
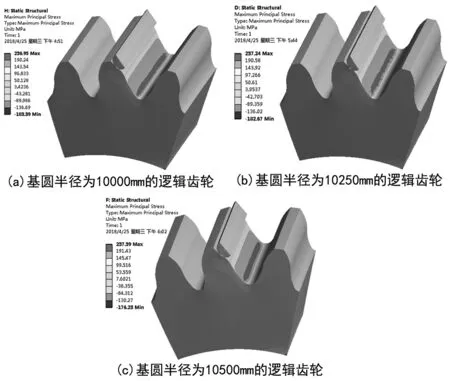
图6 逻辑齿轮弯曲应力图
3 结 论
(1) 结合逻辑齿轮的齿形特点,分析了一对齿的单侧齿廓线啮合的过程,并推导啮合线的方程,根据啮合的临界点位置,确立单对齿啮合的最高点所处的位置及载荷作用角。
(2) 利用齿轮轴加载有限元分析方法,可真实地模拟逻辑齿轮承受载荷时的受力情况。并分析逻辑齿轮齿形参数初始基圆半径G0对齿根弯曲应力的影响,有助于从齿形参数层面上优化逻辑齿轮的设计。

