汽车排气系统吊耳动刚度的响应曲面优化
李 壮,胡海峰,王家璇
(华中科技大学 机械科学与工程学院,湖北 武汉 430074)
0 引 言
汽车排气系统与发动机排气口连接,通过主、被动吊钩和吊耳悬挂于车辆底部。发动机工作时,振动由发动机传递给排气系统,再由排气系统传递给车底板。吊钩形状位置、吊耳刚度特性的选取影响排气系统的振动特性,进而影响了整车的NVH性能。
研究表明,生产设计过程中,吊钩吊耳能影响排气系统振动特性。吊钩需要选择合适的布置位置,可由平均驱动自由度位移法结合车底板结构确定;与之配合使用的吊耳则需要选取合适的动刚度值,目前主要考虑吊耳静变形、所受的最大静拉力、以及传递到车底板的最大动载荷作为衡量的标准。若吊耳动刚度选取过小,虽然隔振率会有所上升,传递给车底板的载荷会减小,但吊耳静变形会增大,更容易疲劳,使用寿命下降;若吊耳动刚度选取过大,则虽然静变形和疲劳性能满足了要求,却由于吊耳选得过“硬”,隔振效果则会变差,降低乘用者的舒适体验。所以在选取吊耳动刚度时要综合考虑这些因素[1]。
目前应用较广泛的优化方法是正交优化或遗传算法优化,以吊耳静变形之和、动态反力极值之和最小为优化目标,有的则是再加上动态反力极值的标准差和静拉力的标准差最小化为目标进行稳健优化[2-3]。采用响应曲面法来优化吊耳动刚度,选取满意度函数模型,将设计方的疲劳性能、隔振性能等各种要求综合考虑。用所拟合的函数模型代替有限元分析,能很大程度上的缩减计算时间,降低成本。响应曲面法自提出以来,经过不断的发展,被广泛应用于各行各业,在解决工程优化设计问题时,响应曲面法同样不失为一个好的选择[4-6]。
1 响应曲面优化
响应曲面法的原理即设计合理的试验,获取一系列设计变量与响应的数据,对这些数据进行曲线拟合,建立合适的数学模型来体现二者之间的关系。
y=f(x1,x2,x3,…)+ε
(1)
式中:x1、x2、x3为设计变量;ε为误差项;y为响应。通过该数学模型求解最优解,找到能得到最接近目标的响应时的设计变量组合。
采用中心复合设计,通过有限元分析得到一组实验数据,构建每一个单响应关于设计变量的响应曲面;进行多目标优化时,选择一种满意度函数方法来综合考虑不同响应的不同重要程度的要求。
1.1 汽车排气系统有限元分析
根据企业提供的物理模型,进行有限元建模。用壳单元对排气管道等薄壁件进行建模;对法兰,主、被动吊钩等进行实体建模;用三向弹簧阻尼单元(body to body)代替波纹管和吊耳;将动力总成等效成质心处的质点,左悬置、右悬置、后悬置等效成三向弹簧阻尼单元(body to ground)。有限元模型如图1。图1所示排气系统材料属性及刚度参数如表1、2所示。

图1 排气系统有限元模型(图中编号为吊耳编号)

表1 图1中所赋予的材料参数

表2 悬置刚度参数表 (N/mm)
为了防止在使用过程中排气系统与其他部件发生碰撞,需要限制吊耳的静变形量;考虑到吊耳的使用寿命,需要对其承受的静拉力进行限制。对建立的有限元模型进行静力学分析,在重力作用下,分析每个吊耳的静变形和所受的静拉力。选用的吊耳材料在所考虑的频率范围0~200 Hz内,其动、静刚度之比可近似看做2:1。某初始方案静变形及静拉力分析结果见表3。
为了保证车辆的乘坐舒适性,需要尽可能降低且均衡各吊耳传递到车底板的动态反力,减小被动端振动加速度,提高吊耳隔振率。对建立的有限元模型进行谐响应分析,在发动机扭矩激励下,分析每个吊耳的动态反力。按照行业标准,施加100 N·m的激励力矩于动力总成质心处,方向绕曲轴,频率范围为5~300 Hz。各吊耳传递到车底板的动态反力如图2,且约束模态频率避开了发动机怠速频率22~35 Hz,未发生耦合。

表3 初始方案静力学分析结果

图2 吊耳传递到车底板的动态反力
1.2 响应曲面优化模型
要对吊耳动刚度进行优化组合,故选取六个吊耳的动刚度值作为设计变量:
X=[x1,x2,x3,x4,x5,x6]T
=[k1,k2,k3,k4,k5,k6]T
(2)
式中:k1、k2、k3、k4、k5、k6为六个吊耳的动刚度值,N/mm。采用二阶模型来描述每一个单响应与设计变量的关系:
(3)
按照生产要求,其中静变形Si希望以3.5 mm为中心值,在3~4 mm范围内为合格;各吊耳的动态反力极值Fi则希望尽可能小;给定动刚度值选取范围14~30 N/mm,且静拉力ni不超过50 N。则有以下约束条件:
(4)
需要优化的响应有多个,结合要求,采用望小型和望目型两类满意度函数[7]。每一个静变形响应可采用望目型来描述满意度:
(5)
式中:dj(Si)为满意度,j∈[1,6];Tj、Lj、Uj分别为响应的目标值、下限、上限;w1、w2为权重。每一个动态反力极值响应可采用望小型来描述满意度函数:
(6)
式中:dj(Fi)为满意度,j∈[7,12];w3为权重。满意度函数如图3所示。
根据各响应结果并按要求确定每个响应的权重wj和重要度pj,应用加权几何平均将多响应合成为单响应:
(7)
将D作为整体满意度函数,即目标函数。求使该函数取得最大值的设计变量组合即为最优的动刚度组合。

图3 两种满意度函数及权重的影响
1.3 优化结果
在建立了每个单独的响应曲面后,按上述目标函数及约束条件进行优化,得到当前条件下最优的一组刚度值,对比优化前后的结果,见表4,动态反力极值如图4所示。
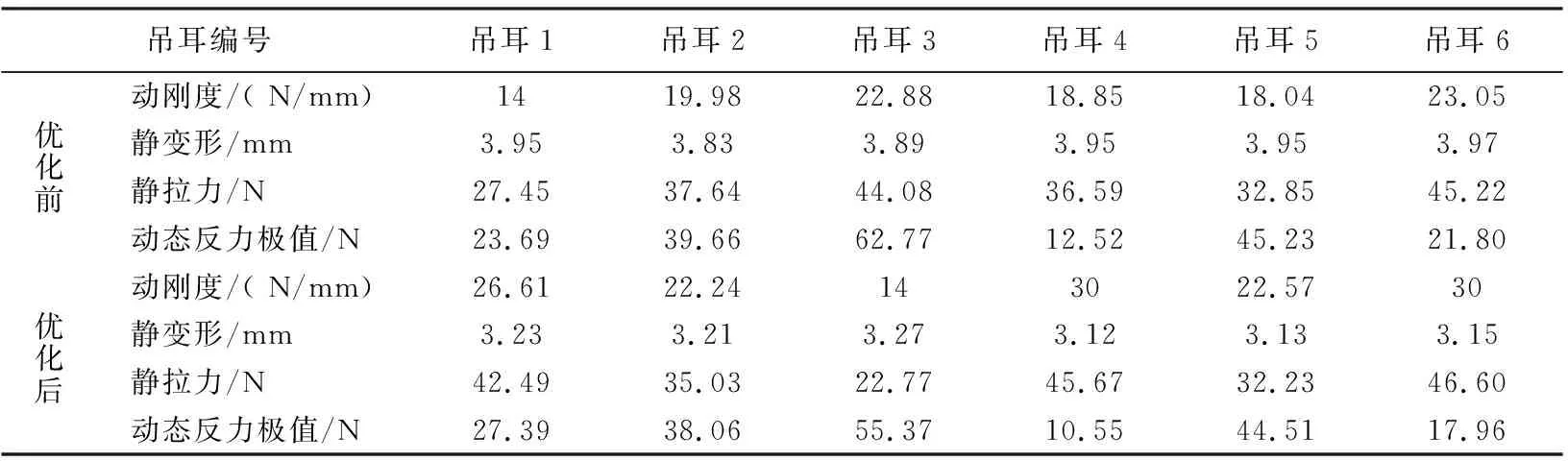
表4 优化前后分析结果对比
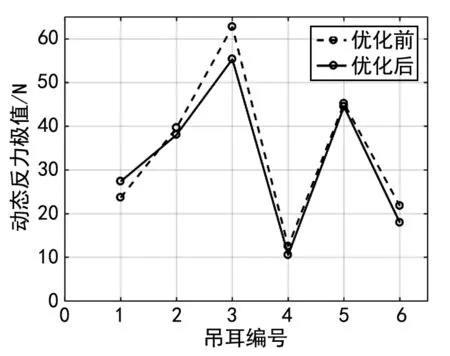
图4 优化前后各吊耳动反力极值
相对于初始方案,优化后在满足吊耳静变形和静拉力要求的同时,动态反力极值大部分都降低了。可见优化后的动刚度组合要优于原组合。
2 结 论
采用响应曲面法对汽车排气系统的吊耳动刚度组合进行了优化,几点结论如下:
(1) 使用响应曲面法对汽车排气系统静力学、谐响应等复杂的有限元分析过程进行数学建模。在保证了拟合优度的情况下,能较准确地描述吊耳动刚度与静变形、静拉力、动态反力极值之间的关系,用来优化吊耳动刚度组合取得了较好的效果。同时该模型对解决一些后续相关的工程问题也有一定作用,能有效节省大量时间。
(2) 在将静位移、静拉力、动态发力极值等多个响应综合考虑时,采用的满意度函数法能够方便地对每个单响应赋予随具体要求所变化的权重和重要度。这样能够更贴合生产实际要求,而不是单纯的以标准差和均值来衡量优化效果,具有一定的兼容性。

