围尺法和光电测距法测量立式金属罐基圆半径的对比和分析*

梁艳争 姚新红 李雪菁 / 上海市计量测试技术研究院

0 引言

立式金属罐不仅是石油化工、食用油脂和液化天然气等行业的存储罐，经过计量检定后，可成为大宗液体货物贸易中重要的计量器具。我国计量监管中，立式金属罐计量结果不仅直接关系到有关企业的经营结算、成本核算、能源节约等各项经济效益，也直接关系到我国对外贸易的经济利益和国家计量信誉[1][2]。

目前，国内外立式金属罐的容量测量方法主要采用围尺法、光学参比线法、光电测距法等几何测量法。围尺法作为国际仲裁检定的标准方法，需要搭建脚手架才能完成，属于高空作业；光学参比线法需要人工拉动移动式径向偏差测量仪，这两者均存在劳动强度大、安全系数差、测量效率低等缺点[3]；光电测距法使用全站仪、扫描仪等精密测量设备进行测量，克服了以往立式罐容量计量方法存在的准确度低、高空手工作业、劳动强度大、工作时间长等不足，在立式罐容量计量领域中应用日益广泛，已经成为最常用的计量方法之一，特别是随着立式罐的大型化趋势发展，这种方法的优势更为明显。

然而在实际应用中，因光电测量设备在立式金属罐容量的计量应用中还有很多不足，其基圆半径测量结果仍需要与围尺法进行比对和分析。早在2002年，徐忠阳、张良琚、魏进祥最早使用基于全站仪设备的光电测距法与光学参比法测量结果进行了比较，数据显示光电测距法在合适的测量条件下能较好地实现立式金属罐基圆的半径测量[4]。2011年全国容量会议上，郭云霞、崔越、崔建和针对不同半径区间的立式金属罐的基圆进行了对比和分析，认为两种方法的半径测量结果存在系统偏差[5]。2012年，赵立、车齐荣、王冬针对几种典型规格的立式金属罐使用围尺法和全站仪的光电测距法进行了对比和分析，认为光电测距法与围尺法相比，基圆半径测量误差随半径的增大而增大[6]。上述文献对于基圆半径测量中光电测距法与围尺法均进行了试验和对比，验证了全站仪方法在立式金属罐容量计量中的可行性。

在立式金属罐容量检定中，基圆半径测量是最重要的基础数据，其测量结果的准确性对于容量计量十分重要。为更加科学地衡量围尺法和光电测距法的测量结果，本实验将一座典型的立式金属罐作为测量对象，采用基于全站仪的光电测距法和围尺法，测量该金属罐基圆半径。通过比较两种方法对基圆半径的测量结果及不确定度分析，从而判断两种方法在测量基圆半径中的一致性。

1 测量过程

选择一座标称容量为10 000 m3的立式金属罐，其外壁无明显凹凸不平的现象，基圆位置处罐壁及周围无明显影响测量的障碍物；罐内壁为清理过的碳钢材料，符合光电测距法和围尺法的测量条件。

1.1 围尺法

先绕罐查看第一圈板四周罐壁情况，将无明显障碍物，且距第一圈板焊缝300 mm处（第一圈板板高的3/4上下100 mm处）作为围尺的最佳选定位置。用色笔每隔1.0～1.5 m画出水平标记，作为围尺轨迹，并清除围尺轨迹上影响测量结果的杂物，以保证钢卷尺测量时贴紧罐壁。用磁性表座将钢卷尺的尺头固定，沿罐壁放尺，使尺带紧贴罐壁并大致围绕在围尺轨迹附近，用磁性表座固定5 min左右，使尺带与罐壁达到温度平衡，以消除尺带与罐壁的温差所造成的测量误差。用拉力计勾住尺头，将钢卷尺的零分度线与起点竖线重合，给尺带施加与尺检定状态时相同的拉力，同时观察尺带零分度线与起点竖线是否发生位移。用相同方法测量两次，两次测量结果的误差应不超过3 mm，否则需要重新测量。

使用Ⅱ级钢卷尺，采用上述方法测量该金属罐基圆外周长两次，分别为89 566.0 mm，89 568.0 mm，围绕第一圈板一周，合计共19条焊缝。查阅钢卷尺溯源证书报告，围尺所用钢卷尺在90 m处的长度修正值为4.8 mm。使用超声波测厚仪测量第一圈板平均板壁厚度为18.0 mm。因此，采用围尺法测得该罐的外周长：

该罐基圆内半径：

1.2 光电测距法

把光电测量设备全站仪架设在金属罐内底板的中心位置并调平，使用全站仪在基圆位置圆周均匀测量36个测量点。在测量过程中，人双脚及重心不得移动，避免人为影响设备水平状态。设测量出的36个测量点的坐标为（xi，yi），基圆拟合圆心坐标为（Am，Bm），使用迭代法，拟合出基圆半径Rm：

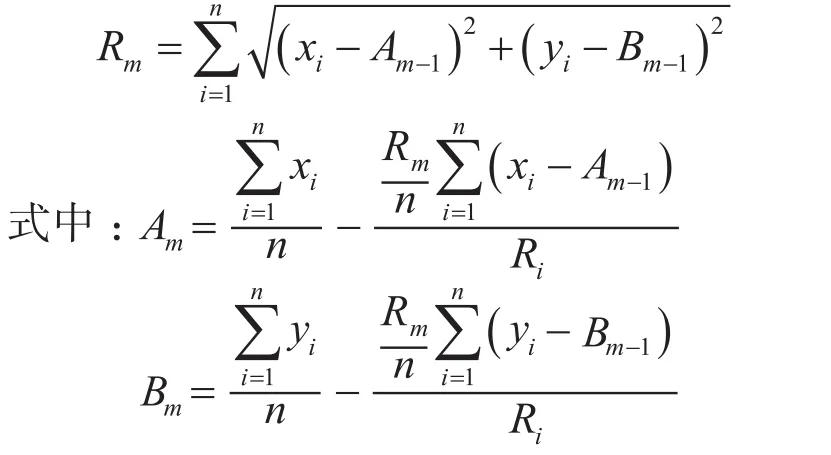
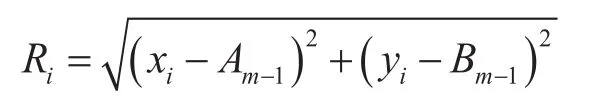
式中：Rm——基圆拟合半径；

xi——光电测距法测量点横坐标；

yi——光电测距法测量点纵坐标；

Am——基圆拟合圆心横坐标；

Bm——基圆拟合圆心纵坐标；

m——基圆拟合半径迭代步数；

n——基圆水平圆周测量点总数

通过设定初始值A0= 0，B0= 0，用迭代法计算Rm值，直至|Rm-Rm-1| ≤0.1 mm。

该金属罐基圆位置四周罐壁温度为29.2 ℃、29.0 ℃、30.3 ℃、29.6 ℃，平均温度t= 29.5 ℃，并经温度修正，基圆拟合内半径为R= 14 234.6 mm。

2 测量结果不确定度分析

2.1 围尺法测量基圆半径不确定度

围尺法测量基圆周长的数学公式为

C0=C01+C02+C03+C04

式中：C0——围尺法中基圆周长，mm；

C01——围尺法中钢卷尺示值，mm；

C02——围尺法中钢卷尺修正值，mm；

C03——围尺法中因拉力和定位引入的钢卷尺修正值，mm；

C04——围尺法中因跨越或焊缝等障碍物引入的钢卷尺修正值，mm

根据测量出的基圆周长，则基圆内半径：

式中：δ——第一圈板板壁厚度，mm

围尺法测量基圆半径不确定度来源包括：测量时钢卷尺示值引入的不确定度、钢卷尺修正值引入的不确定度、钢卷尺围尺时拉力和定位引入的不确定度、钢卷尺跨越焊缝等障碍物修正引入的不确定度、超声波测厚仪引入的不确定度等。

2.1.1 钢卷尺示值

钢卷尺示值的最大允差为±1.0 mm，服从均匀分布，则相应的标准不确定度为

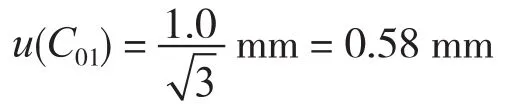
2.1.2 钢卷尺修正值

测量结果采用钢卷尺检定证书的修正值，该修正值来源于检定时的标准钢卷尺，经查阅检定证书，该标准钢卷尺的测量不确定度为0.12 mm （k= 2），则标准不确定度：

2.1.3 围尺时钢卷尺拉力和定位

圆周长测量最大允差为±3.0 mm，服从均匀分布，则相应的标准不确定度为

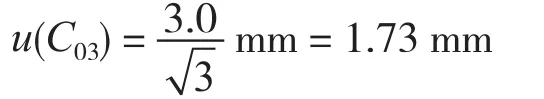
2.1.4 钢卷尺跨越焊缝等障碍物修正

最大误差为±1.0 mm，服从均匀分布，则相应的标准不确定度为

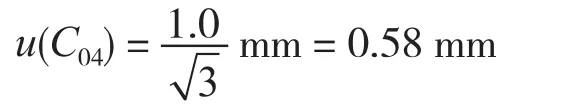
则基圆周长C0测量的标准不确定度为

2.1.5 第一圈板板壁厚度测量的不确定度

第一圈板板壁厚度测量过程中因分析测量仪器（超声波测厚仪）和板壁厚度不均匀引入的不确定因素，板壁厚度测量结果

δ=δ01+δ02

式中：δ——第一圈板板壁厚度测量值，mm；

δ01——超声波测厚仪测量示值，mm；

δ02——第一圈板板壁厚度不均匀引入的测量结果修正值，mm

超声波测厚仪的测量误差为±0.10 mm，服从均匀分布，则相应的标准不确定度为

考虑到板壁厚度的不均匀度为±0.40 mm，服从均匀分布，则相应的标准不确定度为

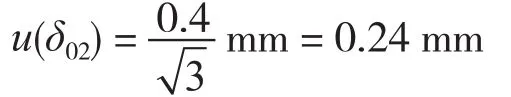
则第一圈板板壁厚度测量的标准不确定度为

2.1.6 基圆内半径的标准不确定度为

2.2 光电测距法测量基圆半径不确定度

基于全站仪的光电测距法测量结果通常以测量点坐标形式表示，全站仪测量原理如图1所示[6]。

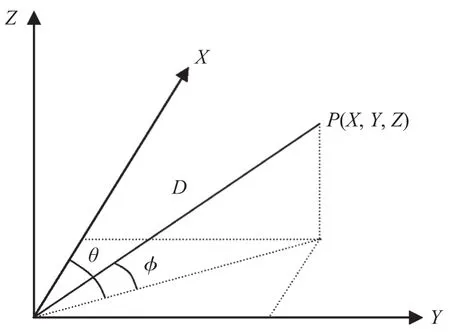
图1 全站仪目标点测量原理

式中：D——全站仪测量目标点时的斜距；

θ——全站仪测量时的水平角；

X、Y、Z——全站仪测量时目标点的坐标值

在基圆水平圆周测量拟合半径时，不考虑Z值，仅使用X、Y值。测量点坐标的X值的不确定度为

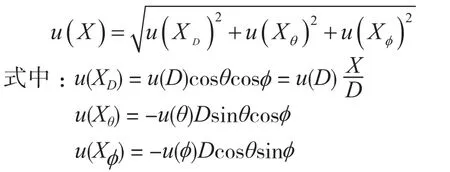
测量点坐标的Y值的不确定度为

基圆拟合半径的不确定度

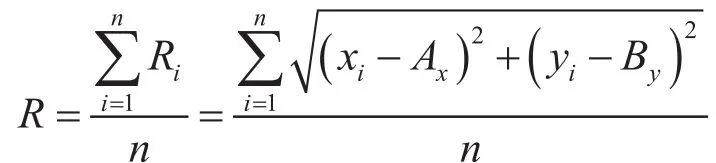
式中：n——基圆的测量点数；

Ax、By——拟合基圆的圆心坐标点

式中：Xi、Yi——基圆水平圆周测量点的坐标；

u(Xi)、u(Yi)——基圆水平圆周测量点的不确定度

设Ax= 0，By= 0，在基圆水平圆周测量拟合半径时，竖直角= 0，则基圆拟合半径的不确定度：

光电测距法测量基圆半径的主要不确定度来源为：全站仪测距、测角引入的不确定度，罐壁条件和半径温度修正引入的不确定度。

2.2.1 查阅全站仪检定证书，测距标准差为：固定误差a= 2.0 mm，比例误差b= 2.0 mm/km，k=2。本次测量基圆半径R约为14 234 mm，因此，全站仪测距引入的不确定度U（D）=（2.0 + 2.0×10-6R）=2.03 mm。根据经验，由于竖直角的振动，罐壁反射率不同引入的不确定度Ua= 2.0 mm，k= 2。因此，全站仪测量基圆时的测距不确定度：

2.2.2 根据全站仪检定证书，全站仪测角符合I级，测角标准偏差≤1.0''，则

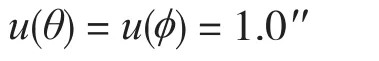
2.2.3 全站仪拟合基圆半径的不确定度：

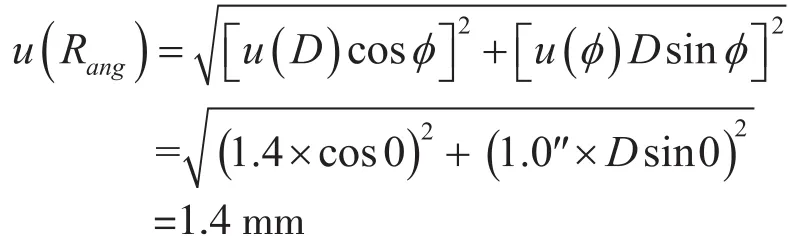
2.2.4 由半径温度修正的不准确引入的标准不确定度，由于测量罐壁温度所用辐射测温仪的最大允许误差为±1.0 ℃，罐体碳钢材料的线膨胀系数为：0.000 012 ℃-1，对于半径R= 14 234.6 mm，由温度测量误差所引入的区间半宽a= 0.17 mm。其为均匀分布，由半径温度修正的不准确引入的标准不确定度分量为

2.2.5 基圆半径的合成不确定度

3 两种方法测量的半径值比较

围尺法测量出的半径值Rw= 14 236.9 mm，光电测距法测量出的半径测量值R= 14 234.6 mm，两种方法的半径差：

因Rw和R是分别用两种不同的方法，即立式金属罐基圆半径进行测量，两者不相关，半径差ΔR的不确定度为

半径差ΔR的扩展不确定度

U(ΔR) =ku(ΔR) = 2×1.45 mm = 2.9 mm，k= 2

因ΔR

再以标称容量为1 000 m3、2 000 m3、5 000 m3的立式金属罐作为测量对象，分别用围尺法和全站仪测量基圆半径，对测量数据进行对比和分析，得出的结果与上述结果一致。

4 结语

本文选择一座10 000 m3立式金属罐，分别用围尺法和光电测距法对其基圆半径进行测量，并分别对各自测量结果进行了不确定度分析和评定，且对测量结果的一致性进行了评判，验证了光电测距法和围尺法在测量立式金属罐基圆半径结果的一致性。