精密成形磨削工艺参数的仿真研究
李志伟,张沭玥
精密成形磨削工艺参数的仿真研究
李志伟1,张沭玥2
(1.四川省机械研究设计院,四川 成都 610063;2.西南交通大学 机械工程学院,四川 成都 610031)
为研究精密成型磨削过程中工艺参数的选择,利用CAD软件建立摆线齿轮成型磨削三维模型,在Deform-3D有限元软件中设置相应仿真参数,仿真分析砂轮线速度、摆线轮进给速度对磨削后表面粗糙度、磨削力、材料去除量及砂轮磨损量的影响。结果表明:齿轮表面粗糙度随砂轮线速度的增加而减小,随摆线轮进给速度的增加而增加,随打磨次数的增加而减小;在进入成形磨满磨过程后,法向力峰值将会基本稳定在切向力峰值的三倍;随着进给速度增加,磨耗比存在波浪形起伏的变化。
成形磨;材料去除;表面粗糙度;磨削力;磨耗比
磨削是实现机械零部件表面形态和尺寸精确加工的极为重要的手段。从磨削原理而言,工作砂轮为圆柱砂轮时,砂轮磨削工作面上各磨粒具有相同的磨削速度、磨削压力和磨削深度,内外圆磨和平面磨便符合这种工况。平面磨削时由于砂轮母线是直线,所以只要提高磨削工件的接触刚度,修改砂轮线速度和切深等变量一般就可提高磨削质量。但以上方法并不适用于成形磨尤其是高精度成形磨,成形磨的砂轮不是圆柱砂轮,砂轮母线是一条曲线,磨削时母线上各点的磨削速度、磨削压力及深度都不同,实际完成的工件形状并不与砂轮母线一致。目前,砂轮选型、磨削参数等对磨削质量、效率及成本的影响并不清楚,并且受传感器、磨削副工作界面空间及磨削工作环境条件等诸多因素制约,现在还没找到很好的办法对砂轮磨削开展精确定量的动静态测量研究,很大程度上依赖加工经验。罗勇等[1]以某大型齿圈成形磨为研究对象,以变形控制为目标,对不同磨齿余量进行了磨削变形仿真,得到了较优的余量分配值。周涛[2]通过推导成形磨削中的磨削力计算公式,基于成形磨削的粗、精磨工艺正交试验,找出优化工艺参数,并对成形磨削进行温度仿真预测。杜晓阳[3]对砂轮的选择、成形砂轮的修整、磨削液和磨齿余量的选择等影响磨齿质量的因素进行了定性分析,为保证磨齿质量提供了理论依据。
本文通过有限元仿真研究方式对磨削工艺参数对成型磨削工件的影响进行研究分析,得出了成型磨削砂轮及磨削参数的相互关系,参数的变化趋势基本符合工程的实际经验,参数变动范围也较为接近。本文提出的研究方法已经可以对成型磨削工艺参数提出方向性指导意见,经进一步完善后可以作为成型磨削设计及工艺优化的有力工具。研究参考了西南交通大学摩擦所等单位在铁路轮轨磨削仿真研究[4]及摩擦试验测试方面的研究成果,在此基础上进行了拓展研究,从圆柱砂轮磨削拓展到成型磨削,圆柱砂轮磨削可以看成是成型磨削的特例。
1 基于实际工艺的成型磨削有限元仿真模型
从主导关系的本质上看,砂轮磨削的磨损机理是砂轮磨粒与工件界面金属组织之间的相互力学作用。在微观尺度上,磨粒具有在一定范围内分布的小曲率半径,工件表面界面形状是可以用粗糙度定义的具备统计特征的起伏地势,因此在接触点上具有很大的接触应力,远超过材料的强度极限,磨粒运动的过程中对金属表面材料挤压、拉伸、切割、撕裂,材料发生大应变,从而剥离部分金属,材料表面发生非线性的弹塑性变形,表面晶向随之产生畸变,产生残余应力,此即为磨削的微观机理。
Deform-3D是一套基于有限元的工艺仿真系统,用于分析金属成形及其相关工业的各种成形工艺和热处理工艺,在工作机理上与磨削具有相似性,故本文采用Deform-3D作为研究工具。
1.1 三维模型建立
砂轮一般是由结合剂和磨料(Al2O3、SiC、CBN、WC等)组成,在磨具内压成型后由树脂固化或在烧结炉内烧结结合而成,每个沙砾是由不同形状的尖锐多面体构成。典型沙粒形状如图1所示。

图1 砂砾形状示意图
除材料外,砂轮最重要的参数就是粒度,本文所参照的粒度标准如表1所示。
通过显微观察,沙粒主要形状接近六面体结构,本次仿真便以此形状建立了沙粒模型,并将所有沙粒大小按其粒度设置一致。当然这个设置也是计算误差的一个来源,但分析认为,从宏观来看不同沙粒形态由于与金属的接触概率和接触角不一样,所以沙粒的形状及其分布不同对磨削结果会产生一定影响,影响主要体现在磨削力及磨耗比上,这些因素可以通过后期试验校准的方式调整。
60#砂轮磨粒面密度约为7(个)/mm2,成形砂轮与摆线接触部分砂轮面积估算约为162 mm2(一个圆周长,=3 mm,=6 mm,=3×3×3×6=162 mm2)。磨粒服从随机分布,磨粒突出高度服从正态分布,生成随机分布点及正态分布点,确定磨粒放置的三维坐标,根据坐标手动放置磨粒后,手动调整磨粒使其所处的线密度是一致的,得到最终砂轮模型,如图2所示。
本例中选用摆线齿轮作为工件,将坐标点导入CAD中绘制出轮廓线,取起始齿及左右出入3%部位为齿轮模型草图轮廓线,将草图轮廓线导入三维CAD后拉伸至9 mm厚,得到最终摆线轮三维模型,如图3所示。
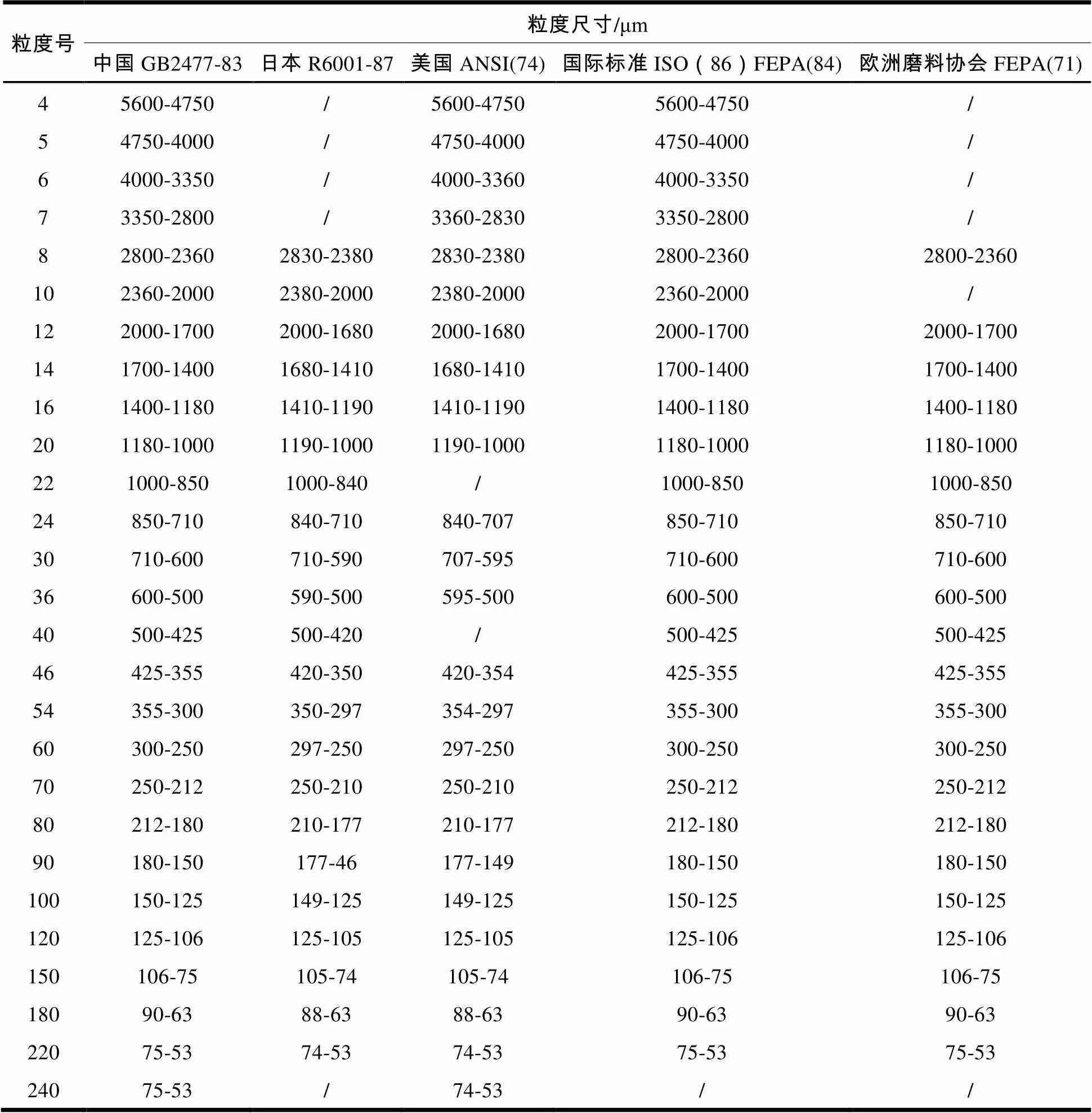
表1 中外磨料粒度尺寸参照标准
1.2 仿真参数设置
砂轮磨削的工艺参数包括砂轮材料、砂轮粒度、磨削线速度、磨削深度和磨削液,在本次仿真研究中没有考虑磨削液。传统工艺主是按照经验选择、最后通过试磨加工反复调整参数来最终完成选型和工艺参数确定。仿真研究则可以通过对工艺参数进行设置,通过软件评估效果,从而对工艺参数选择提供方向性指导,提高加工质量和缩短试磨加工的周期和成本。
本文中选取摆线齿轮材料为GCr15(热处理状态是调质+齿形表面淬火),砂轮磨料材料为Al2O3。采用Deform-3D有限元软件中自带的混合四面体单元进行成形磨削砂轮和摆线轮的网格划分[5],如图4所示。
为提高计算性能,本文选择共轭梯度法作为求解器。共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,共轭梯度法是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。其所需存储量小,步收敛性,稳定性高,而且不需要任何外来参数。
考虑到工件在磨削微观条件下磨损机理以黏结磨损为主,磨损模型选取Usui磨损模型,因其更适于处理类似金属切削的连续过程,且扩散是磨损的主要原因。

图2 砂轮三维模型

图3 摆线轮三维模型

图4 成形磨网格划分模型
Usui黏结磨损模型为:

式中:W为黏结磨损量,为正压力,N;v为磨削滑移速度,m/s;为温度,℃;A和B为磨损常数,参数取值来自磨损试验标定。
2 仿真结论与分析
2.1 仿真分析目标
磨削加工工艺最关心的是表面粗糙度、材料去除率与砂轮磨损率(磨削比),而考虑到装夹工装及磨削机床的耦合影响,磨削力的变化也非常重要。尺寸精度和表面粗糙度是磨削工艺最重要的工艺目标,本例通过仿真研究对磨削砂轮选择、工艺参数变化等因素对表面粗糙度、材料去除率和砂轮磨损率(磨削比)影响均进行分析,并通过仿真研究给出定量结果。磨削力主要是顺磨削方向的切向力和与之垂直的径向力,这两个力与装夹方式及磨削主轴刚度有关,关系到磨削表面质量和磨削尺寸精度。精密磨削必须结合系统刚度对磨削力进行控制,否则出现因让刀形成的尺寸超差和磨削进入时磨削力冲击振动偶合形成振纹,导致表面粗糙度不合格,因此本文通过仿真分析对磨削力及磨削冲击力的数值进行定量研究,提出了成型磨削工艺参数与磨削加工性能、质量、经济性指标的定量化关系,对提高精密成型磨削加工技术及工艺水平有显著的意义。
文中砂轮线速度的取值范围为30~80 m/s,齿轮进给速度的取值范围为0~1 mm/s,砂轮的初始切深取30 µm。
2.2 表面粗糙度
由图5可知,表面粗糙度值随转速的增加而减小,随进给速度的增加而增加。这是因为,工件进给速度不变,则磨削表面固定,砂轮转速增加,则单位时间内磨粒与工件接触个数增加,因此表面粗糙度减小。砂轮转速不变,工件进给速度增加,单位时间内与工件接触的磨粒个数减少,表面粗糙度增加。
起初所做模型发现计算的表面粗糙度值过大,考虑为磨粒分布问题,故将磨粒按照整齐排列后再次运算,同一工况下运算前后的表面粗糙度值如图6所示,这说明砂轮表面砂粒分布对粗糙度有影响。
2.3 磨削力
本文忽略轴向力(在本文中当磨削余量均衡时这是内力),而采用F(径向力)与F(切向力)比值对磨削力进行分析。通过仿真导出砂轮不同方向受载荷的变化曲线(随步长、随行程),经过数据处理得出各工况下的F/F如图7所示。
F/F的时序图对设计砂轮磨削从进入磨削到满切过程的参数设计至关重要。从数值分析来看,稳定磨削阶段和进入阶段峰值力差了近三倍,并且性质上是冲击力。实践经验证明磨削大部分问题都是在这个阶段造成,但一般磨床在这个阶段是无控制的,磨削工艺也不管这个参数,在精密成型磨削中,仿真分析的研究必须要对其进行适合的工艺参数设计,削减其峰值负荷。
通过将磨削行程对应于模型上后,可得:在切入过程中,F/F<1;在即将进入满磨过程中,/在1左右;进入满磨后,F/F>1,且会基本稳定在固定数值上。
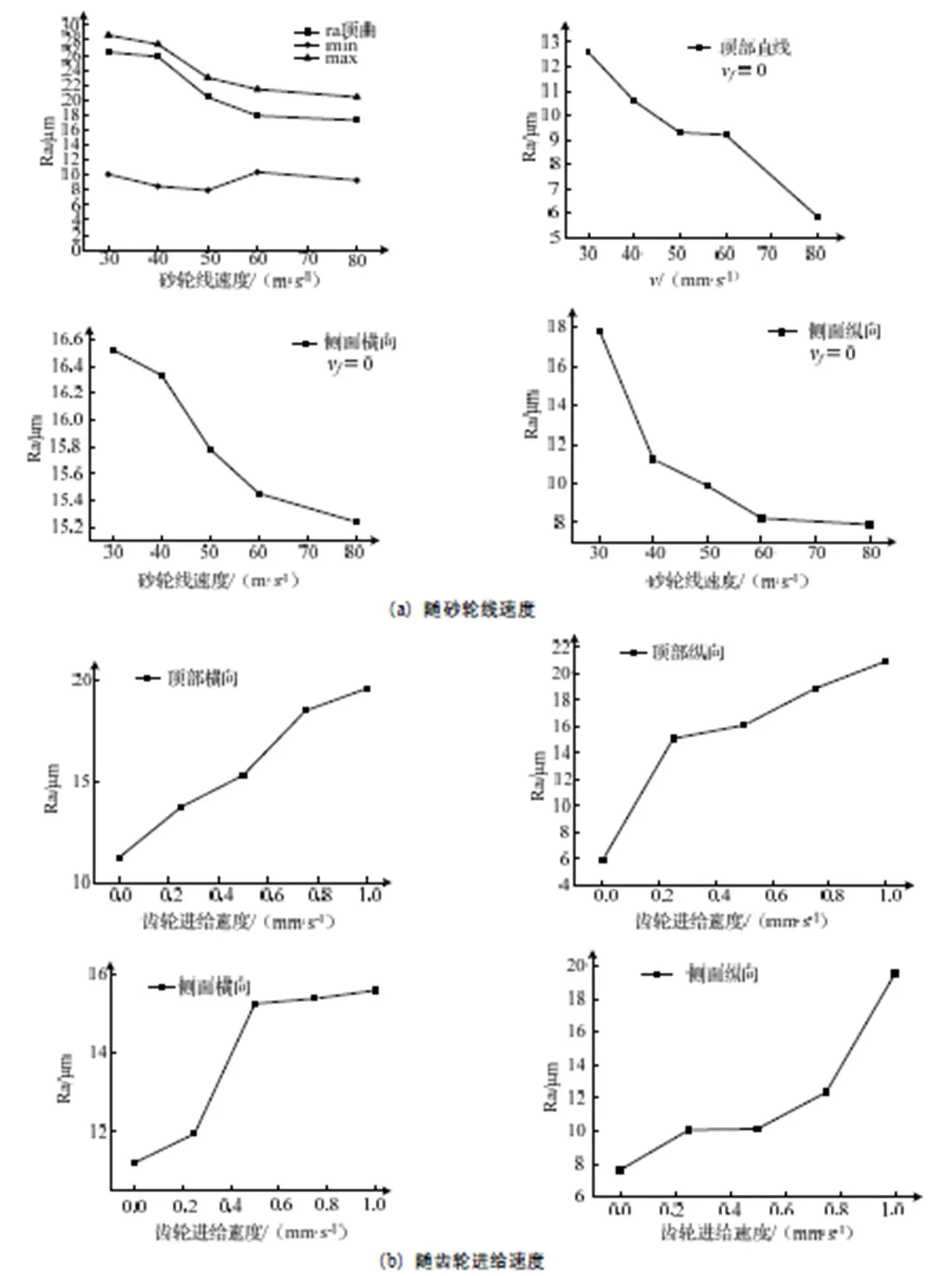
图5 表面粗糙度
与此同时,观察到F向数值较稳定、F向有突变点,判断可能是磨削造成材料迁移形成,借助软件将突变点追踪到模型(图8),发现F的突变点均出现在某处砂轮磨粒刚切入工件的瞬时,根据分析此处磨粒同别处磨粒区别即为突出高度过高,且处于曲面处,影响会更大。

图6 排列改变前后的表面粗糙度变化
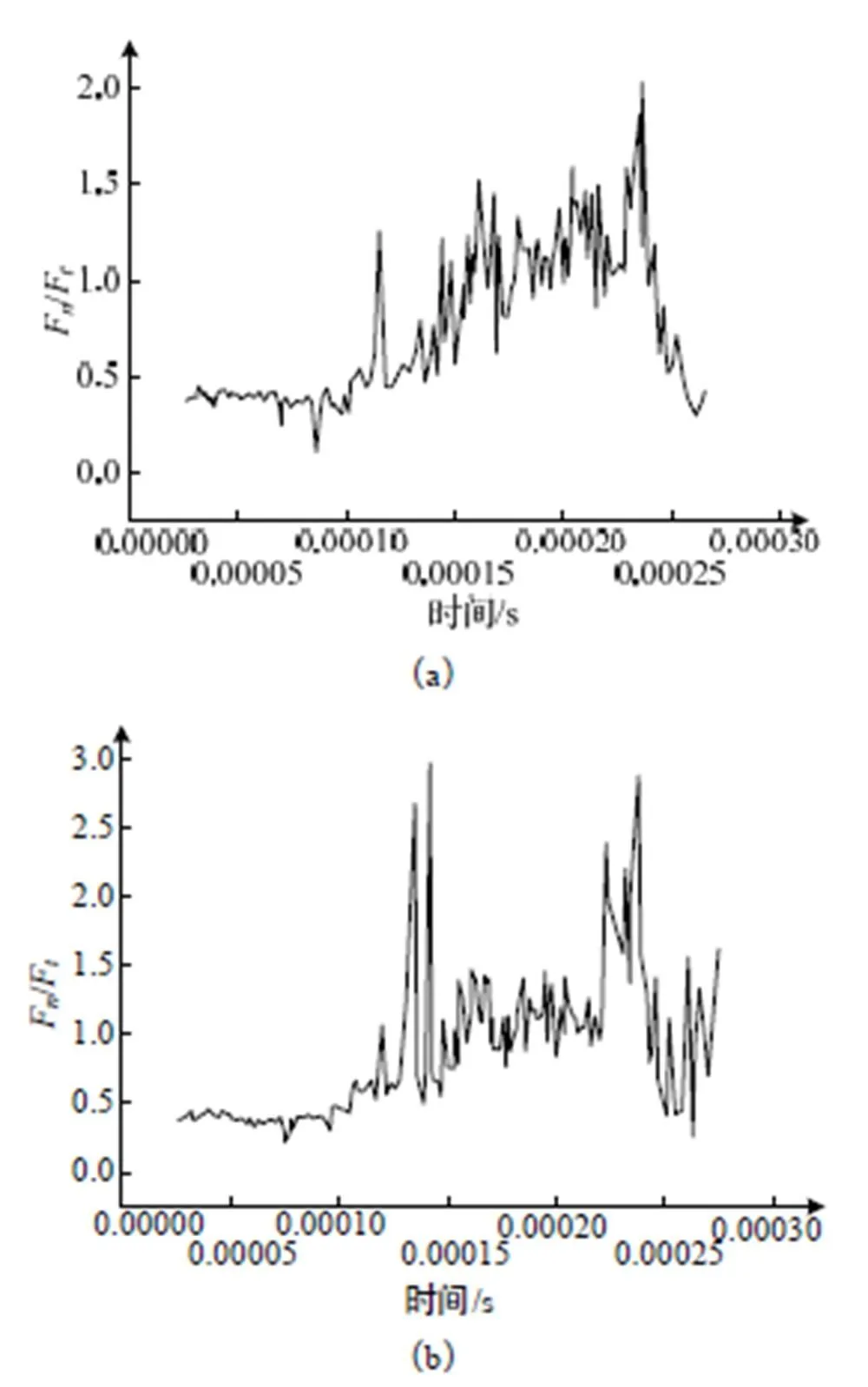
图7 Fn/Ft图
通过分析工件的每个节点受力情况,可以看到在进给方向存在反向的力,认为是物质迁移问题,故通过软件进行网格流动追踪如图9所示,箭头为受力矢量。研究分析普遍受力情况即可认为存在物质迁移塑性变形。可以看出,仿真研究的结论从侧面上也支持选用Usui的黏结模型是合理的。
2.4 材料去除率和砂轮磨损率
2.4.1 材料去除率
跟踪输出体积随磨削进程的变化情况,过数据处理得出材料去除量如图10所示,数据并非线性增长。表明砂轮完全进入达到满切状态时材料去除率进入稳定状态,符合实际情况。

图8 受力突变处运动位置

图9 网格流动追踪力矢量图示

图10 材料去除量
2.4.2 砂轮磨损量
根据等值线,统计计算求得一些点的砂轮磨损量。图11、图12分别按照齿轮进给速度不变、改变砂轮线速度,以及砂轮线速度不变、改变齿轮进给速度的变化情况进行了分析。
由于砂轮磨损量在初始阶段过小,并未达到软件可显示的数量级,且模型尺寸较小,故取点较少。研究可以看出,在进给速度、磨削深度不变的条件下,存在磨耗比最优的砂轮转速。图12中可以看出随着进给速度的增加,磨耗比存在波浪形起伏的变化,不能简单认为进给速度与砂轮磨耗比是线性的关系,这也说明精密磨削工艺优化的空间是比较大的。
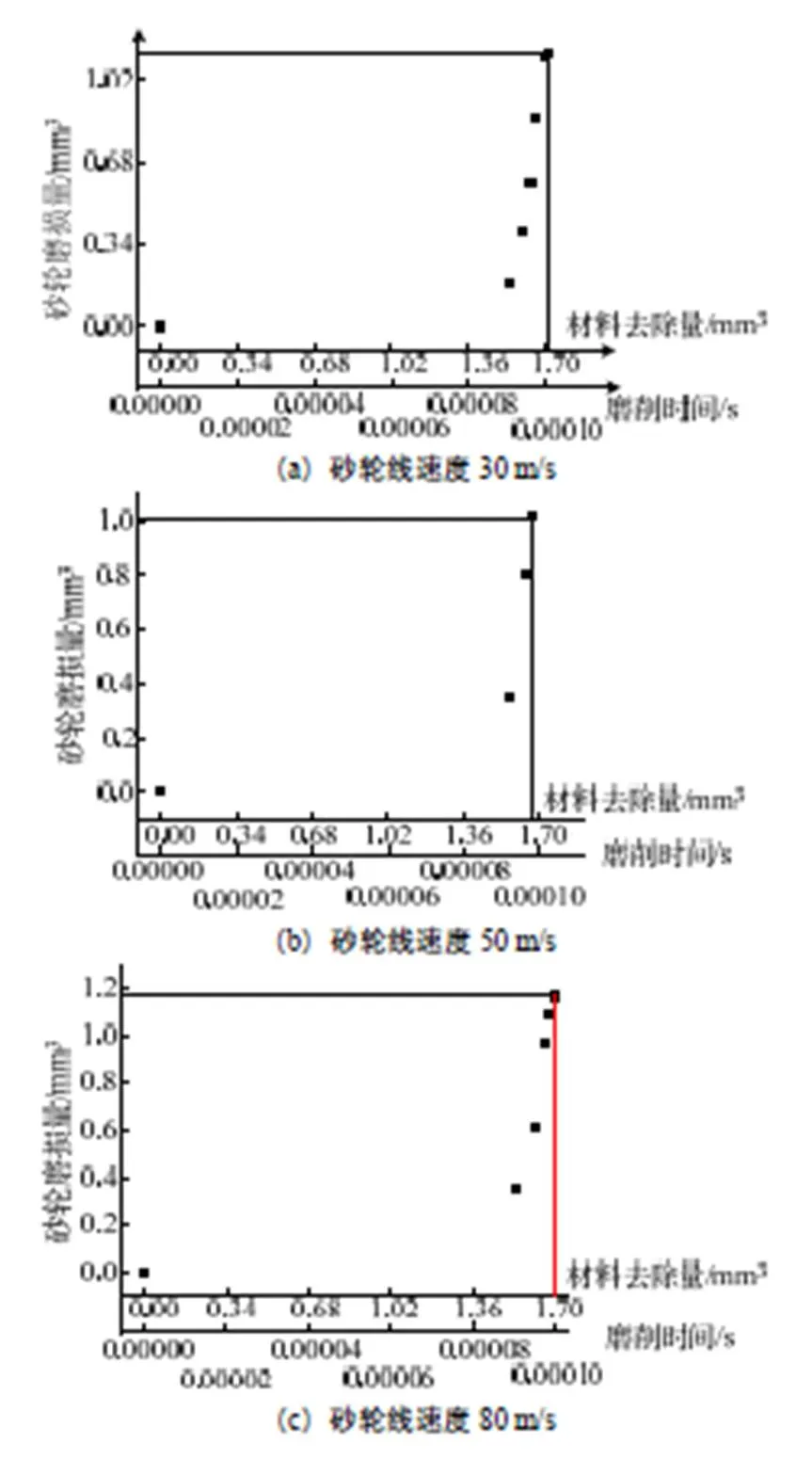
图11 改变砂轮线速度(摆线轮进给速度为1 mm/s)
2.5 二次走刀成型磨削的研究
成型磨工艺经常出现分二次或更多次数完成磨削,以每次磨削进给深度不变的条件进行研究。两次磨削深度均取0.03 mm,且在砂轮转速与摆线轮进给速度不变的情况下,研究表面粗糙度、材料去除率以及磨耗比的变化情况。
由于成型磨削砂轮母线并非直线,这意味着磨削各点的工艺参数有变化,这对工件磨削质量有影响,分别按照摆线轮的齿顶、齿侧部分(图13)进行了对比研究。同时,也对磨削方向对粗糙度的影响进行了探讨。

图12 改变齿轮进给速度(砂轮线速度80 m/s)
图13 摆线轮齿侧、齿顶示意图
可以看出,第二次磨削后,摆线齿轮齿顶以及齿侧的粗糙度都有降低,幅度大致20%~30%,这提示若要追求更低的粗糙度时可以在一定范围内考虑多次磨削工艺。对摆线齿轮来说,成型磨削要主要到齿侧的粗糙度要优于齿顶的粗糙度。
表面粗糙度较第一遍的变化情况如图14(a)所示,磨削第二次后的表面粗糙度均有所减小。砂轮磨损量和材料去除量的变化情况如图14(b)、(c)所示,二次磨削的材料去除量大于一次磨削,且砂轮磨损量随着磨削进程不断增加。
图14 二次磨削各参数变化情况
3 结论和建议
本次采用仿真软件为主要研究手段,对成型磨削仿真的建模技术、研究方法进行了系统性的技术研究,涉及到成型磨削工艺的主要工艺参数及其对磨削质量及磨削效率的影响,得出了定量结论,可以对改进及优化成型磨削工艺提出指导。并通过技术研究,得出了动态的F/F图,这实质上是成型磨削工艺参数对机床性能指标的要求。本研究得到以下结论:
(1)表面粗糙度值随转速的增加而减小,随进给速度的增加而增加。
(2)在进入成形磨满磨过程后,法向力峰值将会基本稳定在切向力峰值的三倍,且为冲击力。另,向的数值较稳定,向有突变点。
(3)随着进给速度的增加,磨耗比存在波浪形起伏的变化。
(4)二次磨削后,表面粗糙度有所减小,材料去除量增加,砂轮磨损量随磨削进程不断增加。
经过进一步发展完善,结合实际工艺参数的积累作必要的修正,仿真技术有望成为指导高精度成型磨加工的重要工具,对提高成型磨削的技术水平、提高精密零部件加工精度都有现实意义
[1]罗勇,陈蔚芳,陈奇伟,苏川. 大齿圈成形磨削仿真及余量分配技术研究[J]. 机械传动,2018,42(6):90-93.
[2]周涛. 合金渗碳钢20CrMnTi的成形磨削工艺试验及仿真研究[D]. 长沙:湖南大学,2012.
[3]杜晓阳. 成形磨齿加工仿真及误差分析[D]. 洛阳:河南科技大学,2011.
[4]张沭玥,周坤,王文健,郭俊,刘启跃. 打磨参数对钢轨打磨磨石磨损与材料去除影响研究[J]. 摩擦学学报,2018,38(3):327-333.
[5]Usui E,Kitagawa T,Shirakashi T. Analytical prediction of three dimensional cutting process -- Part 3: Cutting temperature and crater wear of carbide tool[J]. Journal of Engineer for Industry,1978,100(2):236-243.
Simulation Study on Simulation Precision Forming Grinding Process Parameters
LI Zhiwei1,ZHANG Shuyue2
( 1.Sichuan Machinery Research and Design Institute, Chengdu 610063, China; 2.Tribology Research Institute, Southwest Jiaotong University, Chengdu 610031, China)
In order to study the selection of process parameters in precision forming grinding, a three- dimensional model of cycloidal gear forming grinding is established by using CAD software. The corresponding simulation parameters are set up in DEFORM-3D finite element software. The effects of grinding wheel linear speed and cycloidal wheel feed speed on the surface roughness and grinding force after grinding are simulated and analyzed. The influence of material removal and wheel wear is also discussed. The results show that the surface roughness of the gear decreases with the increase of the linear velocity of the grinding wheel, increases with the increase of the feed velocity of the cycloid wheel, and decreases with the increase of the grinding times. After entering the full grinding process, the peak value of normal force will be basically stabilized at three times the peak value of tangential force. With the increase of feed speed, the variation of the grinding ratio is undulating.
forming grinding;material removal;surface roughness;grinding force;grinding ratio
TP391
A
10.3969/j.issn.1006-0316.2018.10.005
1006-0316 (2018) 10-0020-08
2018-09-10
李志伟(1971-),男,四川成都人,本科,副总工程师,主要研究方向为智能装备、机械传动、液压等。

