一系悬挂与扣件参数对钢轨波磨的影响分析

刘春阳，赵晓男，陈光雄，王科，崔晓璐



一系悬挂与扣件参数对钢轨波磨的影响分析

刘春阳，赵晓男，陈光雄，王科，崔晓璐

（西南交通大学 机械工程学院，四川 成都 610031）

基于摩擦自激振动可能导致钢轨波磨的观点，建立了更为完善的小半径曲线上轮轨系统摩擦自激振动模型，应用复特征值分析方法研究了轮轨系统的不稳定振动发生趋势，讨论了一系悬挂与轨道扣件刚度和阻尼参数对轮轨不稳定振动发生趋势的影响。计算结果表明：在饱和蠕滑力作用下，轮轨系统存在较强的不稳定振动发生趋势，即产生钢轨波磨的趋势；转向架一系悬挂刚度和阻尼参数对轮轨系统的自激振动影响较小；相对于一系悬挂，着重改善整体轨道上扣件的刚度和阻尼参数更有利于抑制钢轨波磨，且其中高轨上的扣件参数对钢轨波磨的影响起主要作用。

钢轨波磨；自激振动；一系悬挂参数；扣件刚度；扣件阻尼

钢轨波磨是在钢轨顶部表面形成的一种规律性的可见的类似波浪形状的周期不平顺磨损现象[1-2]。波磨的发展，不仅会带来环境噪音，还会引起车辆轨道结构的强烈振动，降低车辆和轨道结构部件的使用寿命，甚至导致行车事故[3]。目前，对于波磨还没有行之有效的根治方法，轻度的波磨通过打磨去除，严重的则只能通过更换新轨来控制[4]。但无论是哪种控制方式，其维护费用都异常昂贵。因此，研究钢轨波磨的形成机理和影响因素，从源头上消除波磨，具有极其重要的意义。

对于钢轨波磨的发生机理，金学松等[5]于2016综述了近40年来钢轨波磨的研究情况，将钢轨波磨的形成机理归纳为自激振动理论、反馈振动理论和其他理论。陈光雄[6-7]提出的当轮轨间的蠕滑力达到饱和状态，即蠕滑力等于轮轨间的法向接触力乘以动摩擦因数时，容易引发轮轨间的摩擦耦合自激振动导致钢轨波磨的观点可对目前地铁线路上的波磨的普遍现象做出较为合理的解释，且其预测波长和实际路线波长较为一致。本文基于该观点，建立了小半径曲线轨道上更为完善的轮轨系统模型，分别讨论了转向架一系悬挂参数和轨道支撑结构中单侧扣件参数对钢轨波磨的影响。

1 轮轨系统的摩擦自激振动模型

1.1 轮轨系统的接触模型

当车辆通过小半径曲线轨道时，车轮处于滚滑状态，车轮与钢轨间具有明显的相对滑移，导向轮对上外轮和内轮与钢轨间的蠕滑力均趋于饱和[8]，在饱和蠕滑力作用下，系统更容易发生摩擦自激振动，导致钢轨波磨。因此，本文主要研究导向轮对与钢轨间的摩擦自激振动情况。在普通短轨枕支撑的小半径曲线轨道上，地铁车辆导向轮对与钢轨间的接触模型如图1所示。左侧车轮与钢轨间的接触点位于车轮轮缘与钢轨轨头侧面之间，接触角为δ；右侧车轮与钢轨间的接触点位于车轮踏面和钢轨轨头之间，接触角为δ。转向架与轮对间一系悬挂横向刚度和阻尼分别为K和C，垂向刚度和阻尼分别为K和C。当车轮从轨道上滚过时，轮轨间分别产生了法向接触力N和N及蠕滑力F和F。扣件垂向刚度和阻尼分别为K和C，扣件横向刚度和阻尼分别为K和C。轨枕垂向支撑刚度和阻尼分别为K和C，横向支撑刚度和阻尼分别为K和C。

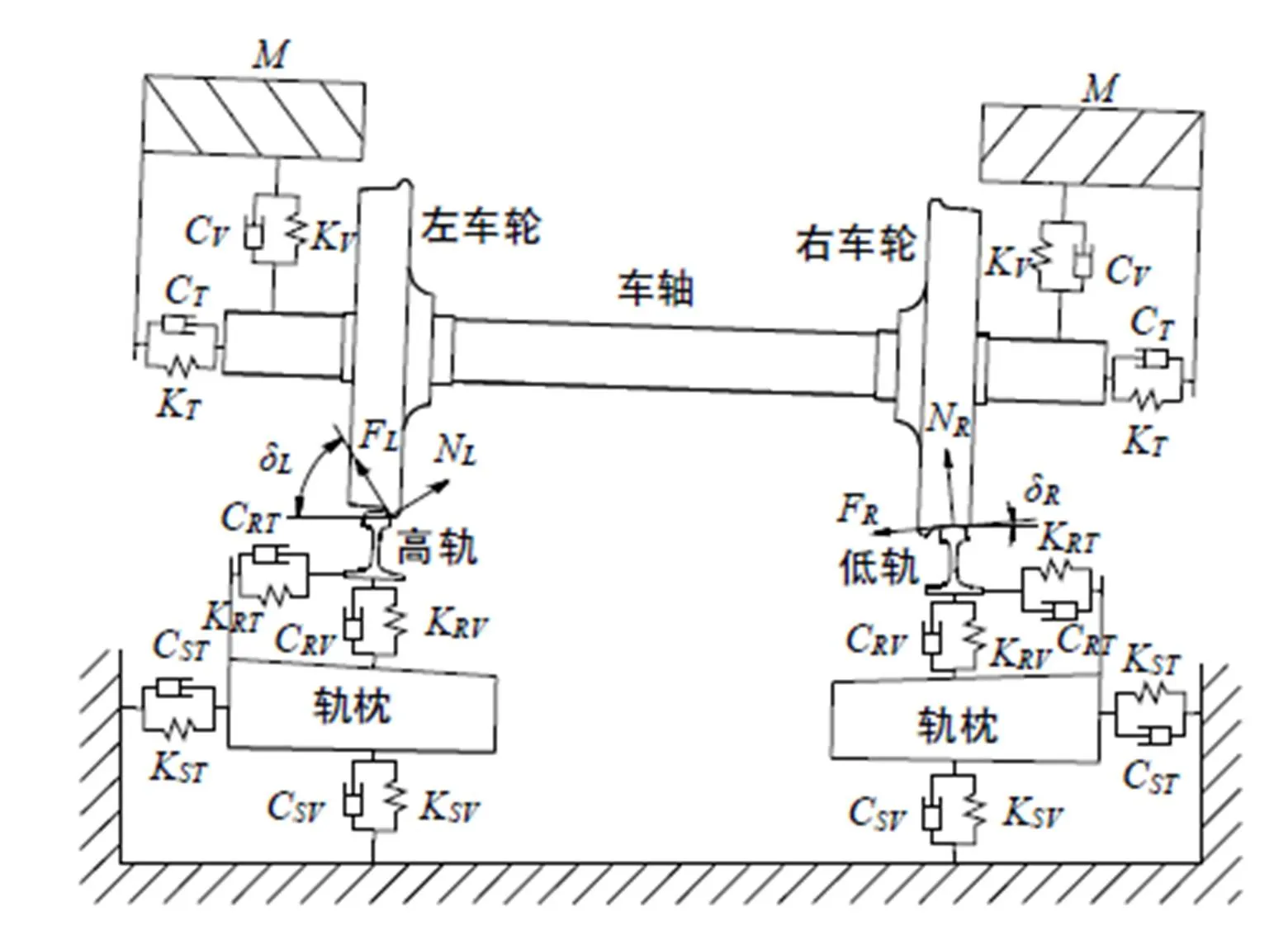
图1 小半径曲线轨道上轮轨系统接触模型

1.2 轮轨系统的有限元模型

根据如图1，结合轮轨的实际几何参数，利用Abaqus建立了普通短轨枕支撑小半径曲线轨道上导向轮对－钢轨系统的摩擦自激振动有限元模型，如图2所示。轨道长36 m，钢轨为60 kg/m的标准钢轨，轨距＝1435mm，轨底坡为1/40，两端采用固定约束。车轮直径840 mm，踏面为LM型磨耗型踏面。在轨道支撑结构中，钢轨和轨枕之间采用DTVI2扣件连接，前后扣件的间距＝625 mm，扣件系统通过平行的点对点的弹簧和阻尼单元模拟，垂向支撑刚度和阻尼分别为K＝40.73 MN/m，C＝9898.70 Ns/m，横向支撑刚度和阻尼为K＝8.79 MN/m，C＝1927.96 Ns/m。由于普通短轨枕支撑直接嵌入在轨道板内，忽略道床对轨枕的支撑刚度和阻尼，普通短轨枕支撑和道床的整体支撑刚度和阻尼采用接地弹簧和阻尼单元模拟，其垂向支撑刚度和阻尼分别设置为K＝89 MN/m和C＝89800 Ns/m，横向支撑刚度和阻尼分别设置为K＝50 MN/m和C＝40000 Ns/m[9]。转向架一系悬挂垂向刚度和阻尼分别为K＝1260 kN/m和C＝10626 Ns/m，一系悬挂横向刚度和阻尼分别为K＝6500 kN/m和C＝80650 Ns/m，纵向刚度和阻尼分别为K＝10000 kN/m和C＝98200 Ns/m。车体、乘客和转向架构架等簧上质量用质量块单元模拟，并通过一系悬挂弹簧和阻尼单元连接到车轴。弹簧和阻尼单元如图2所示。模型采用C3D8I六面体单元划分网格，总单元数为270300，钢轨和车轮间的摩擦因数为0.45，钢轨和轮对的弹性模量均为＝2.17×1011N/m2，密度＝7.8×103kg/m3，泊松比＝0.3。轨枕的弹性模量＝1.9×1011N/m2，密度＝7.8×103kg/m3，泊松比＝0.3。

图2 轮轨系统有限元模型

1.3 轮轨系统运动方程

本文采用复特征值分析方法在频域上研究了轮轨系统的有限元模型发生摩擦自激振动的趋势。在分析中，轮轨系统摩擦自激振动方程[10]为：

式中：为系统节点位移矢量；、和分别为轮轨系统的质量、阻尼和刚度矩阵，由于摩擦力耦合作用，、和均为非对称矩阵。

由于当轮对的蠕滑力达到饱和状态时，轮轨系统将出现不稳定，这时的复特征值会出现负数。故可得到式（1）的通解：

式中：β和ω分别代表该特征值的实部和虚部；φ为特征向量；λ＝β＋ω为第阶复特征值。

当复特征值出现正实部，即β＞0时，轮轨系统在此特征值对应的频率下可能会发生摩擦自激振动。等效阻尼比ξ＝-2β/(π|ω|)也是判断自激振动发生趋势的重要参数[11]：当等效阻尼为负数时表明系统此时可能会发生不稳定振动，且绝对值越大，其发生趋势也就越大。

2 计算结果与分析

2.1 轮轨系统摩擦自激振动的模态分析

本文采用复特征值分析法对轮轨系统进行稳定性分析，预测得到轮轨系统的不稳定振动频率以及相应的振动模态。图3是轮轨系统在频率范围为0～1200 Hz的负等效阻尼比分布情况，可看出，此时结果中存在两个负的等效阻尼比，分别为-0.03064和-0.00740，对应的频率分别为498.12 Hz和514.65 Hz，这说明轮轨系统存在两个不稳定振动频率，对应的不稳定振动模态如图4所示，可以发现其不稳定振动主要发生在轮轨系统的内侧车轮和低轨上。由于等效阻尼比绝对值越大，相应的自激振动越容易发生。因此认为最小等效阻尼比＝-0.03064时，轮轨系统的摩擦自激振动最容易发生，对应的不稳定振动频率为498.12 Hz。

图3 小半径曲线轨道上轮轨系统摩擦自激振动频率分布图

2.2 一系悬挂参数对钢轨波磨的影响

现有文献中考虑转向架对钢轨波磨影响的研究很少。本文通过仿真分析研究了转向架一系悬挂刚度和阻尼参数对钢轨波磨发生趋势的影响。

为研究一系悬挂刚度对钢轨波磨的影响，本节在其他模型参数不改变的情况下，仅分别调整一系悬挂的相应刚度为原来的2、1.6、1.4、1、0.8、0.6、0.4等相关倍数，这里须指出，选取相关原模型参数的一定倍数来进行计算，只是为了寻找该参数对钢轨波磨的影响规律。图5给出了随着一系悬挂刚度的调整，不稳定振动所发生的变化情况。从图5（a）中可以发现，轮轨系统的不稳定振动没有随着一系悬挂刚度的改变而在个数和频率上发生变化，其两个不稳定频率均在498.12 Hz和514.65 Hz左右，这说明一系悬挂刚度对波磨的频率基本不产生影响。从图5（b）中可以发现随着一系悬挂刚度的调整，不稳定振动的等效阻尼比变化幅度很小。综合计算结果，本文认为转向架一系悬挂刚度参数的大小对钢轨波磨的影响很小。

本文研究了转向架一系悬挂的垂向阻尼参数对钢轨波磨的影响。如上节一样，在其他模型参数不改变的情况下，仅调整垂向阻尼C为原参数的相关倍数，分别对轮轨系统振动模型进行了计算，其结果如图6所示。在图6（a）中可以发现，随着一系悬挂垂向阻尼C的调整，不稳定振动频率的个数并没有出现变化，但随着垂向阻尼C的增大，不稳定振动的频率出现单调的轻微降低现象。图6（b）中可以发现，两个不稳定振动对应的等效阻尼比均呈现了随一系悬挂垂向阻尼C增加而增大、但曲线的变化趋势相对较小的现象。因此，结合计算结果，本文认为一系悬挂的垂向阻尼C对钢轨波磨的影响较小，从而增大或者减小一系悬挂的垂向阻尼C并不能达到显著抑制钢轨波磨的目的。

图5 一系悬挂刚度对钢轨波磨的影响

图6 一系悬挂阻尼对钢轨波磨的影响

2.3 扣件参数对钢轨波磨的影响

等效阻尼比的绝对值越大，摩擦自激振动发生的概率就越大，图7列出了系统自激振动的主要等效阻尼比随扣件刚度调整而出现的变化。在图7（a）中，随着整体扣件横向和垂向刚度的增大，系统的等效阻尼比绝对值呈明显减小趋势，说明在一定范围内，增大整体扣件的刚度可以有效的抑制钢轨波磨。在图7（b）中，当高轨扣件刚度不变，仅增大低轨扣件刚度时，轮轨系统的等效阻尼比的变化很小，低轨扣件刚度对钢轨波磨的影响较小。图7（c）可以发现，低轨刚度不变，随着高轨轨道扣件横向和垂向刚度的增大，系统的等效阻尼比绝对值有明显减小的趋势，且其趋势与图7（a）大致相同，这说明高轨上的扣件刚度对钢轨波磨发生趋势影响较大。

图7 扣件刚度对钢轨波磨的影响

综合以上分析，本文认为在一定范围内增大整体轨道上的扣件刚度有助于改善波磨产生，且高轨上的扣件刚度对抑制波磨起到主要作用。

扣件阻尼参数对钢轨波磨的影响情况如图8所示。从图8（a）和（c）可看出，随着整体轨道和高轨上扣件参数在一定范围内按比例的增大，轮轨系统不稳定振动的等效阻尼比绝对值有明显增大趋势；而在图8（b）中，当仅增大低轨扣件的阻尼参数时，不稳定振动的等效阻尼比的变化趋势却很小。结合摩擦自激振动导致钢轨波磨的观点，本文认为在一定范围内减小高轨上或整体轨道上的扣件阻尼参数可以有效缓解钢轨波磨，而仅改变低轨上的扣件的阻尼参数并不能起到缓解钢轨波磨的作用。

图8 扣件刚度对钢轨波磨的影响

3 结论

（1）当地铁车辆通过小半径曲线轨道，转向架前轮对轮轨间的蠕滑力达到饱和时，轮轨系统易发生摩擦自激振动，导致主要发生频率在500 Hz左右，存在于低轨上的钢轨波磨。

（2）车辆转向架一系悬挂刚度和阻尼参数对钢轨波磨影响较小，并不能通过调整转向架的一系悬挂参数来达到抑制钢轨波磨的目的。

（3）在轨道支撑结构中，通过调整整体扣件刚度或阻尼都可以有效缓解钢轨波磨，且其中高轨上的扣件参数起到了主要作用，仅改变低轨上的参数并不能降低钢轨波磨发生趋势。

[1]钱韦吉. 铁路轮轨和弓网系统摩擦自激振动瞬态动力学研究[D]. 成都：西南交通大学，2014.

[2]温泽峰. 钢轨波浪形磨损研究[D]. 成都：西南交通大学，2006.

[3]CUI X L，CHEN G X，YANG H G，et al. Effect of the wheel/rail contact angle and the direction of the saturated creep force on rail corrugation. Wear，2015（330-331）：554-562.

[4]SINGLETON R，MARSHALL M B，LEWIS R，et al. Rail grinding for the 21st century–taking a lead from the aerospace industry [J]. Proceedings of the Institution of Mechanical Engineers，Part F: Journal of Rail and Rapid Transit，2014，229（5）：457-65.

[5]金学松，李霞，李伟，等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报，2016，51（2）：264-273.

[6]陈光雄，钱伟吉，莫继良，等. 轮轨摩擦自激振动引起小半径曲线钢轨波磨的瞬态动力学研究[J]. 机械工程学报，2014，50（9）：72-76.

[7]CHEN G X，ZHOU Z R，OUYANG H，et al. A finite element study on rail corrugation due to saturated creep force-induced self-excited vibration of a wheel-rail system [J]. Journal of Sound and Vibration，2010，3294：643-6455.

[8]SUN Y Q，SIMSON S. Nonlinear three -dimensional wagon-track model for the investigation of rail corrugation initiation on curved track [J]. Vehicle System Dynamic，2007，45（2）：113-132.

[9]LI W，Wang H Y，WEN Z F，et al. An investigation into the mechanism of metro rail corrugation using experimental and theoretical methods [J]. Proceedings of the Institute of Mechanical Engineers Part F-Journal of Rail and Rapid Transit，2015：0954409715596182.

[10]OUYANG H. Numerical analysis of automotive disc brake squeal: a review [J]. International Journal of Vehicle Noise and Vibration，2005，1（3/4）：207-231.

[11]YUAN Y. An eigenvalue analysis approach to brake squeal problem[C]. Proceedings of the 29th ISATA Conference Automotive Braking Systems，Florence，Italy，1996：337-344.

Influence of Primary Suspension and Rail Fastener Parameters on Rail Corrugation

LIU Chunyang，ZHAO Xiaonan，CHEN Guangxiong，WANG Ke，CUI Xiaolu

( School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China )

The friction-induced self-excited vibration may lead to rail corrugation. In order to understand its influence, an improved friction-induced self-excited vibration model for wheel-rail system on a sharp curved track of a metro line has been adopted to study the trend of the unstable vibration of the wheel-rail system with complex eigenvalue analysis method, on the one hand, and to discuss the influence of stiffness and damping of the primary suspension and fastener on the occurrence propensity of the friction-induced self-excited vibration, on the other hand. The simulation results show that the unstable vibration of wheel-rail system is more easily to occur under the effect of the saturated creep force, which leads to rail corrugation. The damping and stiffness parameters have a little influence on self-excited vibration of wheel-rail system. Improving the stiffness and damping parameters of the integral track fastener is more conducive to the suppression of rail corrugation, and the fastener parameters of the high rail have a major influence on rail corrugation.

rail corrugation；self-excited vibration；parameters of primary suspension mechain；fastener stiffness；fastener damping

TH117；U211

A

10.3969/j.issn.1006-0316.2018.10.003

1006－0316 (2018) 10－0011－06

2018－01－09

国家自然科学资金项目（51775461）

刘春阳（1991－），男，吉林榆树人，硕士研究生，主要研究方向为轮轨振动振动与噪声。