超精细结构效应对辐射光谱圆极化特性的影响∗

陈展斌 董晨钟

1)(西北师范大学物理与电子工程学院,兰州 730070)

2)(湖南工业大学理学院,株洲 412007)

3)(国防科学技术大学理学院,长沙 410073)

(2018年2月10日收到；2018年7月19日收到修改稿)

1 引 言

近些年来,高分辨率和高灵敏度的激光光谱技术的发展为人们探究超精细结构开启了一个崭新的窗口,使得一些复杂原子的超精细结构以及相关效应的研究成为可能.例如,同位素位移效应[1]、核自旋引起的超精细猝灭效应[2]以及宇称不守恒效应[3]等.考虑到超精细结构效应后,原子体系的角动量F将由电子的总角动量J和原子核的角动量I耦合而成,即F=I+J.不同于精细结构情况下的总角动量J,此时原子体系能级之间的跃迁选择定则由体系总角动量F描述.这将导致在某些情况下,在精细结构层次上选择定则禁戒的跃迁也可能发生.实验上,Wada等[4]通过对7Be+超精细光谱的高精度测量,确定了7Be+核的磁偶极矩.Brandau等[5]在储存环上利用电子与高离化态离子碰撞的方法测定了Nd57+的同位素偏移,进而得到了相应的原子核半径.Trotsenko等[6]在类锂U89+离子双激发态的实验中发现,一些禁戒跃迁的概率随着原子序数增大,甚至变为主要的退激发通道.理论方面,Yu等[7]利用相对论多体理论计算了43Ca+和87Sr+中的超精细结构常数,并探讨了极化效应和关联效应的影响.Sahoo[8]利用相对论耦合簇理论计算得到了高精度Ba+离子5d2D3/2态和5d2D5/2态的超精细结构常数,并分析了核极化效应的影响.Cheng等[9]利用相对论多组态模型计算了类铍离子(Z=6—92)超精细诱导2s2p3P0→2s21S0的跃迁概率,并与实验测量进行了比较.其他有关报道见文献[10—14].

考虑原子核的性质后,电子、光子和离子等粒子与高离化态原子的碰撞动力学过程也将受到影响.例如,Zolotorev和Budkes[15]讨论了在储存环上开展研究宇称不守恒实验研究的可行性.Henderson等[16]通过测量类氦Sc19+离子退激发辐射X射线的线性极化度,发现超精细结构效应极大地影响了谱线的极化特性.Gumberidze等[17]测量了裸铀离子在辐射复合过程辐射的X射线光谱,并确定了类氢U91+离子基态的Lamb位移.James等[18]从实验上测量了电子碰撞激发氢原子的截面以及退激发光谱的线性极化度,并利用经验公式进行了拟合.Dubau等[19]利用相对论扭曲波方法估算了超精细结构效应对类氦Sc19+退辐射X射线的线性极化度的影响,发现超精细结构相互作用具有较强的去极效应.

事实上,电子与高离化态离子碰撞激发中辐射跃迁光谱极化和角向特性的研究,为人们探究强库仑场中各种物理效应提供了重要的路径[20−22].我们之前也已开展过一些研究工作[23−30],然而就我们所知,目前电子碰撞激发的研究大部分集中在精细结构层次,超精细结构层次上的研究工作较少.此外,由于大部分研究采取非极化电子入射,有关退激辐射过程的报道只涉及光谱的线性极化特性.例如,Bensaid等[22]研究了非极化电子碰撞激发类氦205Tl79+离子1s21S0→1s2p3P2过程以及退激发过程中E1-M2干涉效应对光谱线性极化度的影响.由极化电子与高离化态离子碰撞引起的辐射光谱圆极化度的研究非常匮乏.

本文在相对论多组态Dirac-Fock方法和密度矩阵理论的基础上,利用发展的处理纵向极化电子碰撞激发的程序,系统研究了超精细结构效应对纵向极化电子碰撞激发过程以及退激发辐射光谱圆极化特性的影响.计算了纵向极化电子碰撞激发类氦Sc19+和205Tl79+离子1s21S0→1s2p3P2精细结构层次上的碰撞强度,进而转化得到了超精细结构层次上MF能级的碰撞强度,并在超精细结构层次上考察了辐射衰变过程中发出特征光子的极化特性.随后,分析了E1-M2量子干涉效应对相关谱线极化特性的贡献,并研究了电子-电子间相互作用的相对论修正(即Breit相互作用)对碰撞激发过程及退激发辐射光子极化特性的影响.

2 理论模型

考虑到处于激发态的原子发生辐射跃迁,从较高的∆iJiMi态到低的∆fJfMf态,其中∆表示惟一描述激发态所需的除JM之外的量子数,由密度矩阵理论可知,原子系统与电磁场的相互作用势V的跃迁矩阵元∆iJiMi→∆fJfMf可以展开成电和磁多极组分,表示为[22]

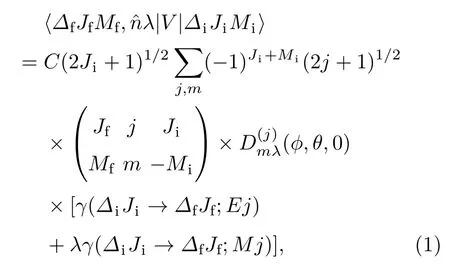
ω为发射光子的能量,Λ(π)取值0和1,分别表示电和磁多极. ⟨∆fJf||Q(jπ)||∆iJi⟩为多极矩算符Q(jπ)下的矩阵元.跃迁概率表示为

自然地,所有满足选择定则的跃迁都包含在(1)式中.

光子的密度矩阵可以写为[22]

式中,纯的电偶极(E1)跃迁和磁四极(M2)跃迁以及干涉项的贡献都清楚地分离开来.进一步,极化参量可以表示为[22]

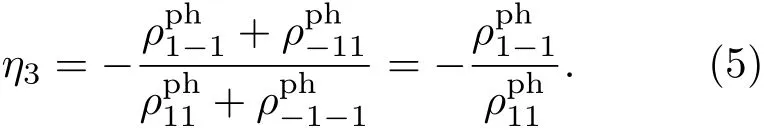
限于篇幅,具体表达式见文献[22].超精细结构层次上,需将超精细结构能级上占据数NMF替换NMi.转化公式为

式中,I为核自旋,F为系统总角动量,ΩMJ为精细结构层次上磁量子数M的激发强度.

在目前的计算中,我们使用发展的全相对论扭曲波程序来计算精细结构层次上纵向极化电子碰撞激发截面及相关的辐射线圆极化特性,相关理论及计算流程在文献[23—30]中已有介绍.相对论散射矩阵元如下

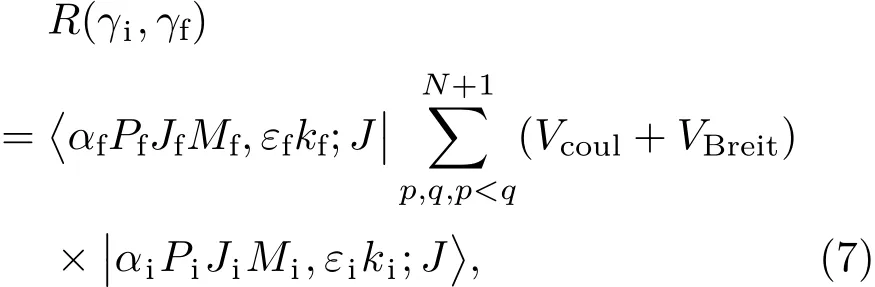
式中,碰撞体系初、末态反对称化的波函数分别为|αiPiJiMi,εiki；J⟩和 ⟨αfPfJfMf,εfkf；J|,Vcoul表示Coulomb算符,具体形式如下:

rqp表示任意两个单电子间的距离；VBreit表示Breit相互作用算符,具体形式如下:

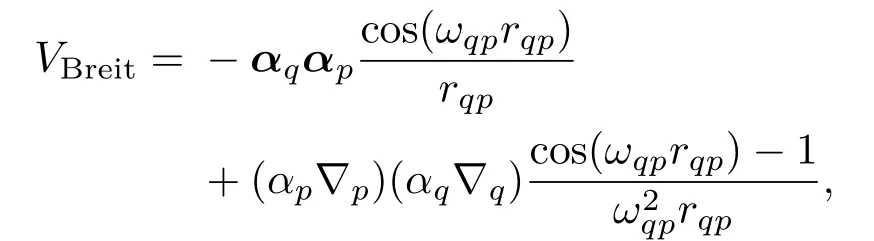
3 结果与讨论

在前期工作的基础上[23−30],我们进一步编写了相应的代码拓展到超精细结构层次.其中,靶态离子波函数的计算由相对论原子结构程序包GRASP92得到,连续电子波函数由RATIP程序包的子程序COWF计算得到.在电子碰撞激发截面的计算中,为了保证计算的收敛,我们取最大分波数κ=90.在目前的工作中,我们考虑了高离化态类氦Sc19+离子和205Tl79+离子,选择这两个离子作为研究对象的原因在于:1)Sc19+离子具有较大的核自旋(I=7/2),由于原子序数较低,一些高阶效应相对较小,因而可以较容易地反映超精细结构效应的影响；2)相比于Sc19+离子,205Tl79+离子具有较大的原子序数和较小的核自旋(I=1/2),相对论效应,量子电动力学效应等显著,为我们分析和探讨高阶物理效应提供了条件；3)早期已有相关实验测量了其电子碰撞激发过程及退激发辐射光谱的极化特性,便于比较,同时也能对我们发展的计算程序进行检验.

3.1 辐射跃迁分支比

表1给出了高离化态类氦Sc19+离子和205Tl79+离子在1s2p3P2→1s21S0超精细结构层次上不同F能级退激到基态的电偶极E1跃迁概率以及电偶极E1和磁四极M2跃迁的分支比,同时与文献[22]中的结果进行了比较.注意到,由于还存在着其他高阶的跃迁,因而表中各F能级电偶极E1和磁四极M2分支比之和并不等于1.我们的计算与早期文献中的结果符合得非常好.对于Sc19+离子,核自旋I=7/2,与电子总角动量J=2耦合后将出现5个F能级.对于205Tl79+离子,核自旋I=1/2,耦合后将出现两个F能级.从表1中可以看到,除占主导的磁四极M2跃迁概率显著大于电偶极E1跃迁外,不同F能级到基态的跃迁并不呈现明显的规律性.对于Sc19+离子,Ff=7/2→Fi=5/2能级之间的跃迁纯磁四极与纯电偶极RM2/RE1的比率为2.673,而Ff=7/2→Fi=7/2能级之间的跃迁纯磁四极与纯电偶极RM2/RE1的比率为1.502.

表2和表3分别给出了纵向极化电子在不同入射能量下与高离化态类氦Sc19+离子和205Tl79+离子1s21S0→1s2p3P2的碰撞激发强度.计算中我们忽略了超精细结构效应对靶态结构的影响,同时散射矩阵元中没有考虑Breit相互作用的贡献.从表2可以看到,对于氦Sc19+离子的激发过程,在较低的入射能量下,磁量子能级Mf=1的碰撞强度最大,Mf=−2的最小,随着入射能量的增大,各磁量子能级强度逐渐减小.205Tl79+离子的计算结果与Sc19+离子的情况类似,呈现出相同的变化规律.

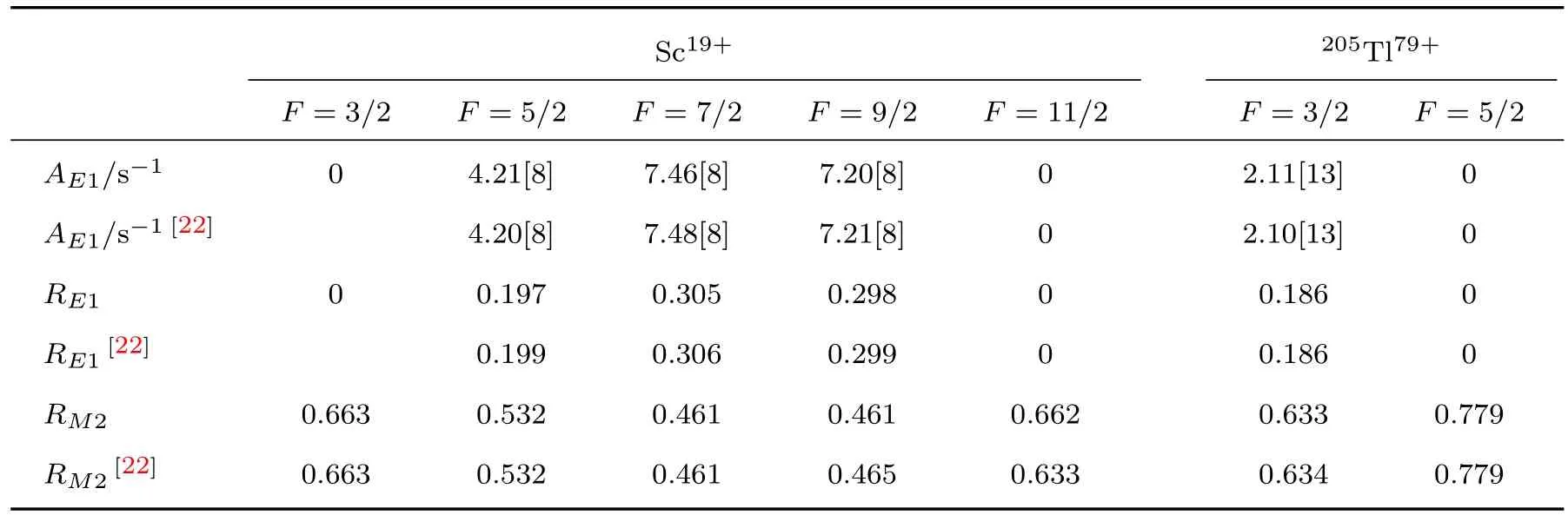
表1 类氦Sc19+离子和205Tl79+离子1s2p3P2→1s2 1S0不同超精细组分能级E1跃迁概率以及E1和M2跃迁的分支比 (a[b]=a×10b)Table 1.Branching ratios RE1and RM2for the E1 and M2 decay channels occurring in each hyper fine component 1s2p3P2→1s2 1S0for both ions Sc19+and205Tl79+.The calculated transition probabilities AE1from the different F-sublevels are also given(a[b]means a×10b).

表2 纵向极化电子碰撞激发类氦Sc19+离子1s2 1S0→ 1s2p3P2在不同磁子能级碰撞强度(X为阈值能量单位)(a[b]=a×10b)Table 2.Calculated collision strengths for longitudinally-polarized EIE of He-like Sc19+ions from the ground level 1s2 1S0to each magnetic sublevels of the 1s2p3P2level(X is the threshold energy unit)(a[b]means a×10b).

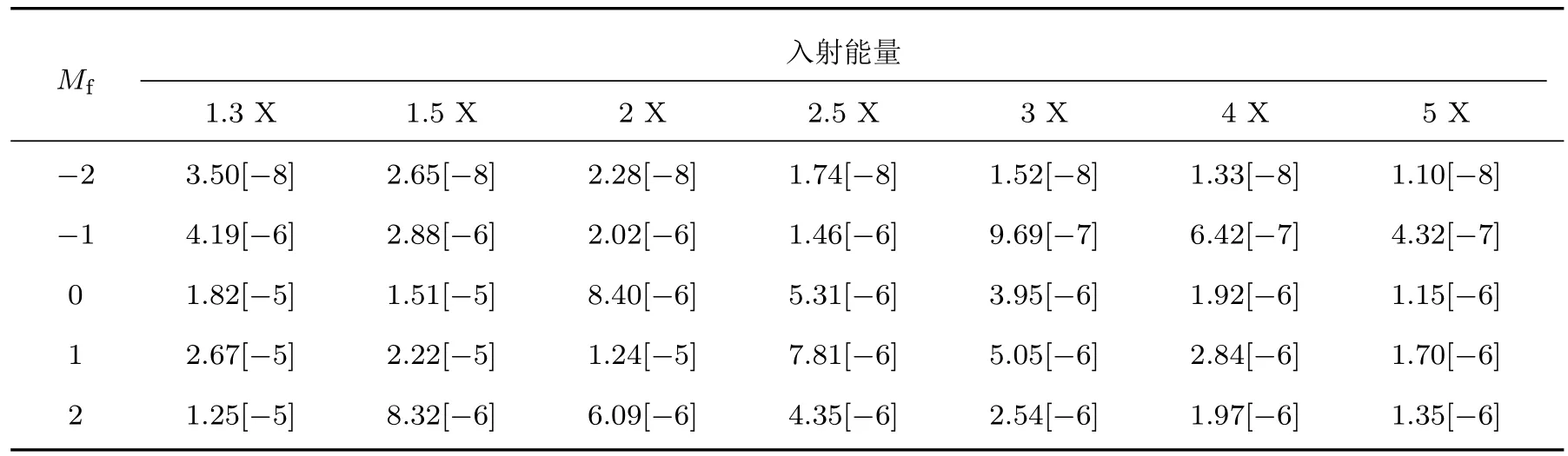
表3 纵向极化电子碰撞激发类氦205Tl79+离子1s2 1S0→ 1s2p3P2在不同磁子能级碰撞强度(X为阈值能量单位)(a[b]=a×10b)Table 3.Calculated collision strengths for longitudinally-polarized EIE of He-like205Tl79+ions from the ground level 1s2 1S0to each magnetic sublevels of the 1s2p3P2level(X is the threshold energy unit)(a[b]means a×10b).

利用表2和表3,我们进一步将磁量子能级|Mf|上的碰撞强度转化到超精细能级|MF|上,转化的的结果分别列在表4和表5中(X为阈值能量单位).不难发现,在不同能量情况下,从基态激发到超精细能级MF的强度并不相同,随着能量的增大,超精细能级MF的强度逐渐减小.此外,由同一角动量F不同超精细MF能级之间转化的碰撞强度也不一样.例如,对于类氦Sc19+离子的碰撞激发过程,角动量F=11/2,MF=11/2,7/2,5/2,3/2能级的碰撞强度较大,而MF=−11/2上的碰撞强度为0.对于角动量F=9/2,MF=9/2,7/2,5/2能级的碰撞强度较大,MF=−7/2能级的碰撞强度最小.这说明,碰撞激发过程中,纵向极化电子在超精细能级层次上的布局情况并不相同,可以发现,对于给定的角动量F,纵向极化电子优先占据MF较大的几个能级上,而在MF较小能级的占据相对较小.其原因在于电子的方向性导致了这些激发的离子成行排列,引起了不同能级的优先集居.

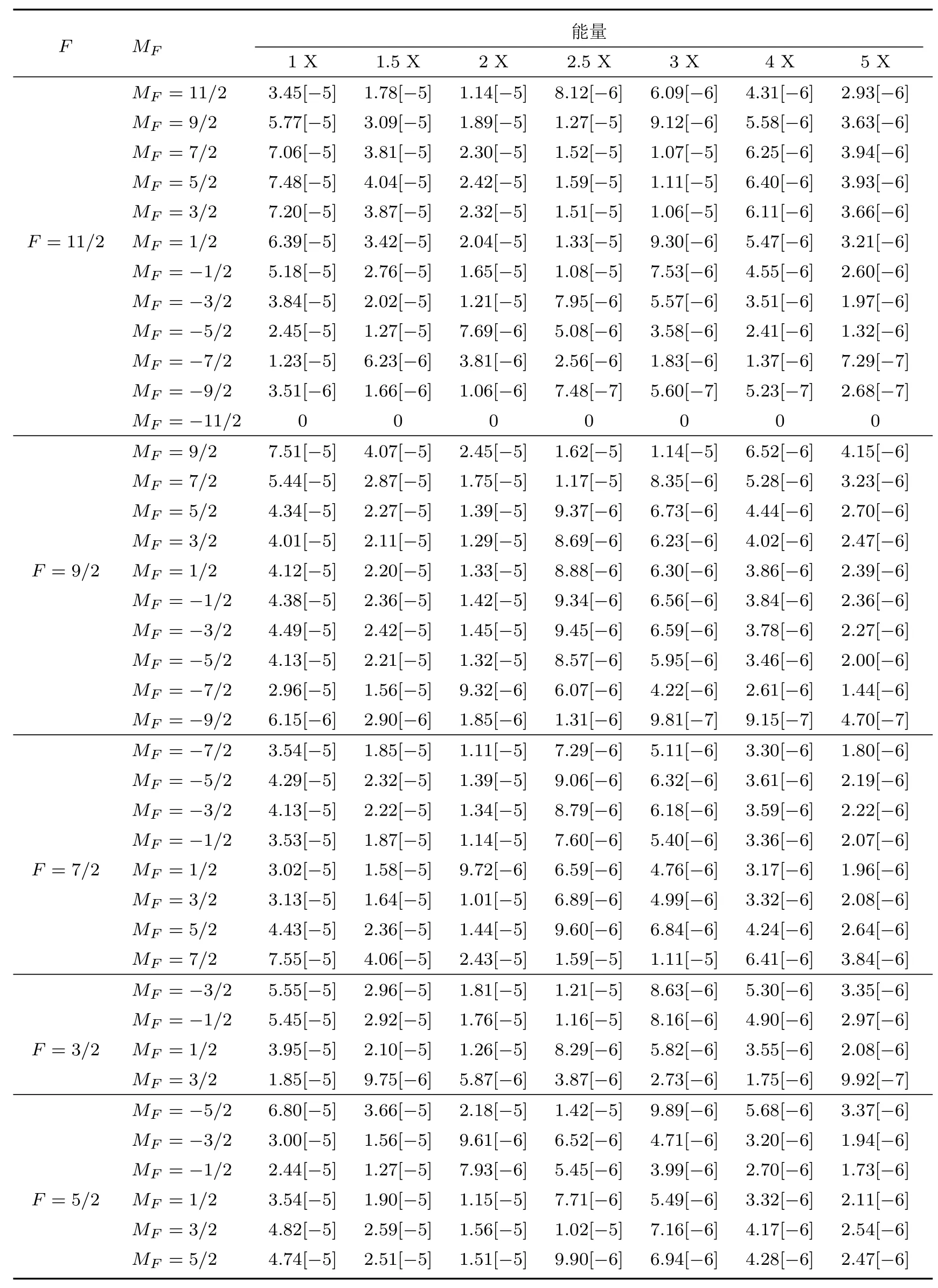
表4 与表2类似,但是对于MF超精细能级Table 4.The same as in table 2,but for the different MFof hyperfine sublevels.

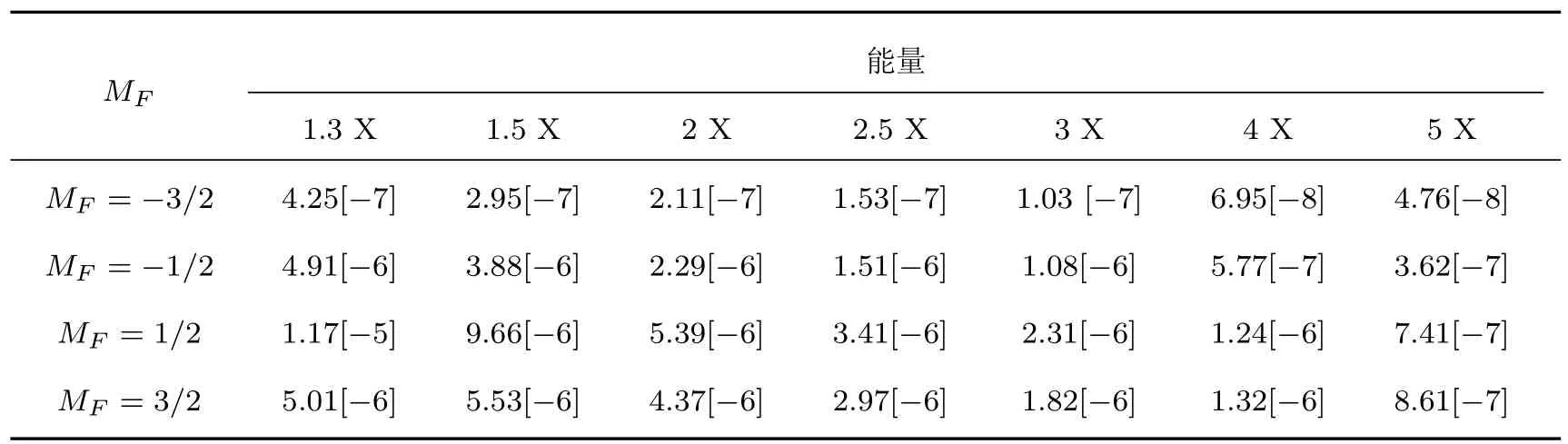
表5 与表3类似,但是对于MF超精细能级Table 5.The same as in table 3,but for the different MFof hyperfine sublevels.

3.2 超精细结构效应对圆极化的影响

表6给出了纵向极化电子碰撞类氦Sc19+离子(核自旋I=7/2,Fi=7/2)在1s2p3P2Ff→1s21S0Fi过程中不同超精细能级退激到基态辐射光子的圆极化度随入射能量的变化关系.为了便于比较,表中同时给出了Inal等[20]的理论结果.可以看到,不同超精细能级F组分上的圆极化度并不相同,同时各超精细能级F组分上辐射衰变的类型也不一样.以近阈值入射能量320 Ry为例,末态Ff=3/2→ Fi=7/2和Ff=11/2→Fi=7/2的辐射衰变均以磁四极M2跃迁占主导,所得的圆极化度Pc分别为0.1489和0.3872,而Ff=5/2,7/2,9/2→Fi=7/2的辐射衰变过程既满足磁四极M2跃迁同时也满足电偶极E1跃迁,且E1跃迁的概率相对较大,计算的磁四极M2跃迁圆极化度Pc分别为0.1063,0.1308和0.2797.因而,统计权重后,可以得到高电荷态类氦Sc19+离子(核自旋I=7/2)在1s2p3P2→1s21S0跃迁辐射衰变过程中最终所辐射出光子的圆极化度Pc=0.243,对比于精细结构层次上1s2p3P2→1s21S0磁四极M2跃迁辐射衰变的圆极化度Pc=0.891(由表2计算得到),超精细结构效应使得该线圆极化度减少了近72%,具有非常强的去极效应.这些结果与Inal等[20]利用扭曲波理论计算的结果符合得非常好.此外,除主要的电偶极禁戒M2(磁四极)跃迁之外,超精细结构还诱导了某些电偶极E1跃迁的发生,且电偶极E1跃迁占有较大分支比,是重要的衰变通道之一.例如,对于Ff=5/2→ Fi=7/2和Ff=7/2→Fi=7/2的跃迁过程,超精细诱导的电偶极E1跃迁光谱的的圆极化度分别为0.0306和0.0392.约为磁四极跃迁机制下的3%左右.而对于Ff=9/2→ Fi=7/2的E1跃迁,超精细诱导的电偶极E1跃迁光谱的的圆极化度达到了0.3138,超过了该线磁四极M2跃迁机制下的圆极化度0.2797.究其原因,还是核自旋破坏了精细结构层次上总角动量守恒,诱导了新的跃迁光谱.

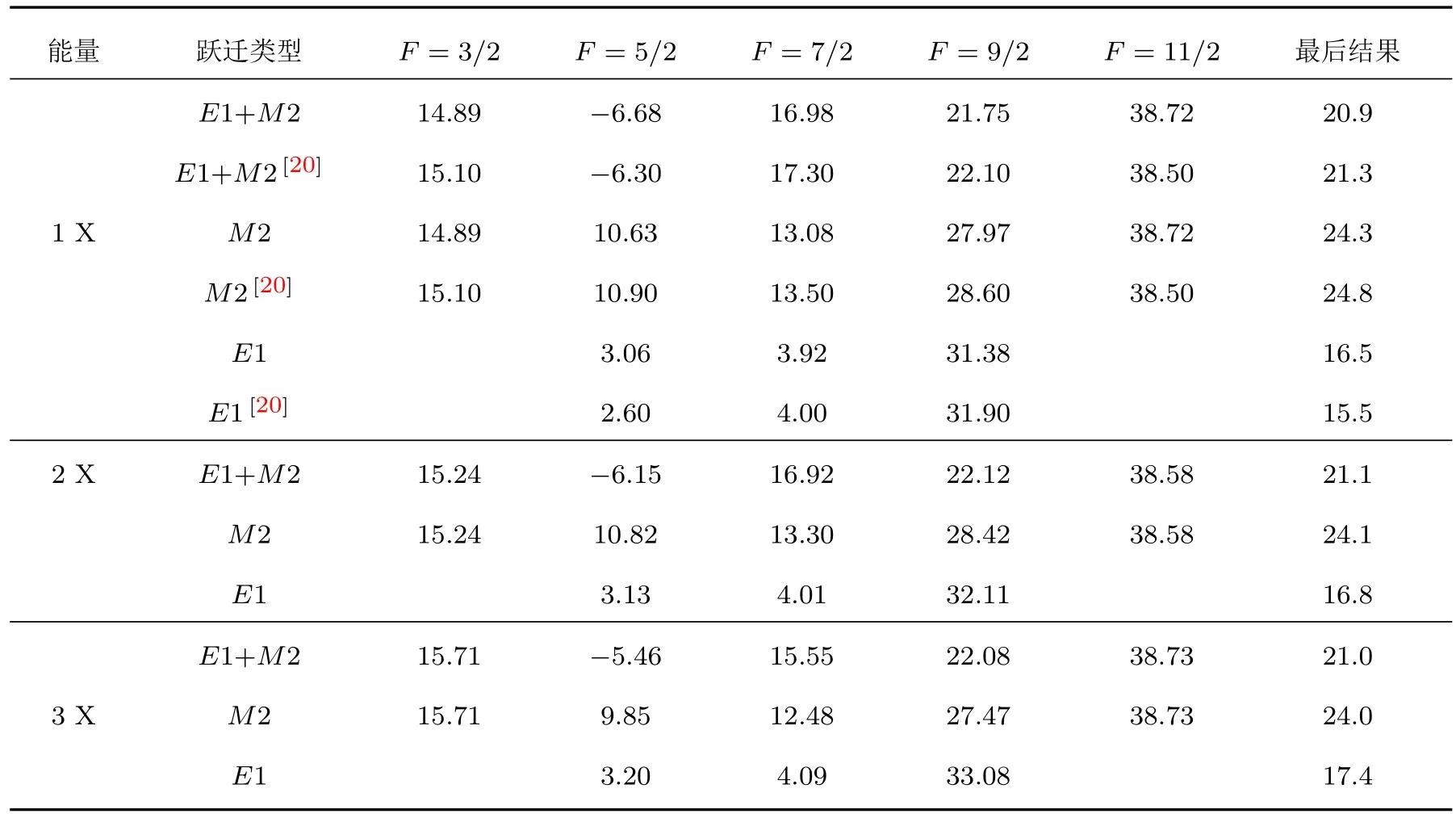
表6 超精细结构层次上类氦Sc19+离子1s2p3P2Ff→1s2 1S0Fi的圆极化度(%)Table 6.The circular polarization(%)of the 1s2p3P2Ff→1s2 1S0Fihyperfine-induced transition for He-like Sc19+ions following longitudinally polarized EIE process.

3.3 干涉效应对圆极化度的影响

任何一种跃迁概率占到总跃迁概率的1%时,不同跃迁类型振幅之间将会发生量子干涉.为了探讨超精细结构层次上E1-M2干涉效应对辐射光子圆极化度的影响,我们在表6中给出了Ff=5/2,7/2,9/2组分的考虑干涉效应的结果以及统计权重后的结果.作为比较,同时给出了Inal等[20]利用扭曲波计算的结果.可以看到,当纵向极化电子以近阈值能量320 Ry入射时,对于超精细组分Ff=5/2→Fi=7/2之间的跃迁过程,E1−M2干涉效应使得退激发辐射光谱圆极化度由0.1063变为−0.0668,减小了近40%,同时导致了符号发生相反的情况,具有较强的去极化效应.然而,对于超精细组分Ff=7/2→Fi=7/2之间的跃迁,E1-M2干涉效应使得圆极化度从0.1308变为0.1698,增大了近23%.因此,不难看出,占主导的磁四极M2跃迁通道和由超精细结构诱导的电偶极E1跃迁通道之间的量子干涉效应既能增大也能减少辐射光谱的极化度.这一现象与近期Surzhykov等[21]研究辐射电子俘获机制下形成的类氦离子1s2p3/21,3P2→1s21S0跃迁线非常类似.此外,我们发现,E1-M2干涉效应对纵向极化电子的能量并不敏感.例如,在近3倍阈值能量时,干涉效应使得超精细组分Ff=5/2→Fi=7/2之间的跃迁辐射光子的圆极化度从0.0985变为−0.0546,减小了近43%,而使得超精细组分Ff=7/2→Fi=7/2之间的辐射光子的圆极化度从0.1248变为0.1555,增大了近20%.这些贡献的大小与近阈值入射能量320 Ry情况下基本相同.由此可见,干涉效应导致光谱极化的加强或减弱依赖于特定的跃迁类型和初末态总角动量.另一方面,可以看到,考虑超精细结构各组分统计权重后纵向极化电子碰撞类氦Sc19+离子(核自旋I=7/2,Fi=7/2)在1s2p3P2Ff→1s21S0Fi过程中的结果与Inal等[20]的计算结果符合得非常好.

3.4 Breit相互作用效应对圆极化度的影响

图1 E1-M2量子干涉效应对退激发辐射X射线光子极化特性的影响Fig.1.Influence of E1-M2 quantum interference on the polarization of the X-ray photoemission.

为了更清晰地反映超精细层次上E1-M2量子干涉效应对退激发辐射X射线光子极化特性的影响,图1给出了纵向极化电子碰撞激发类氦205Tl79+离子1s2p3P2→1s21S0过程中超精细诱导的Ff=3/2→Fi=1/2退激发辐射光子的圆极化度随入射电子能量的变化关系.图中,NB表示仅包括库仑排斥相互作用时的相对论计算结果,B表示包括库仑和Breit相互作用时的相对论计算结果.由图1(a)可见,在纯电偶极E1跃迁情况下,超精细诱导的Ff=3/2→ Fi=1/2退激发辐射光子具有较大的圆极化度,且随着入射电子能量的增大保持不变,这些特征与Inal等[20]在精细结构层次上对类氦Fe24+离子1s2p3P2→1s21S0磁四极M2线研究得到的结论非常相似.在他们的研究中该线近乎于完全圆极化,且不依赖纵向极化电子的能量.E1-M2干涉效应使得超精细诱导的Ff=3/2→Fi=1/2退激发辐射光子的圆极化度减小到0.3左右,相对于纯电偶极E1跃迁圆极化度0.7减少了近55%,相对于纯磁四极M2跃迁圆极化度0.5减小了近40%.此外,为了评估E1-M2之间干涉项的贡献,在图1中我们还给出了不考虑干涉项E1-M2统计权重后的计算结果,其圆极化度曲线处于纯E1跃迁和纯M2跃迁之间为0.53.不难看出,E1-M2干涉效应导致圆极化度的减小很大程度上依赖于E1-M2之间的干涉相互作用.事实上,对于中性原子及高电荷态离子,要获得准确的碰撞动力学过程的信息,在计算中除了包括电子间的静电库仑排斥相互作用,还必须包括电子间的磁相互作用和延迟效应贡献.为了探讨Breit相互作用效应在超精细层次上对退激发辐射X射线光子极化特性的影响,我们在跃迁矩阵元中加入了Breit相互作用算符,并计算了磁子能级碰撞强度进行了相应的转化.图1(b)给出了考虑Breit相互作用后,纵向极化电子碰撞激发类氦205Tl79+离子1s2p3P2→1s21S0过程中超精细诱导的Ff=3/2→ Fi=1/2退激发辐射光子的圆极化度随入射电子能量的变化关系.结合图1(a)可以看出,这两种计算情况下的碰撞激发总截面都随入射电子能量的增加以相似的方式缓慢减小.Breit相互作用使得不同类型跃迁对应的圆极化度在目前能区内都减小,同时两种情况下的差别随着极化电子能量的增加变得越来越明显.例如,在阈值附近,Breit相互作用效应使得纯电偶极E1跃迁的圆极化度由0.7减少到0.5,使得纯磁四极M2跃迁的圆极化由0.48减少到0.22.另一方面,Breit相互作用效应对考虑干涉效应后的结果也产生了重要影响.使得考虑超精细诱导的Ff=3/2→Fi=1/2退激发辐射光子的圆极化度由0.3进一步减少到0.1.这些变化规律意味着在高能电子与高Z离子的碰撞激发过程研究中,Breit相互作用必须予以考虑.

4 结 论

利用相对论多组态Dirac-Fock方法和密度矩阵理论,系统研究了超精细结构效应对退激发辐射光子圆极化特性的影响. 计算了纵向极化电子碰撞激发类氦Sc19+和205Tl79+离子在1s21S0→ 1s2p3P2过程中精细结构层次上的碰撞强度,进而转化得到超精细结构层次上的MF磁子能级布局情况.获取了不同超精细能级之间辐射衰变过程中发出的特征光子的极化特性,同时讨论了超精细诱导跃迁的贡献,分析了E1-M2量子干涉效应和Breit相互作用效应对超精细诱导跃迁辐射衰变过程放出光子极化特性的影响.研究发现:超精细结构效应,E1-M2量子干涉效应以及Breit相互作用效应均具有较强的去极化作用,能较大地消减辐射光子的极化度.例如,在近阈值能量入射情况下,超精细结构效应使得类氦Sc19+离子在1s2p3P2→1s21S0磁四极跃迁辐射衰变过程中所辐射出光子的圆极化度减少了近72%.E1-M2干涉效应使得类205Tl79+离子在1s2p3P2→1s21S0超精细诱导的Ff=3/2→Fi=1/2退激发辐射光子的圆极化度相对于纯磁四极跃迁减小了近40%.Breit相互作用效应使得类205Tl79+离子在1s2p3P2→1s21S0超精细诱导的Ff=3/2→Fi=1/2退激发辐射光子的圆极化度相对于纯磁四极跃迁减小了近50%.我们希望随着X射线极化测量技术的不断升级,这些强的高阶物理效应能进一步在储存环或EBIT装置上得到证实.