四极杆电极系统的应用与研究进展
徐福兴,杨 凯,王 强,赵 欣,陈 斌,丁传凡
(1.复旦大学化学系激光化学研究所,上海 200433;2.中国环境监测总站,北京 100012)
四极杆电极系统的理论与应用是20世纪50年代末发展起来的全新的科学领域[1]。由于离子在四极电场中具有特殊的运动性质,四极杆电极系统已被广泛地用于制造多种分析科学仪器,如四极杆质量分析器[2-3]、四极线性离子阱[4-8]、四极杆离子导引[9]以及四极杆与其他各种质量分析器组合而成的复合型高性能质谱分析仪器等。这些质谱仪器在科学研究、环境保护、食品卫生、国土安全等领域内的广泛应用,不仅极大地推动了科学和技术的进步,还促进了质谱学理论和技术本身的发展[8-11]。在过去的半个多世纪里,四极质谱领域内的科学家在四极杆电极结构与四极场的产生、离子在包括各种高阶电场的四极场中的运动规律、四极杆质量分析器的结构与性能、新型四极离子阱质量分析器的理论与应用、高极场的产生以及对质谱性能的影响等诸多方面进行了大量的理论与实验研究,其结果不仅极大地丰富了质谱学理论,也产生了一批有广泛应用价值的新型四极质谱仪。
本工作首先简要介绍四极杆电极系统的工作原理,离子在四极电场中的运动规律;再进一步说明四极杆电极系统的几何结构与质谱性能的关系,以及近年来有关高阶场的产生及其对质谱分析性能的影响等;然后再分别介绍国内外在四极杆质量分析器和四极离子阱质谱领域内的最新研究成果;最后对四极杆电极系统发展方向作简要的展望。
1 四极杆电极系统的理论
1.1 四极杆电极系统与四极电场的产生
四极杆电极系统的理论是由Paul等[1]于1958年创立的,根据他们的假设和理论研究,证明了可以在一定空间内产生“纯净”理想四极电场分布的四极杆电极系统,但必须是由4根几何形状完全等同,且包含双曲面截面的电极平行围绕着一个中心对称轴合围而成,其系统结构示意图示于图1。
如图1a所示,此4根双曲面电极平行且对称地固定在一起,均匀的围绕在一个半径为r0的同心圆四周,该同心圆通常被称为四极杆电极系统的场空间。此四极杆电极的截面示意图示于图1b,4根双曲面电极的截面与它们所围成的场空间在二维空间的分布满足方程1。
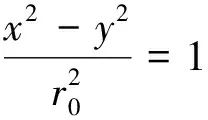
(1)
在实际使用中,4根电极中相对的2根电极被连接在一起,形成一对X电极和一对 Y电极。四极杆电极系统的工作电源为一同时包含高频交流电压和直流电压成分的所谓射频电源(radio frequency, RF),四极杆电极上的电势φ0可由式2计算:
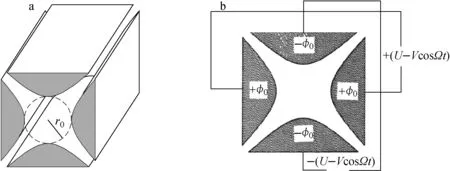
注:a.电极结构示意图;b.电极截面示意图图1 四极杆电极系统组成结构示意图Fig.1 Schematic diagram of quadrupole rodset
φ0=±(U-VcosΩt)
(2)
式中,φ0为加载在四极杆电极上的电势,U为RF 电源中的直流电压成分,V为RF 电源中的交流电压成分,Ω为射频电源的角频率,t为时间。
当射频电源的正、负输出电压分别加载在一对X电极和一对Y电极上时,在四极杆电极所围成的场空间内会产生如下形式的四极电场分布:
(3)
离子在时间相关的四极电场中的运动是四极杆电极进行离子束缚和质量分析的基础。
1.2 离子在四极电场中的运动及其稳定区图
离子在四极电场中的运动可以根据牛顿第二定律求解。有关离子运动的Mathieu 方程的详细求解过程可以参考文献[3],这里只简要给出2个重要参数a和q的计算式:
(4)
由a和q绘制的离子在四极电场中的稳定区图示于图2,这是理解四极杆质量分析器、四极离子阱和四极杆离子导引的理论基础。
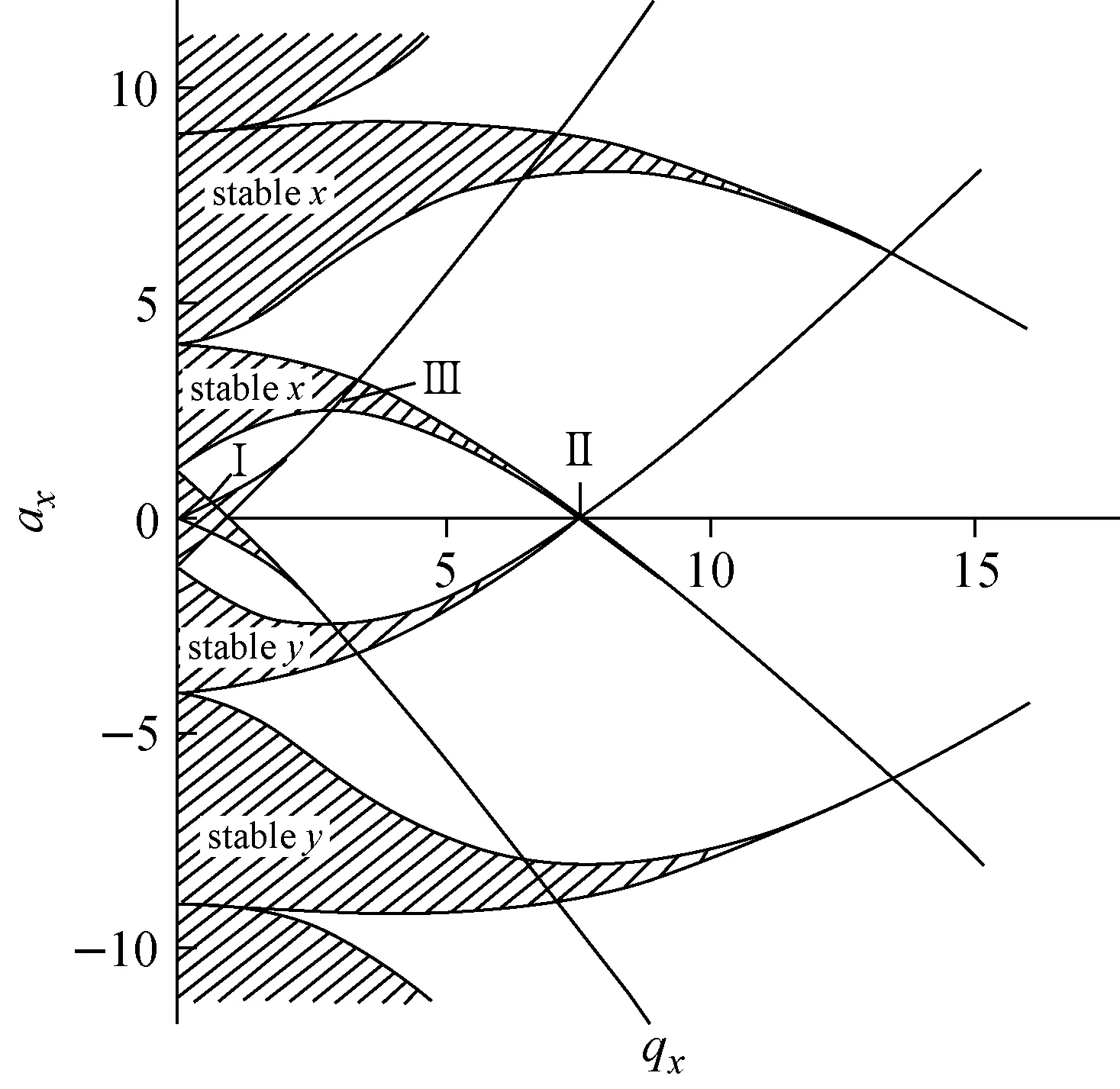
图2 离子在四极电场中的稳定区图[4]Fig.2 Stability diagram of ion in quadrupole field
在场半径为r0的四极杆电极系统中,离子的运动状态完全取决于用于产生电场分布的射频电源RF(包括直流电压U,交流电压V和电源频率Ω)。离子在四极电场中的运动可分为稳定和不稳定两种情况。离子的稳定运动是指,当t→∞时,离子在x-y方向上的一个有限范围内运动。离子的不稳定运动是指离子的运动轨迹在x-y方向上随时间逐渐增大,直至最后逸出场空间。很显然,稳定运动的离子可以到达安置在四极杆后的离子探测器并被检测到,得到质谱信号。
在只含有四极电场成分的四极质量分析器中,离子在x和y方向上的运动是相互独立的,因此,离子的稳定运动是指离子在这两个方向上的运动都稳定。离子在x方向上稳定与否取决于ax和qx;同样地,离子在y方向上稳定与否取决于ay和qy。对四极场中的离子,当其ax和qx,ay和qy都在某个有限的范围内时,即离子在x和y方向上的运动都为稳定运动时,离子在四极场中的运动才是稳定的。也就是说,只有当某种m/z离子的a和q都落在稳定区内时,离子才是稳定的。由于ax=-ay、qx=-qy,离子在x方向上的稳定图与离子在y方向上的稳定图是相对于x轴呈对称分布的。
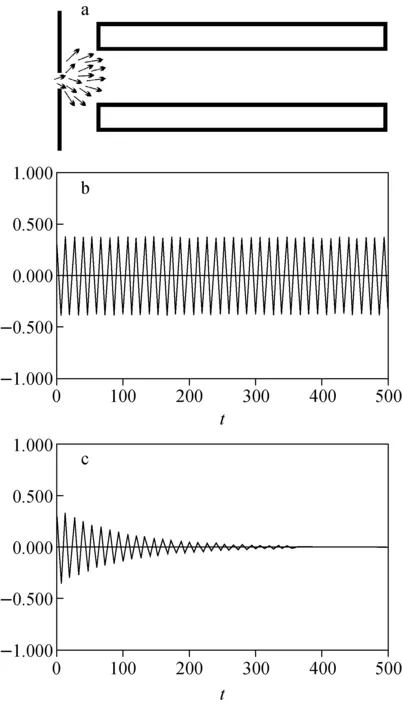
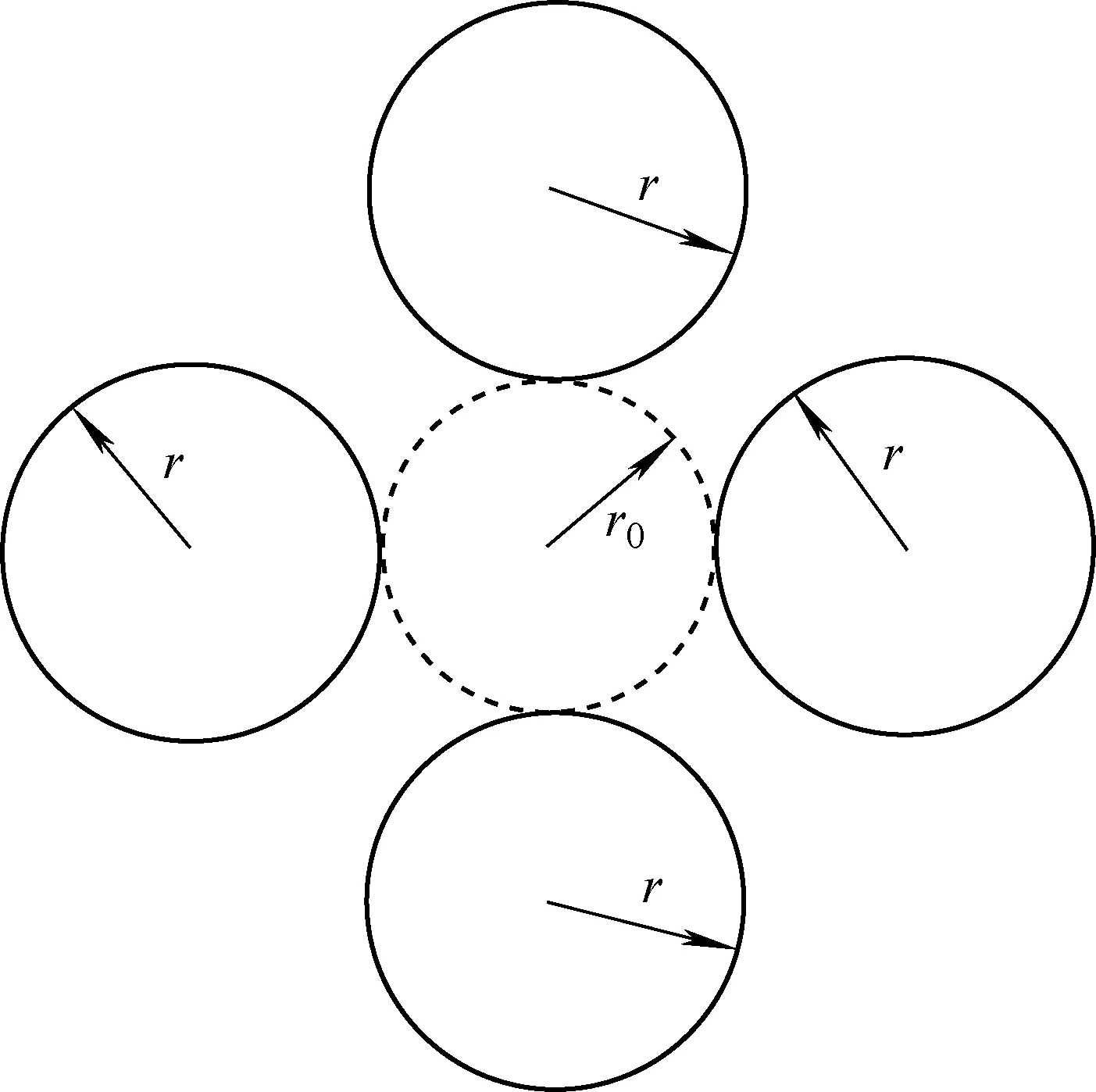
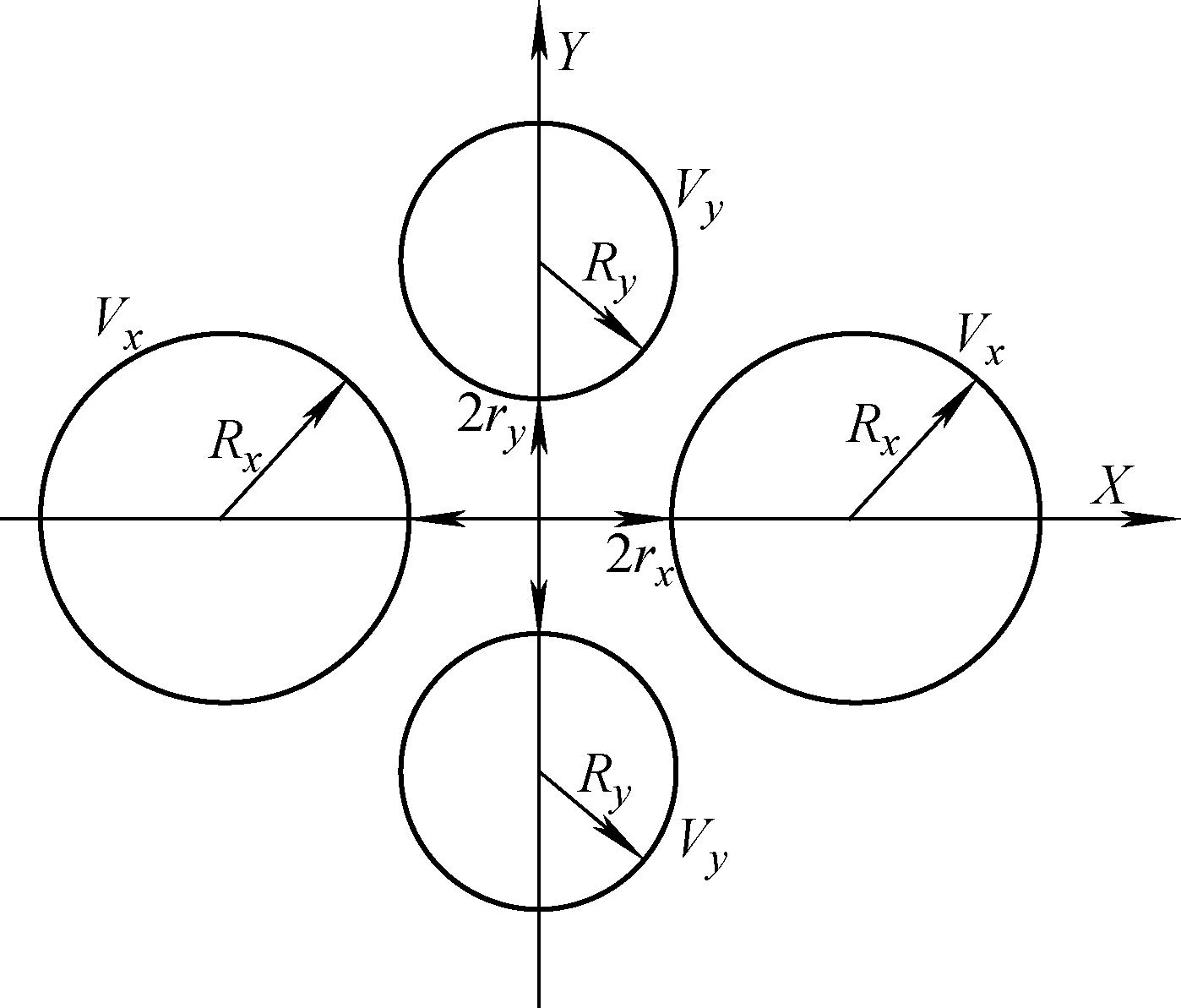
从图2可以看出,对应于离子的稳定运动有很多个稳定区,即x方向上的稳定图与y方向上的稳定图重合的区域,如Ⅰ、Ⅱ、Ⅲ等区域。所有的稳定区都可以被用作四极质谱的工作区。目前常用的四极杆质量分析器和四极离子阱质谱仪都工作在第一稳定区,示于图3。第一稳定区的a和q的范围分别为:0 图3 四极杆电场的第一稳定区图和离子扫描线示意图Fig.3 The first stability region of quadrupole field and the scan line of mass analysis 四极杆电极系统已被广泛地用于搭建各种分析科学仪器,但其基本的功能只有3种,即四极杆质量分析器、四极杆离子导引和四极线性离子阱,下面分别对其性质加以描述。 四极杆质量分析器是四极杆电极系统的一个主要应用,它的工作原理可以用第一稳定区图加以解释。对于一个几何结构和工作电源都确定的四极杆电极系统,当一个离子进入四极杆的场空间时,它对应于稳定区图中的位置坐标可以由式4计算,即: 如果(am,qm)落在第一稳定区内,该离子最后可以通过四极杆电极系统,并被设置在四极杆后面的离子探测器检测到,形成与其对应的质谱峰;反之,如果(am,qm)落在第一稳定区外,则此离子在x-y方向上的运动半径越来越大,最后将逸出场空间,无法被离子探测器检测到。很显然,如果实验过程中连续改变工作电源的直流和交流电压U和V,使得在某一时刻只有某一质荷比的离子可以通过四极杆电极系统,而在全部实验过程中,分别记录样品中所有质荷比的离子信号,则可获得对于各种质荷比离子的质谱峰,或称之为质谱图。这就是四极杆电极可以用于质量分析的基本原理。 在四极杆质量分析器性能参数中,质量范围和质量分辨率是两个最基本最重要的参数,下面将分别讨论它们与四极杆电极系统工作参数之间的关系。 2.1.1质量范围 一台四极杆质量分析器的质量范围是指其可以测量的最小离子与最大离子,可由式(5)估算: (5) 从理论上讲,一个四极杆质量分析器的质量测量上限是无止境的,只要其工作电压无限大就可以了。但由于电子技术,特别是生产射频电源的电子元器件的限制,一个商用质谱的工作电源的输出电压是有限的,因此,任何一台四极杆质谱的质量测量范围也是有限的。例如,对于一个四极场直径为2r0=10.52 mm(对应的四极杆直径约为2r=12 mm)的四极质量分析器,若其RF电源的工作频率为1 MHz,最大输出电压为2 000 V,所能测量的最大m/z离子为: 1 000 Da 从式(5)还可以看出,除了提高RF电源的电压外,还有2种方法可以提高四极质量分析器的质量分析范围:一是使用半径较小的四极杆电极;二是使用较低输出频率的RF电源。但较小直径的四极杆和较低频率的RF电源会带来其他问题。在实际应用中,只要质谱仪的质量测量范围可以涵盖被测量样品中的所有目标分子大小,则可满足要求。 2.1.2质量分辨率 简单地说,质谱仪的质量分辨率是指其将不同离子的质谱峰分辨开来的能力。比如说,分辨率为1 000的质谱仪应该可以将m/z1 000 和m/z1 001两个质谱峰区分开。 质谱仪的质量分辨能力一般用M/ΔM表示,M为质量数,ΔM为相应的质谱峰的宽度,它可以是半峰高处的宽度,即所谓的全高半宽(FWHM),也可以是10%或20%峰高处的宽度。 根据前面讨论的四极杆质量分析器的工作原理,当进行质量分析时,获得有分辨的质量分析是指,在某一实验条件下,只有一个m/z离子可以稳定地通过四极杆电极到达离子探测器,而大于或小于指定m/z的离子都无法通过四极杆电极。实验过程中,四极质谱仪是通过连续扫描其工作电源的U、V电压值及其比值U/V来实现离子质量分析。由于U/V=a/2q,它对应于第一稳定区上的一条直线,平常被称为扫描线。如果对应于某种离子的扫描线与稳定区图不相交,则表明此离子在四极杆电极中的运动是不稳定的;反之,如果对应于某离子的扫描线与第一稳定区相交,则此离子的运动是稳定的,可以被测量到。图3中的(q1,q2)和(q3,q4)分别表示两条扫描线与第一稳定区的交点。 下面进一步讨论离子扫描线的设定与质谱分辨的关系。扫描线1所对应的质谱条件下的质量分辨能力可以表示为: (6) q=0.706是稳定区图顶点的坐标。因此,对一个具有理想四极场分布的四极杆质量分析器来说,其质量分辨能力可以很大,实验中只要调节U/V值,使扫描线的两个交点之差很小就可实现。如扫描线2的两个交点之差(q4-q3)比扫描线1的(q2-q1)要小,表明利用扫描线2可以获得更高的质量分辨。 在实际应用过程中,一个四极质谱的质量分辨能力总是有限的,其原因主要有3点:第一,上述四极场理论,离子在四极场中的运动规律,以及稳定区图的获得等都是建立在离子在完美四极场中的运动。但由于机械与电子加工精度的限制,理想双曲面电极系统以及理想RF电源是达不到的。电极结构的几何误差将导致高极场成分的产生,而高极场成分将直接导致质量分辨能力的下降。第二,由于四极杆电极的长度有限,离子在四极场的运动时间也是有限的。第三,四极杆电极的两端与其他电极之间会产生所谓边缘场的影响。 首先讨论四极杆电极的几何误差对质量分辨的影响。四极杆电极的几何误差将直接导致场半径的改变。根据式(5)有: (7) 所以 (8) 假定四极杆电极系统的场半径r0=5 mm,则获得M/ΔM=1 000质量分辨时,r0的最大偏差Δr0=0.002 5 mm。也就是说,只有在四极杆电极的几何加工精度和机械装配精度都小于2.5 μm的情况下,才能实现1 000的质量分辨能力。这对现有的机械加工水平是一个很大的挑战。 第二,四极杆的长度。根据前面的讨论可知,离子稳定运动是指离子在t→∞的时间范围内都是稳定的。但由于四极杆的长度是有限的,故离子的运动时间也是有限的。离子在四极场的运动时间将直接影响四极杆的质量分辨能力。由于离子在四极杆中的运动时间与离子的初始动能、四极杆的长度、RF电源的频率有关,故常常用离子在四极杆中的运动周期数N来讨论它们对质量分辨的影响。假定离子在四极杆中的运动周期为N,离子质谱峰的半高宽为R1/2,则有: (9) 式中h为常数。对于工作在第一稳定区中的四极杆质量分析器,Paul等[1]计算出h=12.25,而Austin等[12]则认为h=20。 根据式(9),不论h值为多少,提高离子在四极杆系统中的运动周期数N都是提高质量分辨能力的有效方法。 提高N的方法有以下几种:1) 使用较长的四极杆电极,如Von Zahn[13]通过使用长度为 5.82 m的四极杆电极系统获得了数千的质量分辨率;2) 减小离子的初始动能,即减小离子的初始运动速度,使得离子在有限长度的四极杆电极系统中有更长的运动时间,即有更多的运动周期数N;3) 采用更高频率的RF电源,以增加离子在四极杆中的运动周期数,但由于高频率的RF电源在相同的输出电压下会降低质量分析范围,这种方法在质量范围要求不高的ICP-MS中被广泛使用[14]。 第三,边缘场效应。不论四极杆电极有多长,其2个端点都设置有其他形状的电极,以保证样品离子的引入和引出。因此,四极杆电极的两端与其他电极之间会形成边缘电场分布,它同时受四极杆电极和两端其他电极的影响。换言之,接近四极杆电极两个端点的电场分布一定不是纯四极场成分,即同时混合了四极场和其他成分的电场,这种电极端点附近的复杂电场分布通常被称之为“边缘场”。前人的研究结果表明[10,14],边缘场的分布范围沿四极杆的径向方向大约为r0。边缘场的存在对四极杆性能的影响主要表现为降低四极杆电极的离子引入效率和质量分辨能力,其解决方法之一是在四极杆质量分析器前安装所谓的预四极杆[10]。 四极杆电极系统的另一个重要应用是四极杆离子导引(quadrupole ion guide),它的作用是将离子聚焦成离子束,使之朝一个方向运动,以减少离子在传输过程中的损失,实现样品的高灵敏度分析。四极杆离子导引被广泛地用于各种质谱仪器中,将由多种离子源,特别是包括电喷雾电离离子源等大气压电离源产生的样品离子传输到质量分析器中。 四极离子导引与四极杆质量分析器的工作原理都是基于四极场理论,它们的共同点是利用四极电场来聚焦和束缚离子,但它们的最大区别在于:四极杆离子导引的作用是高效地传输几乎所有的样品离子,因此它没有质量分辨能力。即,在四极杆离子导引中,尽可能使所有的离子运动都是稳定的,都能够穿过四极杆电极系统而到达下一个部分。四极离子导引的一些基本性质同样可以用第一稳定区图来理解。 2.2.1质量范围 四极杆离子导引的一个最基本性质就是它的质量范围,即可以传输的离子质荷比范围。下面根据第一稳定区图和式(5)来加以分析。 根据第一稳定区图,要想实现最大质荷比范围的离子传输能力,离子扫描线与第一稳定区图的交点范围越大越好,从图中可以看出,最大的交点范围为0.908-0=0.908。实现这样一个扫描线的方法就是设定a=0,即使得RF电源的直流输出为0。当用四极杆电极系统作离子导引时,其工作电源为不含有直流电压成分的RF电源,即其工作电源为: Φ=VcosΩt (10) 通常情况下,除了四极质谱(包括三重四极质谱)的离子导引外,加载在四极杆质量分析器上的RF电压的直流电压V和频率Ω都是不变的,所以离子导引的质量范围可由式(5)进行分析、计算:最大的m/z对应于最小的q值,最小的m/z对应于最大的q值。 当a=0时,离子在第一稳定区内的坐标仅由q值决定,而q=0-0.908,因此: (11) 由式(11)可知:q=0,m/z=∞,因此可以被导引的离子是没有质量上限的。虽然从理论上来讲,q=0~0.908,但实验结果表明,当q值很小时,相应的较弱电场对离子束缚能力很差,故有实际应用价值的q值应大于0.006。所以对任何一个四极杆离子导引来说,有效的离子传输范围可根据其RF工作电源的直流电压V和频率Ω,以及q=0.006~0.908求得。 四极杆离子导引的质量下限除了受q=0.908所限外,还取决于RF工作电压。例如,当用V=1 000 V,Ω=106Hz的RF电源驱动r0=0.005 m的四极杆离子导引时,通过公式(5)可以计算出最小m/z的离子为: 4.463 5×10-6kg/C≅430 Da 理论上,降低离子导引质量下限的方法很简单,即降低RF电源的工作电压。但由于四极电场对离子的束缚能力与工作电压有关,所以电压的选择并不是越低越好。 这里需要特别指出的是,由于四极杆离子导引的作用是传输离子,它不需要考虑质量分辨的问题,也就是说,高极场效应在这里已完全不需要考虑。因此,作为离子导引使用的四极杆电极系统,其可能引入高极场成分的电极杆机械加工精度和组装精度已不是问题。更进一步,由于高极场成分往往对离子有更强的束缚能力,它们的存在对提高离子导引能力是有益的,在某些情况下,以产生高阶场为主的六极杆电极系统,八极杆电极系统可以更好地传输离子。这就是为什么除四根双曲面型电极,圆柱型电极可以作为四极杆离子导引外,可以产生众多高极场成分的矩型电极等同样可以作为离子导引杆使用。 相比于传统的离子光学系统,如离子聚集透镜、离子偏转装置等,四极杆离子导引的一个最大优点是,它不需要有高真空的工作环境,因此特别适合将由大气压电离源产生的离子高效引入到高真空环境中,以满足需要高真空工作条件的各种质量分析器分析使用。 2.2.2离子聚焦和传输 四极杆离子导引的主要作用是聚焦和传输离子,因此它对离子的聚焦能力和传输效率是最重要的。下面分别讨论离子聚焦和传输作用的原理和影响因素。 四极杆离子导引传输和聚焦离子示意图示于图4。离子聚焦是指离子在四极杆离子导引中逐渐向场中心,即向四极杆中心轴聚集。离子在进入四极杆电极前都具有一定的初始动能和速度,以及几乎为180°的角度分布,示于图4a。也就是说,离子进入四极杆电极时,在垂直于中心轴的方向上有一个速度或能量分布。 注: a.离子进入四极杆时的运动状况示意图;b.无碰撞情况下的离子运动状况模拟结果;c.碰撞聚焦情况下的离子运动状况模拟结果图4 四极杆离子导引传输和聚焦离子示意图Fig.4 Diagram of ion transmission and focus using a linear quadrupole 但从理论上讲,四极场并不能聚焦离子,这是因为离子在四极离子导引中并没有从周期性变化的RF电源产生的电场中获得或失去能量,因此,它在垂直于中心轴的方向上的总能量(动能和势能的和)及其运动范围是不变的,即离子做周期运动的振幅是不变的,无法产生聚焦结果,其模拟情况示于图4b。如果希望离子在导引杆中聚焦,则必须使离子在垂直于四极杆轴线方向上的能量减少。实验中减少离子动能的方法很简单:在四极杆离子导引区引入适当压力的气体,如空气,或充入一定的He或Ar气,使得样品离子在四极杆中与这些气体分子不断地发生碰撞而失去动能,从而逐渐向中心聚集。在绝大多数实验过程中,只要使四极杆离子导引区的真空度不要太高就可以了,如真空度保持在0.133~0.013 3 Pa。分子碰撞对离子聚焦作用的模拟结果示于图4c。 当离子被四极场束缚在四极杆中并经碰撞聚焦后,离子传输就很容易了。从理论上讲,离子在离子导引中的传输是无损失的,即四极杆离子导引可以有100%的传输效率。 四极线性离子阱质量分析器是四极杆电极系统的另一个重要应用,其工作原理同样是基于四极场理论,也可以用第一稳定区图加以解释。四极离子阱[15-19]是一种可以存储离子的实验装置,实际上它既可以用于存储离子,也可以用于离子的质量分析。根据电极形状的不同, 四极离子阱可以分为三维离子阱和线性离子阱两种。三维离子阱是由1个环电极和2个端盖电极共3个电极组成的,出于文章篇幅的考虑,这里不做介绍,有兴趣的读者可参考文献[3,18]。下面只简单介绍由四极杆电极组成的线性离子阱的结构、原理及其研究现状。 传统的四极线性离子阱是由4根双曲面电极组成,它的空间几何结构、产生四极场的原理及其离子在场空间的运动规律与前面陈述的四极杆质量分析器基本相同。四极杆电极系统作为离子阱使用时,其最大的不同在于,在四极杆电极的2个端点放置2个电极,这2个电极上的电压配置应使得在四极离子阱电极中形成一个直流电势阱,将四极杆区域的离子束缚在四极杆电极和直流电势阱的离子存储区域中。 同样地,为了机械加工和组装的方便,四极线性离子阱同样可以用4根圆柱形电极构成,它的原理和作用几乎与由双曲面电极所构成的离子阱没有差别。 离子阱质谱除了具有其他质谱仪所共有的高灵敏度、高质量分辨能力外,还同时具有离子存储和串级质谱分析的功能,使得人们可以在一种单一的质谱仪上同时实现质谱分析和串级质谱分析,以同时获得有关样品组成和分子结构的多重信息。此外,离子阱质谱由于其结构简单、易加工、能耗小、工作气压高等优势,在质谱小型化过程中扮演着重要的角色。因此有关新型离子阱的研究和开发一直是大家感兴趣的课题。近年来,几种新型的离子阱质量分析器先后被开发出来,但由于篇幅所限,这里不做详细介绍。 四极场理论是建立在由4根双曲面形电极所组成的四极杆电极系统基础上的,但在实际应用中,4根高精度双曲面电极的加工和组装是非常具有挑战性的。因此,寻找几何结构更加简单的柱状电极替代双曲面形电极组建四极杆质量分析器是过去几十年来科学家们追求和研究的主要目标之一。圆柱形电极已成为目前构建商业四极杆质量分析器的主要方法之一。 从理论上讲,圆弧面与双曲面是比较接近的两种几何形状,但当使用圆柱形电极取代双曲面形电极构建四极杆电极系统时,还必须考虑4根圆柱形电极的相对空间位置,以确保产生最接近于理想四极场的电场分布。关于4根圆柱形电极组建四极杆电极系统的方法与产生电场分布的关系前人已有大量的研究[20-22],其主要结果有:1) 由于理想四极杆电极系统的4根双曲面电极是等同的,所以4根圆柱形电极也必须是等同的;2) 由于4根圆柱形电极组成的四极杆电极系统将产生除四极场之外的高极场,如十二极场A6、二十极场A10等,这些高极场成分将直接影响四极杆系统的质量分辨能力。因此圆柱形电极的半径r和与之所合围而成的场半径r0必须满足一定的比例条件才能获得最佳的质量分辨能力,其结构示意图示于图5。Dayton等[23]认为当r/r0=1.148时有最佳的结果,而Lee-Whiting等[24]根据计算认为r/r0=1.145 11为最好,Denson等[14]的计算结果为r/r0=1.146 8,而Douglas等[21]的研究结果则与Reuben等[25]关于圆柱形四极杆存在高阶场的研究结果一致。 上述研究都是基于获得A6=0的四极杆电极几何结构,而最近的研究表明,当A6和A10的大小可以相互抵消,同样可以获得较好的质量分辨。基于这个假设,Schulte等[26]得到r/r0=1.10,而Gibson等[27]通过模拟比较双曲面电极和圆柱型电极所获得的质谱峰形状,认为r/r0=1.148为最佳。 图5 圆柱形电极四极杆结构示意图Fig.5 Schematic diagram of quadrupole system with four cylindrical rods 后来,Gibson等[28]又进一步研究了r/r0值对质谱分辨的影响,认为r/r0=1.12~1.13都可以给出较好的结果。Douglas等[20]的理论模拟计算结果也表明r/r0=1.128~1.130将给出满意的离子传输效率和质量分辨能力。综合前人的研究,其出发点有二:一是获得十二极场为零的场分布,即A6=0;二是获得大小基本相等的十二极场和二十极场分布,即A6=-A10,使得它们对离子的影响相互抵消。由于高极场对粒子运动的影响到目前为止还不能给出精确的解析解,特别是当多种高极场同时存在时,离子的运动状况还无法从数学上准确求解,因此可以预料,有关这类问题的研究还将继续成为四极质谱领域内大家感兴趣的问题之一。 由前面的论述可知,四极杆电极系统中高极场的产生是不可避免的,而高极场成分的直接后果是导致四极质量分析器的质量分辨能力下降。 前人在如何降低高极场成分对质量分辨能力的影响方面已做了大量的理论和实验研究,特别是用圆柱形电极取代双曲面电极作质量分析器时,如何降低十二极场(A6)和二十极场(A10)对质量分辨的影响已有大量报道。但由于目前物理学理论和数学方法的限制,还很难从理论上精确描述离子在高极场,特别是当多种高极场同时存在时的运动规律。因此,有关高极场成分对四极杆电极系统质量分辨能力、离子传输效率等的影响,还主要依赖实验结果,或数值近似模拟计算。近年来,随着质谱学研究的深入,有关高极场效应的研究有了进一步的发展,下面简要介绍有关六极场和八极场对四极质谱性能的研究进展。 3.2.1六极场成分对四极质谱性能的影响 有关六极场的产生方法是由Douglas等[29]于2003年首先提出的,他们发现如果将构成四极杆电极系统的4根圆柱形电极中的一对电极,如两根y方向上的电极同时向x方向旋转一定的角度,则可产生除四极场外的少量六极场(A3),且六极场成分的多少与该对电极旋转的角度有关。换句话说,可以通过控制电极的旋转角度来控制四极场中六极场的多少。 Konenkov 等[29]对加入六极场的四极杆系统的质量分析性能做了理论上的探讨,发现如果在四极场中加入2%的六极场,可以获得约1 130左右的质谱分辨;而当在四极场中加入8%、12%的六极场后,四极杆质量分析器的质谱分辨将下降到几百以内,并且其质谱峰的对称性也会变差。 Douglas 等[30]通过实验仔细研究了含一定六极场的四极杆电极系统的质谱性能,发现当加入4%的六极场至四极场中时,不论是用常规的质量分析方法,还是采用所谓的稳定岛质量分析方法,或者是质量选择性轴向逐出方法,都可以获得高于2 000的质量分辨能力。 3.2.2八极场成分对四极质谱性能的影响 Sudakov等[31]于2003年发现,当使用两组直径大小不同的圆柱形电极,如2个直径较大的Y电极和2个直径较小的X电极,组建四极杆电极系统时,将产生除四极场之外的八极场成分(A4),且八极场成分的多少与两对电极的半径大小比例有关。它们的半径差别越大,加入的八极场成分越多。八极场四极杆电极系统示意图示于图6。 Ding等[20]的实验结果发现,当使用含八极场成分的四极杆系统进行质量分析时,如果将RF电源的直流电压成分加载在较大直径的一组电极上,只可获得100多的质量分辨能力,并且其离子透过效率也很低;但如果将RF电源的直流电压成分加载在较小直径的一组电极上,则可获得高于5 800的质量分辨能力,并且其离子透过效率在低于1 000时比不含八极场的四极杆系统高出50%,说明在四极场中加入适量的八极场成分不仅可以获得高分辨的质量分析结果,还可以显著提高四极杆电极系统的离子传输效率和分析灵敏度。Konenkov 等[32]还从理论上探讨了含八极场成分的四极杆电极系统的质谱性能,如八极场成分对第一稳定区图的影响等。Moradian等[33]进一步研究了利用所谓的稳定岛进行质量分析的方法,和利用质量选择性轴向逐出方法研究加入八极场的四极杆系统的质量分析性能。 图6 八极场四极杆电极系统示意图[31]Fig.6 Schematic diagram of a quadrupole system with added octopole field[31] 人们通过对六极场,八极场成分的研究,不仅丰富了四极质谱学的理论,还进一步拓宽了四极杆电极系统的实际应用前景。相信随着科学和技术的不断进步,有关其他高极场成分,如十极场、十二极场、二十极场等对离子运动和质谱性能的影响也一定会不断深入[28]。 自20世纪50年代四极杆电极系统被发明以来,已被广泛应用于制造四极质量分析器、四极杆离子导引和四极线性离子阱等。在过去的近70年时间里,有关四极质谱的理论,从电极结构、电场的产生与电极结构的关系、离子在电场中的运动规律,到电场分布对质谱质量分辨的影响,以及四极杆电极系统与其他质量分析器的结合都有大量的研究和探索,建立了比较完整的四极质谱理论,产生出一个又一个有实际应用价值的新仪器,新技术和新方法。 但基于以下3个方面的原因,四极质谱领域仍然处于一个快速发展的阶段,有很多问题需要进一步开展研究:1) 随着近年来四极质谱应用领域的快速发展,特别是生命科学、材料科学、环境科学、食品卫生等领域的发展与进步,对质谱仪器的要求也越来越高,如高通量、高灵敏度、快速在线检测等,这些都要求四极质谱领域不仅需要不断研发出新的实验方法和新技术,还要开发出功能更强大、性能更优良、使用更方便,甚至是价格更便宜的四极质谱仪;2) 由于质谱学本身理论的不完备,如四极质谱理论中的高阶场的产生、各种高阶场成分对离子运动的影响、众多离子之间的相互作用在纯四极场和含高阶场情况下的区别以及高阶场对质量分辨能力、离子传输效率的影响等,这都要求四极质谱领域的研究者们继续开展深入的理论和实验研究;3) 其他形状的四极电极系统的性质与作用,如非直线形四极杆电极系统的性质与应用,截面为多边形的四极杆电极系统的性质与应用等。总之,科学技术的不断发展和进步不仅为质谱学的发展和进步提供了很多有利的条件,也对质谱学领域提出了很多新的要求,这些新要求和有利条件是促进质谱学发展的强大动力。 [1] PAUL W, RAETHER H P, von ZAHN U. Das elektrische massenfilter als massenspektrometer und isotopentrenner[J]. Zeit Schrift Fur Puysik, 1958, 152(2): 143-182. [2] BRUBAKER W M. Improved quadrupole mass filter[J]. Journal of Vacuum Science & Technology,1966, 3(5): 305. [3] DU Z, DOUGLAS D J, KONENKOV N. Peak splitting with a quadrupole mass filter operated in the second stability region[J]. Journal of the American Society for Mass Spectrometry, 1999, 10(11): 1 262-1 270. [4] DING L, SUDAKOV M, KUMASHIRO S. A simulation study of the digital ion trap mass spectrometer[J]. International Journal of Mass Spectrometry, 2002, 221(2): 117-138. [5] WANG L, XU F X, DING C F. Performance and geometry optimization of the ceramic-based rectilinear ion trap[J]. Rapid Communications in Mass Spectrometry, 2012, 26(17): 2 068-2 074. [6] SONG Q Y, KOTHARI S, SENKO M A, et al. Rectilinear ion trap mass spectrometer with atmospheric pressure interface and electrospray ionization source[J]. Anal Chem, 2006, 78(3): 718-725. [7] DOUGLAS D J. Linear Quadrupoles in mass spectrometry[J]. Mass Spectrometry Reviews, 2009, 28(6): 937-960. [8] DAWSON, PETER H. Quadrupole mass spectrometry and its applications[M]. Amsterdam: Elsivier Scientific Publishing Compay, 1976: 1-151. [9] DOUGLAS D J, FRENCH J B. Collisional focusing effects in radio frequency quadrupoles[J]. Journal of the American Society for Mass Spectrometry, 1992, 3(4): 398-408. [10] WELLS J M, MCLUCKEY S A. Collision-induced dissociation (CID) of peptides and proteins[J]. Biological Mass Spectrometry, 2005, 402: 148-185 [11] DU Z, DOUGLAS D J. A novel tandem quadrupole mass analyzer[J]. Journal of the American Society for Mass Spectrometry, 1999, 10(11): 1 053-1 066. [12] AUSTIN W E, LECK J H, BATEY J H. Study of the performance of a group of quadrupole mass spectrometry[J]. Journal of Vacuum Science & Technology A-Vacuum Surfaces and Films, 1992, 10(6):3 563-3 567. [13] KONENKOV N. Influence of fringing fields on the acceptance of a quadrupole mass filter operated in the separation mode of the intermediate stability region[J]. Int J Mass Spectrom Ion Proc, 1993, 123(2): 101-105. [14] DENISON D R. Operating parameters of a quadrupole in a grounded cylindrical housing[J]. Journal of Vacuum Science & Technology, 1971, 8(1): 266-269. [15] LOURIS J N, COOKS R G, SYKA J E P, et al. Instrumentation, applications and energy deposition in quadrupole ion-trap tandem mass-spectrometry[J]. Analytical Chemistry, 1987, 59(13): 1 677-1 685. [16] MCLUCKEY S A. Principles of collisional activation in analytical mass spectrometry[J]. Journal of the American Society for Mass Spectrometry, 1992, 3(6): 599-614. [17] DENG L, KITOVA E N, KLASSEN J S. Mapping protein-ligand interactions in the gas phase using a functional group replacement strategy. Comparison of CID and BIRD activation methods[J]. Journal of the American Society for Mass Spectrometry, 2013, 24(5): 988-996. [18] LONDRY F A, WELLS G J, MARCH R E. Enhanced mass resolution in a quadrupole ion trap[J]. Rapid Communications in Mass Spectrometry, 1993, 7(1): 43-45. [19] STEPHENSON J L, BOOTH M M, SHALOSKY J A, et al. Infrared multiple-photon dissociation in the quadrupole-ion-trap via a multipass optical arrangement[J]. Journal of the American Society for Mass Spectrometry, 1994, 5(10): 886-893. [20] DING C, KONENKOV N, DOUGLAS D J. Quadrupole mass filters with octopole fields[J]. Rapid Communications in Mass Spectrometry, 2003, 17(22): 2 495-2 502. [21] DOUGLAS D J, GLEBOVA T A, KONENKOV N V, et al. Spatial harmonics of the field in a quadrupole mass filter with circular electrodes[J]. Technical Physics, 1999, 44(10): 1 215-1 219. [22] KONENKOV N V, SUDAKOV M, DOUGLAS D J. Matrix methods for the calculation of stability diagrams in quadrupole mass spectrometry[J]. Journal of the American Society for Mass Spectrometry, 2002, 13(6): 597-613. [23] DAYTON I E, SHOEMAKER F C, MOZLEY R F. The measurement of two-dimensional fields. Part II: study of a quadrupole magnet[J]. Review of Scientific Instruments, 1954, 25(5): 485-489. [24] LEE-WHITING G E, YAMAZAKI L. Semi-analytical calculations for circular quadrupoles[J]. Nuclear Instruments and Methods, 1971, 94(2): 319-332. [25] REUBEN A J, RADCHIK A V, SMITH G B, et al. Exact fields in multi-electrode ion optics[J]. Rapid Communications in Mass Spectrometry, 1994, 8(12): 939-941. [26] SCHULTE J, SHEVCHENKO P V, RADCHIK A V. Nonlinear field effects in quadrupole mass filters[J]. Review of Scientific Instruments, 1999, 70(9): 3 566-3 571. [27] GIBSON J R, TAYLOR S. Prediction of quadrupole mass filter performance for hyperbolic and circular cross section electrodes[J]. Rapid Communications in Mass Spectrometry, 2000, 14(18): 1 669-1 673. [28] GIBSON J R, TAYLOR S. Numerical investigation of the effect of electrode size on the behaviour of quadrupole mass filters[J]. Rapid Communications in Mass Spectrometry, 2001, 15(20): 1 960-1 964. [29] KONENKOV N, LONDRY F, DING C F, et al. Linear quadrupoles with added hexapole fields[J]. Journal of the American Society for Mass Spectrometry, 2006, 17(8): 1 063-1 073. [30] ZHAO X Z, Xiao Z L, Douglas D J. Overcoming field imperfections of quadrupole mass filters with mass analysis in islands of stability[J]. Anal Chem, 2009, 81(14): 5 806-5 811. [31] SUDAKOV M, DOUGLAS D J. Linear quadrupoles with added octopole fields[J]. Rapid Communications in Mass Spectrometry, 2003, 17(20): 2 290-2 294. [32] KONENKOV N, ZHAO X Z, XIAO Z, et al. Mass analysis in islands of stability with linear quadrupoles with added octopole fields[J]. Journal of the American Society for Mass Spectrometry, 2007, 18(5): 826-834. [33] MORADIAN A, DOUGLAS D J. Mass selective axial ion ejection from linear quadrupoles with added octopole fields[J]. Journal of the American Society for Mass Spectrometry, 2008, 19(2): 270-280.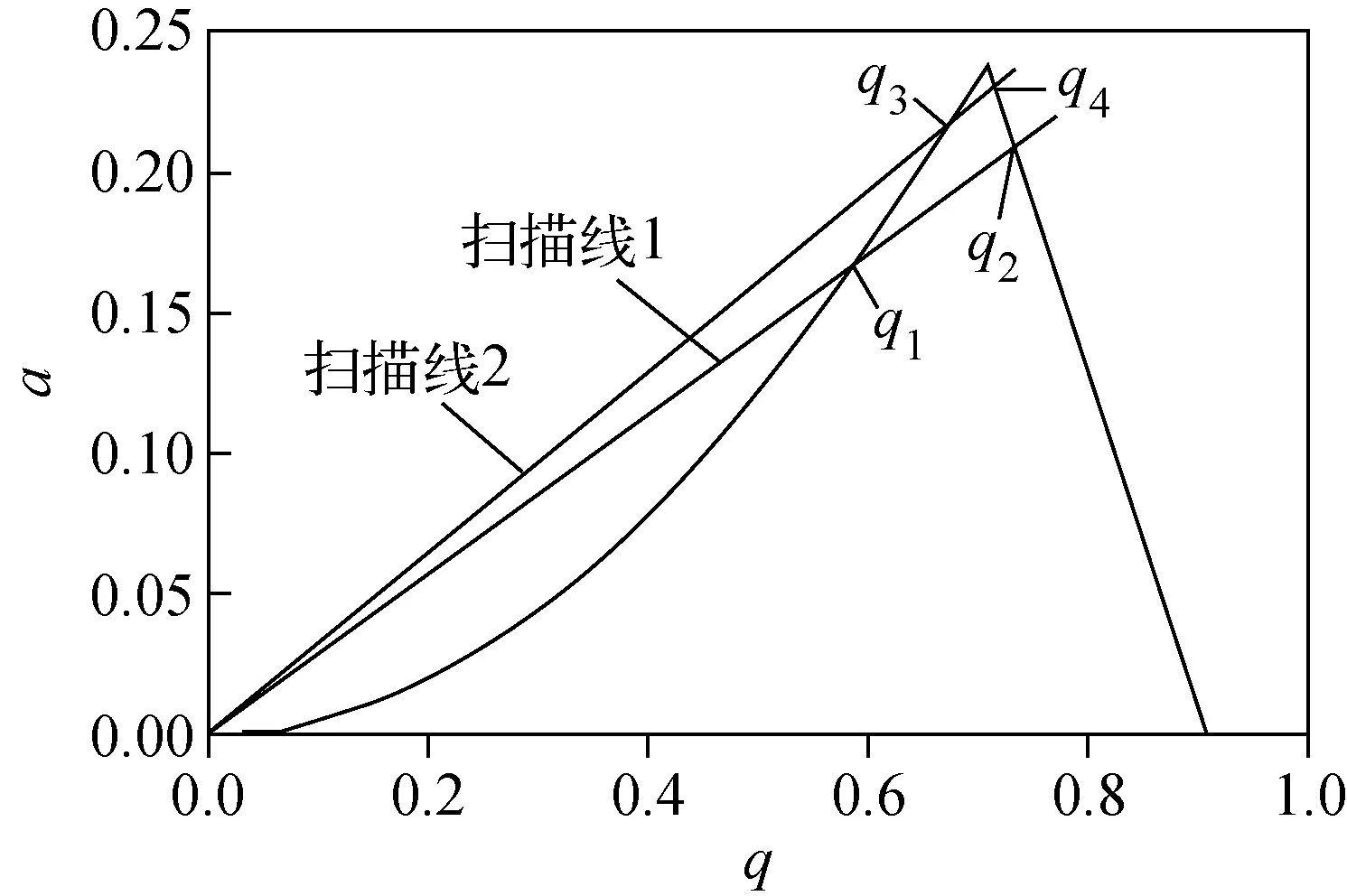
2 四极杆电极系统的应用与性质
2.1 四极杆质量分析器
2.2 四极杆离子导引
2.3 四极线性离子阱质量分析器
3 圆柱形电极组成的四极杆电极系统的研究与开发
3.1 电极半径与电场半径的选择
3.2 高极场效应对四极质谱性能的影响
4 四极杆电极系统的研究前景

