大倾斜角度下基于冷原子重力仪的绝对重力测量∗

吴彬 程冰 付志杰 朱栋 周寅 翁堪兴 王肖隆 林强†

1)(浙江工业大学理学院光学与光电子研究中心,杭州 310023)

2)(浙江大学物理学系光学研究所,杭州 310027)

(2018年6月8日收到；2018年7月20日收到修改稿)

1 引 言

重力场是反映地球物质密度分布的重要基本物理场,高精度的重力场测量在地球物理、资源勘探、惯性导航以及基础物理等领域均具有极其重要的意义和广阔的应用前景.冷原子绝对重力仪[1]是近年来快速发展起来的一种新型的高精度重力测量仪器,它利用原子作为测试质量,并基于冷原子物质波干涉的方法实现精密的重力加速度测量.其原理是通过三束拉曼激光脉冲对原子波包进行分束、偏转以及合束,从而实现冷原子物质波的干涉；重力加速度会改变原子的下落路径,因此会引起干涉路径的相位移动.通过测量冷原子干涉仪的相移可以精确提取重力场信息.与经典的光学干涉式绝对重力仪FG5[2,3](目前最好的商用绝对重力仪)相比,冷原子干涉式绝对重力仪测量重复率更高、灵敏度更高、稳定性更强、可操作性更强、维护更容易且可进行长期连续不间断测量,因此冷原子绝对重力仪有望成为新一代的绝对重力测量仪器.

冷原子重力仪在双光子受激拉曼跃迁[4]成功实现后得以快速发展,斯坦福大学的朱棣文研究小组[1]在实验上首次利用拉曼脉冲实现了冷原子物质波干涉,并测量了重力加速度.随后,他们改进了其实验装置,系统地开展了冷原子重力仪的噪声源和系统误差源研究,使得冷原子重力仪的灵敏度达到20µGal/(1 µGal=10−8m/s2)[5].此外,通过与绝对重力仪FG5进行重力比对,他们发现两套仪器的绝对重力测量精度基本符合,差异为(7±7)µGal.冷原子重力仪实验室样机表现出的高灵敏度和高精度让人们看到了它的巨大潜力,国内外多个研究组相继开展了冷原子重力仪的相关研究[6−16].随着冷原子物理与技术的快速发展,冷原子绝对重力仪逐渐从实验室样机转向工程样机和商用化仪器,其小型化、工程化以及可移动性得到较大改善[17−27].得益于冷原子技术的进步,近些年可移动冷原子绝对重力仪逐渐开始参与绝对重力比对[28−32],其精度和灵敏度得到进一步的检验.最近的比对结果表明冷原子绝对重力仪的灵敏度比FG5稍高一些[31,32],最高可达4.2µGal/[33]；精度稍差于FG5,约4—6µGal[31,32].要成为一种可靠的绝对重力仪计量仪器,冷原子绝对重力仪的性能仍需要进一步研究和改进.

冷原子重力仪的倾斜角会对绝对重力测量产生显著的影响,因此一直是人们关注的热点问题.在冷原子重力仪的实验中,两束拉曼光的波矢方向要求严格重合,且与重力方向(垂线)相平行；因而,冷原子重力仪角度的控制可以改善重力测量的精度.早期的冷原子重力仪实验装置[5]通常都需要一套非常复杂的倾斜控制系统,这些实验室系统体积庞大、结构精细、调节复杂.随后,针对喷泉式原子重力仪,实验装置顶部的拉曼反射镜的倾斜控制得到简化,重力测量灵敏度提高至8µGal/但系统仍旧比较复杂.对于自由下落式冷原子重力仪,倾斜需要先通过水面将拉曼光准直头粗调至垂线方向,再通过调整拉曼反射镜实现两束拉曼光的重合.通过倾斜的调制实验精确找到垂线方向,并利用高精度倾斜计后期数据处理补偿倾斜引起的重力值变化.为了减小振动噪声,针对拉曼后向反射镜的主被动振动隔离技术近年得到快速发展[11,13,33−35],冷原子重力仪的灵敏度也因此得到极大提升[32,33],但是这些隔离系统通常比较复杂,调整时间长、调整步骤繁琐、受外界振动干扰影响较大.为了进一步推动冷原子重力仪的可搬移测量,利用小型化振动隔离平台来被动隔离拉曼反射镜的振动成为一种有效的方法[12,14],这样的隔振装置比较简单,调整方便,使用效率高；然而,该隔振平台的倾斜漂移会影响绝对重力测量.

本文首先从理论上分析了四种不同情况下倾斜对绝对重力测量的影响规律,并基于自行研制的小型化冷原子重力仪,对分析的理论进行了实验验证,实验结果与理论预测相符合.基于此,我们设计了一种基于双倾斜计的绝对重力测量方案,主要是为了解决恶劣测量环境下的冷原子重力仪倾斜漂移问题.此方案利用高精度倾斜计记录放置在被动隔振平台上的拉曼反射镜的倾斜角度,并使用另外一个倾斜计监控真空系统的倾斜,以实现振动噪声的抑制和倾斜的测量.最后,基于自行研制的小型化冷原子重力仪,对该方案进行了实验验证,并最终实现了车间复杂环境下的高精度绝对重力测量.由于振动噪声得到√抑制,冷原子重力仪的测量灵敏度达到319µGal/由于倾斜得到精确测量和补偿,冷原子重力仪的测量精度达到了12.3µGal.本文的实验结果为冷原子重力仪的实用化提供了参考数据.

2 冷原子绝对重力仪原理及实验装置

2.1 冷原子绝对重力仪原理

冷原子绝对重力仪的基本原理是基于受激拉曼脉冲的原子物质波干涉,文献[5]中有详细的描述.下面进行简要说明.在超高真空腔中,通过激光冷却技术首先制备一团低温的87Rb原子团,经过偏振梯度冷却进一步降低原子团的温度.通过关掉磁场和光场使原子在重力场中自由下落,利用微波脉冲实现原子态的纯化,随后利用双光子受激拉曼跃迁[4]来实现原子态的操控和选择,以制备一团对磁场不敏感且温度更低的原子团(原子处于52S1/2,F=2,mF=0态上).然后,通过作用三束拉曼脉冲π/2-π-π/2实现原子物质波的分束、偏转以及合束,最终实现一个马赫-曾德尔原子干涉仪.最后,在探测区通过时间飞行法分别探测原子的荧光信号,得到原子在两个态上的布居数,并通过归一化减小原子涨落对测量的影响.归一化的原子布居数P可以表示为

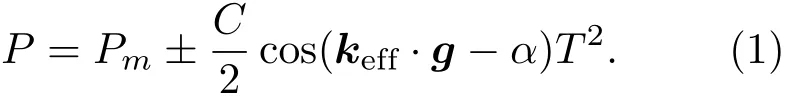
其中,Pm是平均的归一化原子布居数；C是干涉条纹对比度；kfi=k1−k2是拉曼光束的有效波矢,k1和k2分别是两束拉曼光的波矢；g是重力加速度；α是用于补偿重力诱导的多普勒频移的拉曼光扫频啁啾率；T是两束拉曼脉冲之间的时间间隔.

针对 (1)式,如果α0=kfi.g,则无论如何改变T,原子布居数总是一个极值.反之,如果扫描不同T下的干涉条纹,所有条纹会交于同一个α0点,也就是所谓的暗条纹点,这时绝对重力值g0=α0/kfi(拉曼光波矢与重力方向平行).

2.2 冷原子绝对重力仪实验装置

小型化冷原子绝对重力仪实验装置如图1所示,主要包含三个部分:超高真空系统、激光光路系统和电子控制系统.

1)超高真空系统

本文所用的超高真空系统是之前实验装置[14]的改进版,它包括超高真空核心腔、磁场系统、外围光学系统、微波天线、荧光收集系统、双层地磁场屏蔽系统等.与之前自由下落式金属真空腔不同,我们基于石英玻璃材料自主研制了一套全新的小型化真空腔,真空腔体主要包括二维磁光阱、三维磁光阱、干涉区、探测区等部分,这些部分全由玻璃材料构成,通光的面积大大增加,以至于整个真空腔体积被大大缩减,核心玻璃真空腔的高度约20 cm.整个真空腔的真空度靠一个20 L/s的离子泵维持.核心玻璃真空腔被安装在一块铝板上,周围缠绕了磁场线圈,搭建了准直头及分光光路,安置了微波天线和荧光收集透镜组；此外,铝板上安装了一个高精度的倾斜计,用于记录真空系统的倾斜角度；铝板的外围是两层坡莫合金,主要用于磁场屏蔽；磁屏蔽放置在一个可调整角度的支撑结构上,通过底部的三个脚可精细调节真空系统的倾斜值.铝板和磁屏蔽底部开有一个直径为50 cm的通孔,用于拉曼光出射,拉曼后向反射镜放置在一个商用的被动振动隔离平台上,以隔离地面振动噪声的影响.被动平台上放置了第二个相同型号的倾斜计,可实时记录拉曼反射镜的倾斜角度.真空系统和拉曼反射镜是分离的,可分别进行倾斜调节.整个真空系统直径是0.6 m,高度约1 m,重量约70 kg,实物图如图1(a)所示,该真空系统具有紧凑、小型化和可搬移的特点.

2)激光光路系统

冷原子绝对重力仪的光路方案与文献[36]相似,共用到两个外腔式半导体激光器(ECDL)和两个激光放大器,所有冷原子重力仪所需的激光频率都通过这两个种子激光器实现,包括冷却光、再抽运光、探测光/吹F=2态光、吹F=1态光以及拉曼光.激光放大器使不同频率光的功率满足不同实验过程所需,包括二维磁光阱、三维磁光阱、原子干涉以及归一化探测.大致方案如下,首先利用频率调制谱(FMS)将一半导体激光器的频率锁定在87Rb原子D2线的F=1→F′=1共振跃迁上,这个光可以作为再抽运光,通过声光调制晶体(AOM)移频可以产生吹F=1态光.另外一个激光器的频率通过光学锁相的方法进行锁定,且在不同实验阶段可以进行改变,这个光可作为冷却光,通过AOM移频可以产生吹F=2态光.两个激光器的光束合束后,利用双通道AOM方案,实现大失谐400 MHz的拉曼光,这时两台激光器分别可以作为拉曼F=1和拉曼F=2的光.最后,利用单模保偏光纤将冷原子重力仪所需的激光输送给超高真空系统,整个光路系统搭建在一个定制的光学平板上,激光光路实物图如图1(b)所示.该冷原子重力仪激光方案具有激光器用量少、激光光路简单、激光功率利用率高等特点,因此比较适合于小型化冷原子重力仪.

3)电子控制系统

如图1(c)所示,所有电子电路系统、数据采集系统、时序控制系统、供电系统都集成在一个定制的标准19寸机柜中.电子电路系统主要包括激光器控制器、AOM驱动器、电光调制器驱动器、机械快门驱动、C场电流源驱动、二维及三维磁光阱磁场驱动、地磁场补偿驱动和频率链等.大部分电路自主模块化设计,集成到三个标准的19寸电路盒中,电路柜前后有盖板,并安装有风扇以实现电子控制系统的散热.电子控制系统通过电缆与激光光路系统连接,服务于光路控制；通过一根多芯线与超高真空相连接,实现信号的输入输出.

图1 小型化冷原子绝对重力仪实验装置图 (a)超高真空系统；(b)激光光路系统；(c)电子控制系统Fig.1. The experimental apparatus of the miniaturized cold atom absolute gravimeter:(a)Vacuum chamber；(b)laser and optical path system；(c)electronic and control system.

2.3 冷原子绝对重力仪实验步骤

本文中的冷原子绝对重力仪实验步骤与大多数自由下落式原子重力仪类似[14,35],通常包含四个步骤:冷原子团制备、量子态纯化、三脉冲原子干涉序列、归一化态探测.首先,利用二维磁光阱(2D-MOT)制备一束扁平的冷原子团(87Rb原子)；在水平方向上,通过二维的推送光将这团冷原子束输送到三维磁光阱(3D-MOT).二维磁光阱与三维磁光阱之间有一个差分管以维持两边的真空压差,利用二维磁光阱可提高三维磁光阱的装载率,还能保持原子干涉区有较高的真空度.300 ms时间内,三维磁光阱可装载大约108个原子.其次,将所有磁场关断,通过降低冷却光失谐和功率(偏振梯度冷却阶段),进一步冷却原子团温度至6µK.在光场彻底关断以后,冷原子团在重力场作用下自由下落,这时在竖直方向上作用一个50 mG的磁场用来定义量子化轴.通过作用微波和拉曼选态π脉冲,将原子制备到对磁场不敏感的|F=1,mF=0⟩纯态上,其他磁子能级原子都被共振光吹掉.紧接着,开始作用三束多普勒敏感的π/2-π-π/2拉曼脉冲序列使得原子波包干涉(马赫-曾德尔干涉仪).拉曼π脉冲时间为12µs,拉曼脉冲之间时间间隔T为60 ms.最后利用归一化探测系统收集原子荧光信号,实现原子布居数的归一化探测.目前,该小型化原子重力仪整个测量周期耗时0.5 s,测量重复率为2 Hz,包括原子装载、选态、干涉以及探测.

3 倾斜对绝对重力测量的影响分析

倾斜对绝对重力测量的影响是显著的.在原子重力仪实验中,如果拉曼光波矢方向与重力方向不重合,则测量到的是重力加速度的分量,值会变小；比如拉曼光方向与重力垂线方向夹角1 mrad,则重力值减小可达上百甚至上千微伽,远远高于其他系统误差；因此在进行绝对重力测量前,必须仔细考虑倾斜对测量的影响.

由(1)式可知,倾斜引起的原子干涉仪相移∆Φ可以写为:

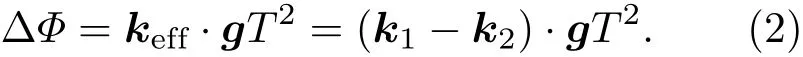
考虑到拉曼光波矢方向与重力方向的重合情况,一般把倾斜对重力的影响分为四种情况,如图2所示.

1)两束拉曼光k1,k2重合,且与重力方向重合

如图2(a)所示,k1,k2分别与重力方向重合,k1与重力方向夹角为0,k2与重力方向夹角为π,则(2)式可写为

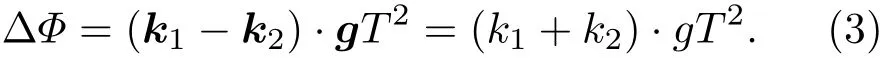
这种是理想情况,测量的绝对重力值最大.

2)两束拉曼光k1,k2重合,且k1与重力方向夹角为θ

如图2(b)所示,k1,k2的方向重合,k1与重力方向夹角为θ,k2与重力方向夹角为(π−θ),这种情况下,(2)式可写为一般θ比较小,可将cosθ泰勒展开且忽略高阶项,得到

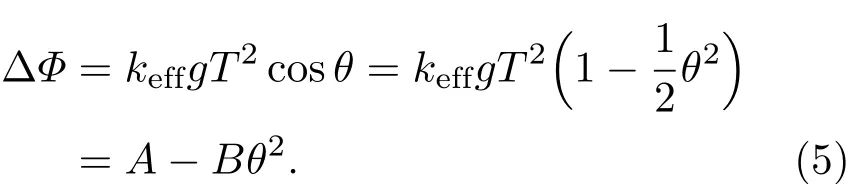
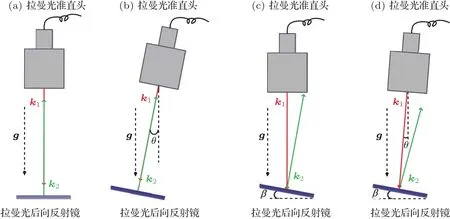
图2 倾斜对绝对重力测量的影响示意图Fig.2.The schematic diagram of the absolute gravity measurement affected by systematic tilt.

进一步,由倾斜引起的重力值相对变化可以写为

由(5)式可知,原子干涉仪的相移(重力值)随倾斜角度的变化呈抛物线关系,抛物线开口向下(−B),顶点值A处重力值最大,也是拉曼光波矢方向与重力方向重合的点.在抛物线顶点位置附近,重力值对倾斜的变化不太敏感,因此冷原子绝对重力仪一般工作在抛物线顶点位置.这种情况多适用于将整个冷原子重力仪放置在一个被动隔振平台上,θ为整个实验装置的倾斜角.

3)两束拉曼光k1,k2不重合,且k1与重力方向重合,拉曼反射镜倾角为β

如图2(c)所示,k1与重力方向夹角为0；拉曼后向反射镜与水平方向夹角为β,由几何关系知k2与重力方向的夹角为2β,则(2)式可表示为

考虑到实际实验中,kfi≈2k1≈2k2,则上式可化简为

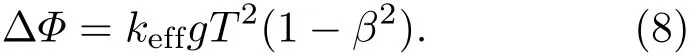
则由倾斜引起的重力值相对变化可以写为

这种情况尤其适用于装置固定在地面上,拉曼反射镜放置在被动隔振平台上.因被动隔振平台的倾斜漂移比较大,β的变化就会引起重力值变化.与第二种情况类似,原子干涉仪的相移(重力值)随倾斜角β的变化呈抛物线关系,抛物线开口向下,顶点值处重力值最大,也是拉曼光波矢方向与重力方向重合的点.不同的地方是此抛物线开口的程度比第二种情况大一倍,比较(5)和 (8)式即可得出.针对图2(b)和图2(c)的情况,理论模拟的倾斜引起的重力值变化如图3所示,两个抛物线的开口分别是−A和−2A.

4)两束拉曼光k1,k2不重合,且k1与重力方向夹角为θ,拉曼反射镜倾角为β

如图2(d)所示,k1与重力方向夹角为θ,拉曼反射镜倾角为β,由几何关系可得出k2与重力方向夹角为π−(2β−θ),则(2)式可写为

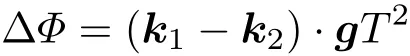
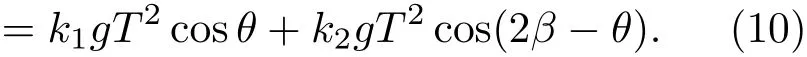
考虑到kfi≈2k1≈2k2,则上式可化简为

这种情况适用于大振动情况,或者测量放置平台不稳,且拉曼反射镜放置在被动隔振平台上,整个装置的倾斜角和拉曼反射镜的倾斜角都随时间变化.针对这种情况,需要用(11)式对测量到的重力值进行修正,两个角度分别会引起一个抛物线曲线,且有一个交叉项.

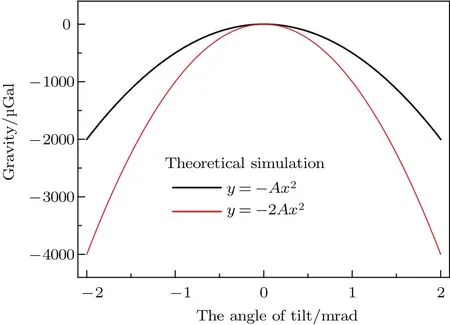
图3 倾斜引起的重力值变化理论模拟 黑线对应图2(b)情况；红线对应图2(c)情况Fig.3.The theoretical simulation of the gravity relative change caused by systematic tilt. The black and red curve correspond to the case of Fig.2(b)and Fig.2(c)respectively.

4 基于双倾斜计的绝对重力测量

4.1 基于双倾斜计的绝对重力测量方案介绍

如图1所示,利用一个紧凑的自由下落式冷原子重力仪开展绝对重力测量任务,采用的是双倾斜计测量方案,其中一个高精度二维倾斜计固定在真空系统底板上,真空系统的角度可通过底部的三个调整脚快速调节；另外一个倾斜计放置在一个小尺寸的被动隔振平台上,平台上放置了拉曼光后向反射镜,拉曼反射镜角度可通过小配重块进行调节.两个倾斜计是同一个型号,能够实时输出X和Y方向的倾斜值,分辨率达到0.1µrad.采用拉曼反射镜和真空系统分离的双倾斜计方案,主要是为了隔离大振动噪声,且能够进行快速的绝对重力测量.在先前的冷原子重力仪实验中,不论是将整个冷原子重力仪放置在大隔振平台上[8],还是对拉曼反射镜进行主被动联合隔振[13]；一般系统都比较庞大且复杂,调整难度大且耗时较长,这些方案不适合在恶劣环境下进行快速绝对重力测量.针对我们小型化重力仪的可快速搬移特点,采用双倾斜计方案是一个很好的选择.

4.2 绝对重力测量实验的环境数据介绍

本次测量是在城市闹区的一个车间内开展,车间旁有大型设备需要一直运行,振动环境较差.利用微振仪测量到的地面振动的速度信号如图4(a)所示,振动速度峰峰值约为80µm/s；分析此信号得到的地面振动加速度的功率谱密度如图4(b)所示,在3—10 Hz频段,振动加速度幅度可达10−4m/s2,因此测量点的振动环境不是很理想.测量房间的温度通过空调控制,变化幅度约6◦C/每晚,温度变化周期受空调性能影响,一个周期约30 min,湿度变化约15%/每晚.需要进行重力测量的点有三个,分布在两个房间,其中一个房间的测量点之前用FG-5测量过,绝对重力值已知,需要再次检验；另外两个测量点在另一个房间,相距约5 m.每个测点的测量时间约12 h(一般晚八点到早八点).

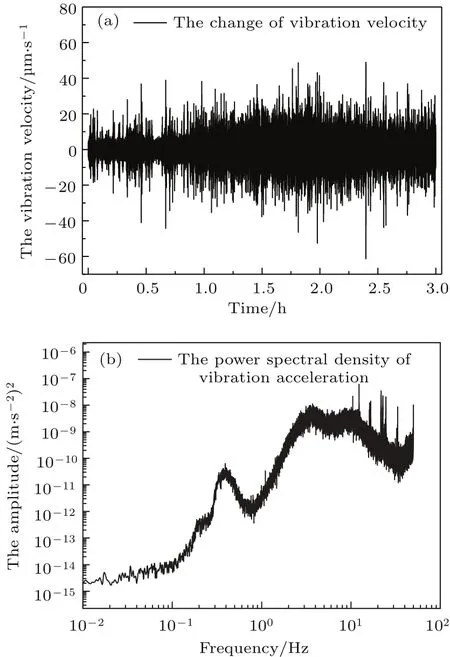
图4 测试点地面振动速度随时间的变化曲线及振动加速度的功率谱密度(PSD)分析 (a)测量到的地面振动速度随时间的变化；(b)分析得到的地面振动加速度的PSDFig.4.The ground vibration velocity measured at the comparison site and the obtained power spectral density of vibration acceleration:(a)The recorded change of ground vibration velocity as a function of time；(b)the power spectral density(PSD)of vibration acceleration deduced from the measured vibration velocity.

4.3 绝对重力测量实验中倾斜的测量调整及处理校正

考虑到测量环境的特殊性,尤其是重力仪放置平台的倾斜会随时间变化,倾斜角度可以利用倾斜计1实时测量.而且,被动隔振平台的倾斜也会随时间变化,倾斜角度可以利用倾斜计2实时测量.下面介绍利用双倾斜计方案如何实现倾斜的测量调整和后期数据处理补偿,一般分三个步骤进行.

1)垂线调整

首先在一个振动噪声较小的环境下,结合高精度水平仪,调整图1(a)真空装置底部的三个支撑脚实现倾斜粗调整.然后,在真空系统下底板放置水面,利用小光阑对光的方法粗调拉曼光准直头至大致的垂线方向.随后,拿掉水面在同一位置放置拉曼后向反射镜,利用小光阑对光的方法粗调拉曼返回光与入射光的重合.这种情况可将拉曼反射镜和真空系统看作一个整体,倾斜计可以记录整体的倾斜角度.与文献[13]类似,我们在拉曼光入射准直头前放置功率监控点,通过细调拉曼反射镜角度,可以让拉曼返回光原路进入光纤,且被光纤后的功率探头测量到,通过这种方法可以实现两束拉曼光的严格重合.最后,通过小角度依次改变X方向和Y方向的倾斜进行倾斜调制实验以找到垂线方向,类似于图2(b)的情况.

测量的倾斜引起的重力值变化如图5所示,对应tiltmeter 1测量结果,黑点是测量的实验数据,红线是抛物线拟合的曲线,拟合函数为y=y0−A(x−x0)2,拟合系数A约为500.图5(a)和图5(b)分别是X和Y两个方向的测量结果,垂线方向可以用拟合抛物线零点的倾斜坐标值表示(θtx10,θty10).

2)两束拉曼光重合调整

在步骤1确定真空系统的垂向后,将冷原子重力仪移到测试房间,进行下一步的调节.首先,将真空系统放置在测量点的正上方,通过调整底部的三个支撑脚将其调到垂向方向(倾斜计1的示数是(θtx10,θty10)).然后,将拉曼后向反射镜从真空系统中拆下,并安置在一个商用的被动振动隔离平台上,以隔离地面的随机振动噪声.为了减小被动隔振平台的倾斜漂移,在其上部放置了自制的配重平板和配重块,配重块主要用于抵消倾斜计的重量,且进行小角度倾斜调制实验.随后,通过调整拉曼光后向反射镜的调整架以改变拉曼返回光的倾斜,通过光纤后的拉曼返回光监控点确定两束拉曼光的重合.最后利用小配重块分别进行X和Y方向的倾斜调制实验,这种情况与图2(c)类似,拉曼反射镜倾斜角度对原子干涉仪相移的影响可由(8)式给出.实验测量的抛物线数据如图5所示,对应图中的tiltmeter 2测量结果,图5(a)和图5(b)分别是X和Y两个方向的测量结果,绿点是测量的实验数据,蓝线抛物线拟合的曲线,用同样的拟合函数得到的系数A约为1000,比图2(b)情况下的值大一倍,实验结果与图3的理论模拟相符合.此时,拉曼光严格重合,可以用拟合的抛物线零点的倾斜坐标值(θtx20,θty20)表示.

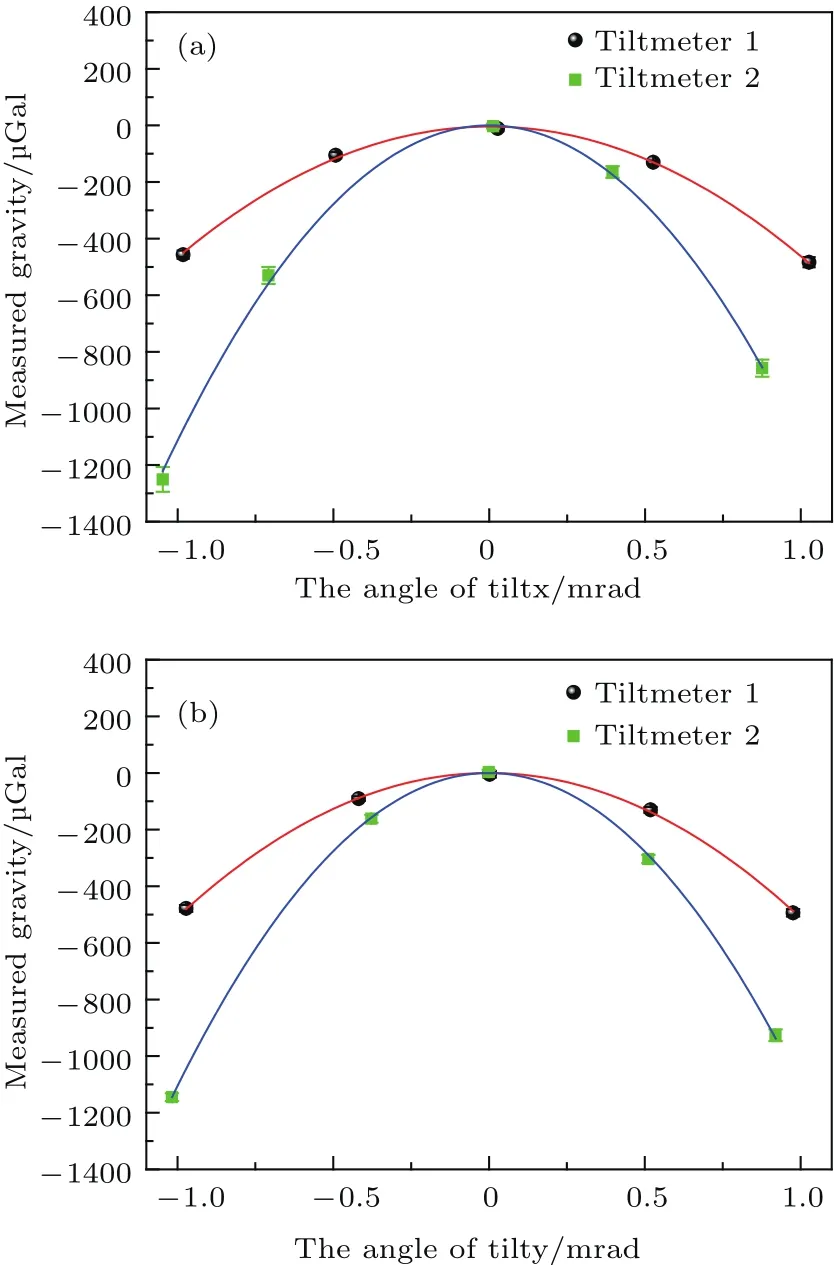
图5 利用倾斜调制实验以调整系统倾斜 (a)X方向重力值随倾斜角度的变化曲线；(b)Y方向重力值随倾斜角度的变化曲线；黑色点代表倾斜计1的实验数据,绿色点代表倾斜计2的实验数据,红线和蓝线是实验数据的抛物线拟合曲线Fig.5.Adjustment of the system tilt based on the experiment of tilt modulation.(a)The dependence of gravity on the degree of tilt in the X direction；(b)the dependence of gravity on the degree of tilt in the Y direction.The black and green scatter points correspond to the experimental data measured by tiltmeter 1 and tiltmeter 2 respectively；the red and blue curves denote the parabolic fitted curves of the measured experimental data.

3)双倾斜计实时测量及后期数据处理校正

在实际测量中,真空系统和拉曼后向反射镜都会发生倾斜,这就是上述图2(d)分析的情况.鉴于前两个步骤的调整,重力测量系统已处于抛物线顶点位置,即倾斜计1的读数是(θtx10,θty10),倾斜计2的读数是(θtx20,θty20).在这个状态下,倾斜角度的微小变化对重力值的影响幅度不会太大.然而,倾斜随时间漂移以后,倾斜的影响将会逐渐显现.我们利用倾斜计1和2实时记录绝对重力测量过程中的倾斜角度变化,实验数据如图6所示,记录时间长度约15 h.由图可以看出,倾斜计1的测量值变化并不大,X和Y方向的倾斜变化峰峰值约为15µrad.而放置在被动隔振平台上的倾斜计2,其测量值变化较大,X和Y方向变化峰峰值约为100µrad.

为了后期数据处理修正倾斜引起的重力值变化,需要用到(11)式,考虑到倾斜的X和Y两个分量以及两个倾斜计的实时测量数据(θtx1(t),θty1(t)),(θtx2(t),θty2(t)),可以将倾斜计引起的重力修正值g(t)写为

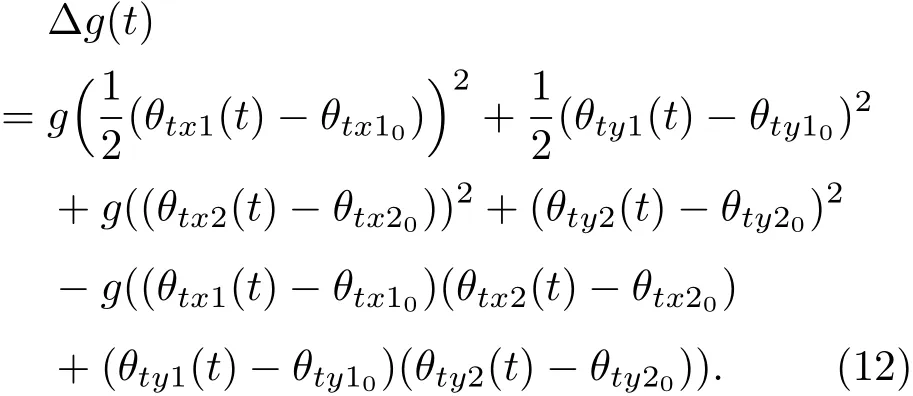
(12)式第一行是由倾斜计1引起的重力变化,第二行是由倾斜计2引起的重力变化,第三行是两个倾斜计交叉项引起的重力值变化.基于图6的实验测量数据,可以分别计算倾斜计1、倾斜计2、交叉耦合等引起的重力值变化,计算结果如图7所示.为了更好地分辨曲线细节,我们对图中数据做了移动平均处理,移动平均的取样数为30,对应单点时间约为15 s.如图7所示,倾斜计1引起的重力值变化幅度较小,在1µGal以内；倾斜计2引起的重力值变化较大,幅度可达15µGal；交叉项的影响也不大,幅度在1µGal以内；最后三项加起来计算的总修正幅度最大值约15µGal.在实际测量中,需要后期数据处理校正倾斜引起的总修正,否则测量到的绝对重力值会偏小.

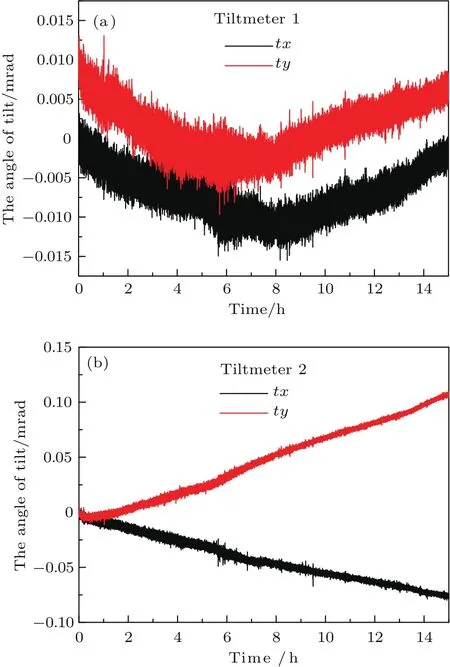
图6 双倾斜计记录的倾斜角度随时间变化数据 (a)和(b)分别是倾斜计1和倾斜计2测量到的倾斜角度随时间的变化曲线；其中黑线和红线分别代表X方向和Y方向的倾斜变化Fig.6.The angle of tilt changes as the measured time,which is recorded by two tiltmeters.(a)and(b)denote the signals measured by tiltmeter 1 and tiltmeter 2；the black and red curve represents the tilt change measured in the X and Y direction.

图7 倾斜引起的重力值变化 黑线、红线、绿线依次是由倾斜计1、倾斜计2、交叉耦合项引起的重力值变化,蓝线是最后合成的总的重力值变化Fig.7. The change of gravity due to the system tilt.The black,red,and green curve represents the gravity change due to the effect of tiltmeter 1,tiltmeter 2,and the crossover item.The blue curve denotes the overall contribution of gravity correction induced by system tilt.

4.4 绝对重力值测量结果

在倾斜调整完后,通过测量不同T的原子干涉条纹可以找到暗条纹点,进而可以开始绝对重力测量.实验中测量了三个标定点,下面我们只对第一个测点的数据进行分析.测量到的潮汐数据如图8(a)所示,测量时长约13 h,利用双倾斜计方案通过后期数据处理补偿了倾斜引起的重力值变化.单点测量时间约57 s,由图8(a)可知,实验数据与潮汐理论数据符合比较好.潮汐理论数据减去实验数据可以得到残差数据,如图8(b)所示,漂移基本在±20µGal.

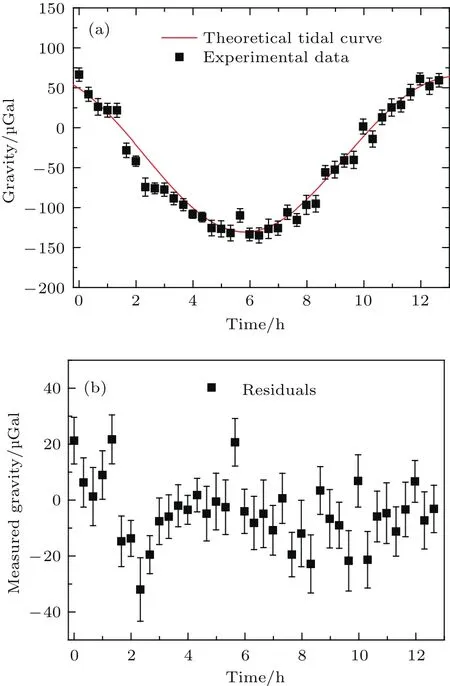
图8 潮汐测量(单点20 min平均)Fig.8.The measurement of tidal data(it takes 20 min for one point).

冷原子重力仪的测量灵敏度反映了仪器的噪声水平.实际测量中,不同重力仪的测量重复率不同,因此单个重力数据的获取时间有差异,单次测量的噪声、分辨率等会有所不同.为了对不同仪器的噪声水平进行比较和评估,通常利用艾伦方差法评估不同重力仪的分辨能力和稳定性,并将艾伦方差曲线上1 s时的重力值作为评估重力测量性能的一个重要指标.不同仪器都可以通过计算其数据的艾伦方差,并归算到1 s,从而使不同仪器的性能可以得到比较.因此,冷原子重力仪的灵敏度也可以理解为1 s时间内仪器能够达到的重力分辨率水平.考虑到冷原子重力仪的噪声(白噪声)随时间有规律(如图9所示),我们评估出的重力测量灵敏度约为319µGal

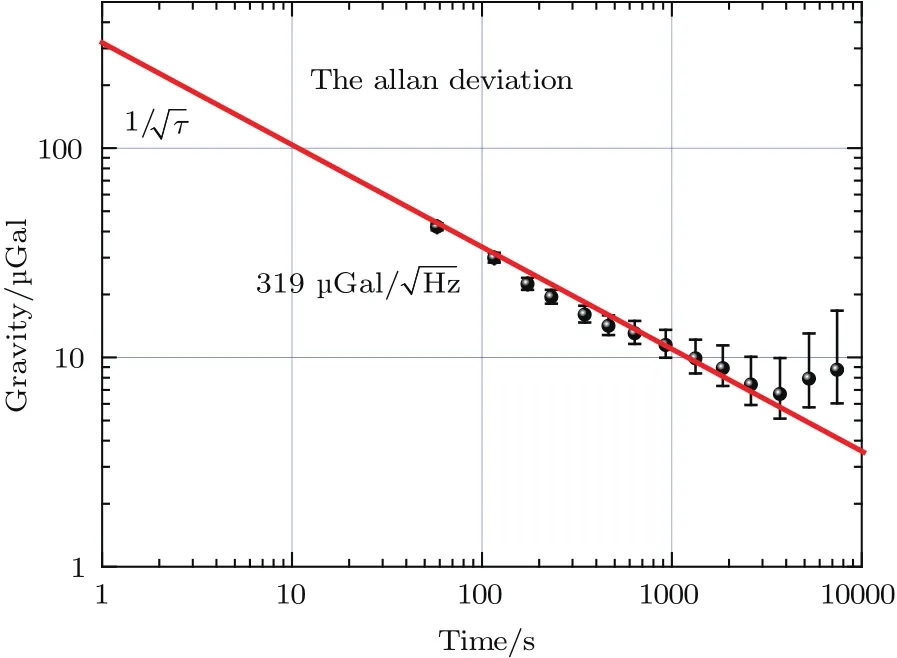
图9 重力测量灵敏度评估Fig.9.The evaluation of the sensitivity of cold atom gravimeter.

冷原子重力仪的灵敏度主要受振动噪声和拉曼光相位噪声影响.从原理上讲,重力数据是从原子干涉条纹中提取的,能影响原子干涉条仪相位抖动的因素都可以看作是仪器的噪声源.冷原子重力仪基本原理可以理解为通过精确测量原子与拉曼光后向反射镜之间的距离h和原子自由下落的时间t,再利用自由落体公式计算重力加速度g.h的测量以物质波波长为基准,t的测量以超稳晶振或原子钟的频率输出为基准.地面振动噪声会影响h的变化,其实冷原子重力仪测量到的加速度包含重力加速度和地面振动加速度,由相对论理论可知,这两者是不可分辨的,因此通过隔振装置减小地面振动噪声可以提高测量灵敏度.拉曼光相位噪声与t的测量有关,因此通过改进拉曼激光锁相环的相位噪声可以提高仪器的灵敏度.

由13 h的残差数据可以评估测量到的重力值平均值,为了得到绝对重力值还需要修正其他系统误差项.对于我们的自由下落式冷原子重力仪,主要的系统效应引起的重力偏置及其不确定度得到评估,冷原子绝对重力仪总修正值约为−165.0µGal,仪器合成不确定度为12.3µGal.

倾斜会引起干涉条纹对比度下降,并引起其他系统效应发生变化.对射拉曼光不重合会使得空间不同位置的光场幅度和相位发生改变,由于不同空间位置的原子感受到的光场不同,相应的拉比振荡频率会发生变化,从而导致原子干涉条纹对比度下降.与此同时,由于不同空间位置的原子感受到的拉曼光波前不同,波前畸变效应引起的系统误差也会发生变化.在我们的实验中,拉曼光光斑直径约为30 mm,原子团自由下落时的尺寸约为1—2 mm,干涉作用时间约为120 ms(T=60 ms),冷原子团温度6µK,因此冷原子团在三个拉曼脉冲作用时感受到的拉曼光变化并不大.经评估,在小角度对射拉曼光不重合的情况下,原子干涉条纹的对比度变化不大；由波前畸变效应引起的系统误差变化并不大,该项系统效应的评估不确定度小于冷原子重力仪总的不确定度,因此我们不做特殊修正.

此外,我们还修正了环境因素引起的重力值变化,包括气压(5.3µGal)、极地运动(4.9µGal),经过修正后可以得到最后的绝对重力值.考虑到仪器高度以及该测点的重力梯度值,我们将重力值修正到地面,并与之前用FG-5在该点测到的值进行了比较,测量值基本符合.

5 结 语

基于一个紧凑且可搬运的冷原子重力仪,本文提出了一种双倾斜计绝对重力测量方案,在车间大倾斜角度情况下成功测量了指定测点的绝对重力值,且该值与先前用FG-5测量的值基本符合.本文从拉曼后向反射镜与真空系统位置出发,理论分析了四种情况下倾斜对绝对重力测量的影响,并在实验中进一步进行了验证,实验结果与理论预测相符合.利用小型被动隔振平台抑制拉曼反射镜的振动,冷原子重力仪的测量灵敏度可达319测量到的重力值随时间变化曲线与潮汐理论曲线相符合.由于倾斜得到精确测量和后期补偿,冷原子重力仪的测量精度达到了12.3µGal.本文在实验上证明了基于双倾斜计进行绝对重力测量方案的可行性,这为未来利用冷原子重力仪提供重力测量服务提供了参考数据,也为复杂环境下进行绝对重力测量提供了思路.