反馈脉冲棘轮的能量转化效率研究∗
延明月 张旭 刘晨昊 黄仁忠 高天附† 郑志刚
1)(沈阳师范大学物理科学与技术学院,沈阳 110034)
2)(华侨大学信息科学与工程学院,厦门 361021)
(2018年5月31日收到;2018年7月11日收到修改稿)
1 引 言
生物分子马达是将化学能转化为机械能的一大类酶蛋白生物分子,在细胞内的物质输运过程中起着非常重要的作用[1].为了深入了解分子马达的动力学机理,人们提出了双温棘轮[2]、反馈控制棘轮[3],hand-over-hand棘轮[4]等大量的布朗棘轮模型[5−8].通过对不同类型棘轮的研究,不仅能深入地理解布朗粒子的定向输运机理,而且还有助于分析生物医学上药物投放等输运过程[9,10].同时,也可为医疗上如何提高药物精准投放及药物的有效利用率等提供理论指导[11−14].
目前,关于棘轮定向输运的研究已引起人们的广泛兴趣[15−18].如Dinis和Quintero[19]建立了过阻尼布朗棘轮模型,研究发现合适的外力振幅可以使粒子的定向输运达到最强.同时,Wang和Bao[20]建立了二维摇摆棘轮,结果表明,耦合粒子间的相互作用与摇摆驱动之间的协同作用能促进粒子的定向输运.此外,Cubero和Renzoni[21]也对欠阻尼棘轮的输运问题进行了讨论,发现一定的驱动相位能够诱导棘轮的流反转.通过对不同类型棘轮的研究,不仅能使人们理解棘轮的定向输运行为,而且对于分析细胞内分子马达拖动负载时的能量转化具有一定的实验启发.
实验研究表明,细胞内大多数的生物分子马达都是拖动负载进行定向步进的酶蛋白生物大分子,其拖动负载做功的效率普遍都非常高,如旋转ATP合成酶.舒咬根等[22]研究发现,野生型驱动马达在一个力学化学耦合循环作用中水解一个ATP,其能量利用率高达70%[23].最新的研究表明,驱动马达只有在小负荷时水解一个ATP并移动一步,而在大负荷时移动一步需要水解多个ATP[24].然而,对于无偏置力和负载作用下布朗粒子的输运效率问题,Nutku和Aydiner[25]的研究结果表明粒子对棘轮系统输入能的利用仅为2‰左右.此外,文献[26]对热机效率进行讨论,发现布朗热机能够达到的最大效率仅为1%左右.通过对比上述实验结果与理论分析发现,棘轮模型的效率与实验上测得的马达效率相比仍有较大差距.因此,如何从理论上提高不同类型马达拖动负载做功时的效率问题至今仍是非常重要的研究课题.此外,Delacruz等[27]的研究表明,大多数的分子马达都是以集体形式向前步进,其每跨一步水解一个ATP.由于马达头部与微管蛋白的结合会使蛋白螺旋分离,从而导致它们的催化周期处于不同的相位上.因此,相位差引起的脉冲作用对于细胞内生物分子马达的定向运动乃至反转都将起至关重要的作用[28].基于这一实验结果,文献[29]建立了相应的反馈棘轮模型,并研究了自由长度等因素对棘轮定向输运的影响.然而对于该耦合马达在细胞环境中拖动负载做功时的能量转化问题,仍不十分清楚.因此,本文在上述研究的基础上进一步分析反馈脉冲棘轮的定向输运,详细讨论耦合粒子的能量转化效率问题.
为了全面了解反馈脉冲棘轮的输运性能,本文研究了耦合马达拖动负载时的定向输运以及能量转化效率.研究发现,处于一定的脉冲相位下,耦合粒子拖动负载的运动方向会发生反转,且存在合适的脉冲相位能使棘轮的定向输运达到最强;一定的耦合强度以及合适的自由长度也能使脉冲棘轮的定向输运达到最强,从而使耦合粒子的能量转化效率达到最大.本文所得结果可为人工纳米器件的优化设计提供新思路,并为实现不同粒子的筛选提供理论基础[30,31].
2 反馈脉冲棘轮
本文主要研究耦合布朗马达拖动负载时的运动情况,同时马达还将受到无偏外力及热噪声的作用,其动力学行为可由无量纲化的过阻尼朗之万方程描述[32,33]:
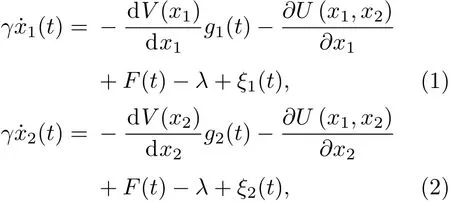
其中t为时间;两个耦合布朗粒子的位置分别为x1(t)和x2(t);γ为介质的阻尼系数;λ为负载;方程为粒子受到棘轮势的作用,V(x)为周期外势表示为
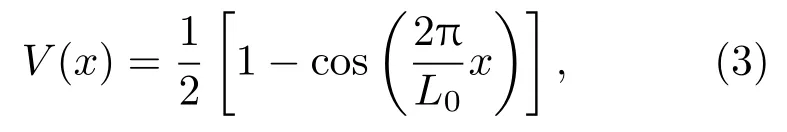
其中L0为棘轮的周期.由于生物体内分子马达在ATP水解过程中受到环境的影响,从而导致耦合马达的催化周期处于不同的相位.因此,理论上我们可采用反馈调制g1,2(t)来表示这一相互作用[29],其具体形式为:

因此,方程(1),(2)表达的是一种反馈脉冲棘轮.此外,U(x1,x2)为两个耦合布朗粒子的相互作用势,具有如下关系:
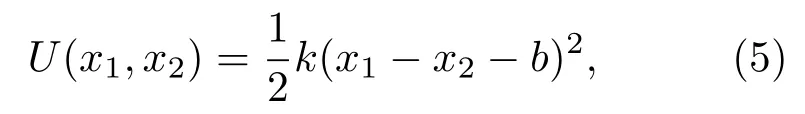
其中k为耦合强度,b为弹簧的自然长度.脉冲棘轮受到的外力F(t),本文采用的是周期外力,其表述为
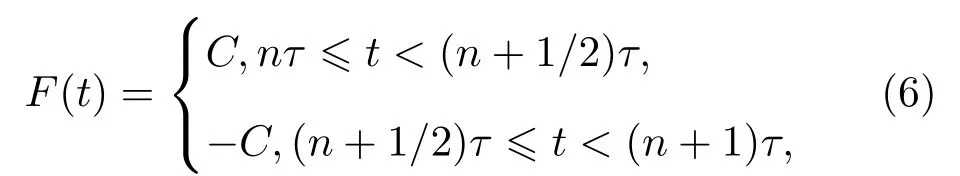
上式中C为周期外力的振幅,τ为外力作用周期.此外,ξ1(t)和ξ2(t)为高斯白噪声,且满足如下统计特征:
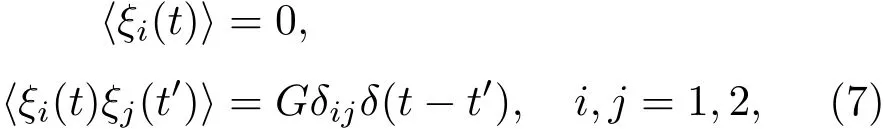
其中G为噪声强度.
为了研究反馈脉冲棘轮的定向输运,本文采用耦合粒子质心的平均速度来描述棘轮的输运情况,表述如下[34]:
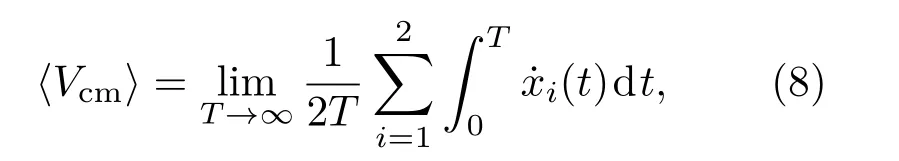
其中,⟨.⟩表示系综平均.由于布朗粒子会产生自由扩散现象,因此利用平均有效扩散系数Dfi来研究耦合布朗粒子的扩散,表示如下[35]:
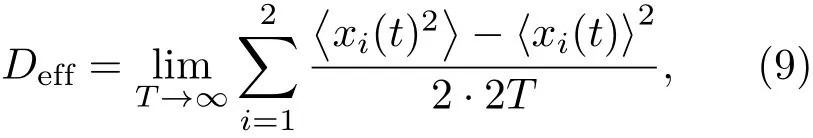
式中T为耦合粒子的演化时间.对于反馈棘轮来说,仅知道⟨Vcm⟩和Dfi还不足以对耦合粒子的输运性能进行全面了解,因此本文进一步对脉冲棘轮的能量转换效率η做了详细讨论,具体表示如下[36]:
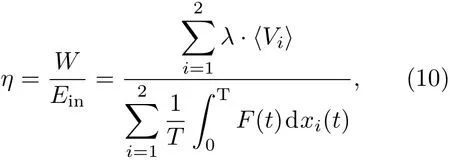
其中⟨Vi⟩为粒子的平均速度.(10)式表明脉冲棘轮的能量转化效率为一段时间内耦合粒子拖动负载所做的有用功W与周期外力输入到反馈棘轮的总能量Ein之比.
本文采用龙格-库塔算法对方程(1)和(2)进行数值计算,主要研究耦合粒子拖动负载时的输运性能随系统各参量的影响.为了得到稳定的系综平均值,本文模拟了5×103条轨道,每个轨道演化了10个周期,且步长取h=1×10−3.文中所有物理量采用无量纲化参量,无特殊说明参数取L0=1.0,γ=1.0,G=0.4,ω =0.8,τ=10.
3 结果与讨论
3.1 反馈脉冲棘轮的定向输运
3.1.1 耦合自由长度b的影响
为了研究脉冲棘轮的定向输运,本文研究了不同耦合强度k下粒子质心的平均速度随耦合长度b的变化关系,如图1(a)所示.研究结果表明,无耦合情况下,即k=0时布朗粒子的质心平均速度随自由长度的变化趋于某一恒定值.说明无耦合情况下自由长度对两个自由粒子的平均速度没有影响.k=0时,随着自由长度b的增加,反馈脉冲棘轮的质心平均速度呈周期性变化.研究发现,在每个演化周期内几率流都会出现极值.当b=1.0时,在一个演化周期内粒子的自由长度最长,此时粒子间的相互作用最弱.因此耦合粒子容易跨越势垒形成定向运动,从而使反馈棘轮的定向输运达到最强.类似的分析可知,在每个演化周期内脉冲棘轮也会存在某一自由长度b使耦合粒子质心的平均速度达到最小.这一现象表明,由于耦合自由长度与棘轮势场空间周期的竞争关系,使粒子处于势阱中不易跨越势垒,因此反馈棘轮很难形成定向输运.更有趣的是,对于一定的自由长度随着耦合强度k的增加,脉冲棘轮的平均速度反而减小.特别是当耦合粒子的相互作用较强时,如k>50后反馈棘轮的输运从正向变为负向,说明强耦合作用下反馈脉冲棘轮能够产生流反转现象.关于耦合强度对粒子定向输运的影响将在下文进行深入讨论.
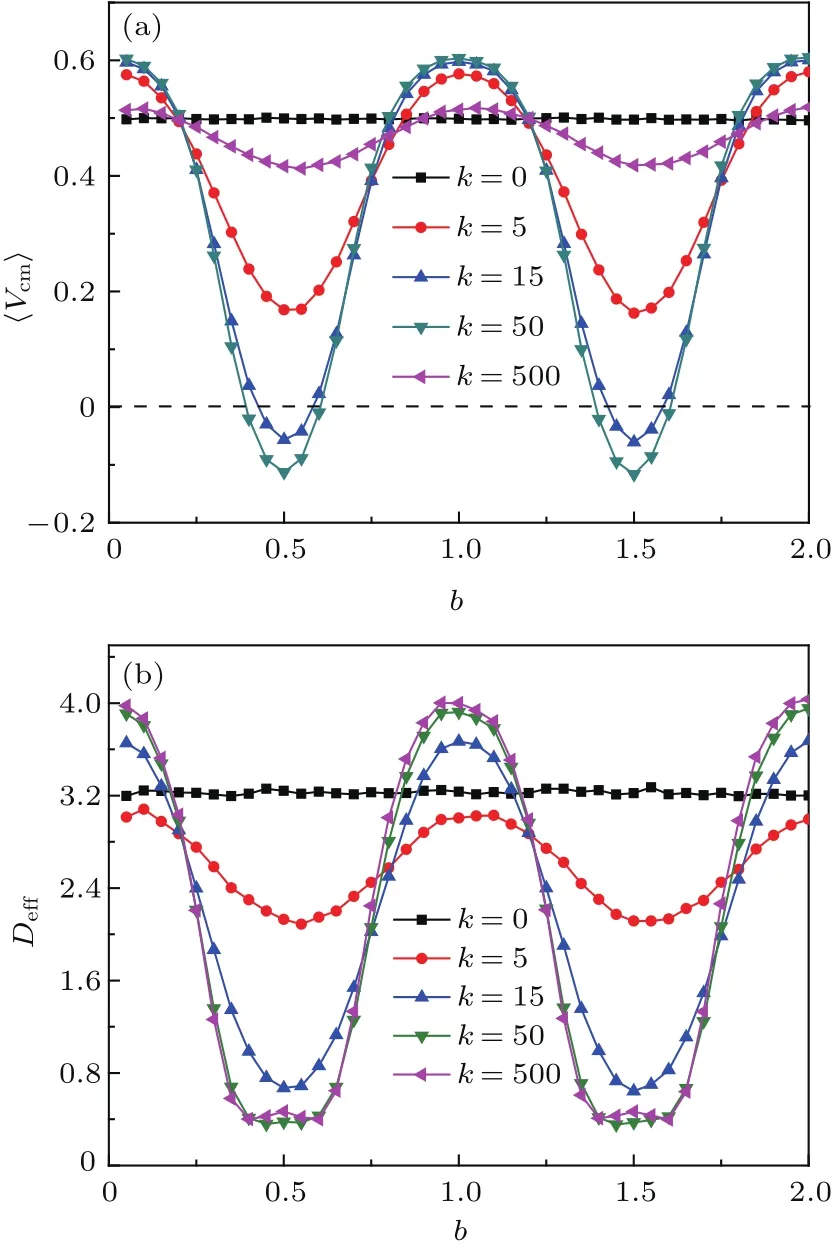
图1 (a)质心平均速度⟨Vcm⟩,(b)平均有效扩散系数Dfi随自由长度b的变化曲线,其中C=3.0,λ=0.12,φ=π/5Fig.1.The curves of(a)the center-of-mass velocity⟨Vcm⟩,(b)the average effective diffusion cofiicient Dfivarying with the free length b,where C=3.0,λ=0.12,φ=π/5.
在噪声背景下,耦合粒子会发生自由扩散运动.本文进一步研究了粒子的平均有效扩散系数Dfi随自由长度的变化关系,如图1(b)所示.研究发现,无耦合情况下,即k=0时,布朗粒子的平均有效扩散系数Dfi随自由长度的变化是在某一恒定值附近变化.即此时两个粒子是在做自由扩散运动.k=0时,耦合布朗粒子平均有效扩散系数的变化同粒子质心平均速度的变化有类似规律,随自由长度b的增加,Dfi也呈现周期性变化.在一个演化周期内,如b=1.0时,粒子间的自由长度最长,此时粒子更容易做自由扩散,所以耦合粒子的扩散系数Dfi也相对较大.也就是说在一定条件下自由长度能使耦合粒子达到较强的扩散.然而,在演化周期内自由长度为某一合适值,如b=0.5时,从图1(a)的分析可得此时脉冲棘轮的平均速度较小,也就是说耦合粒子位置的变化较慢.根据(9)式不难发现,此时耦合粒子位置的涨落也相对较小,所以脉冲棘轮的自由扩散会较弱.说明一定条件下自由长度将会抑制耦合粒子的扩散.研究还发现,一定b的情况下耦合强度k=500比k=15时的扩散系数更小.这是因为k较强,两个粒子的相互作用可看成一个硬杆,从而导致耦合粒子的协调性大大降低,因而耦合粒子更不容易产生自由扩散运动.然而,当k较大时,如k=50和k=500时,粒子的自由扩散系数趋于一致,下文将详细讨论耦合强度对脉冲棘轮自由扩散的影响.
3.1.2 耦合强度k的影响
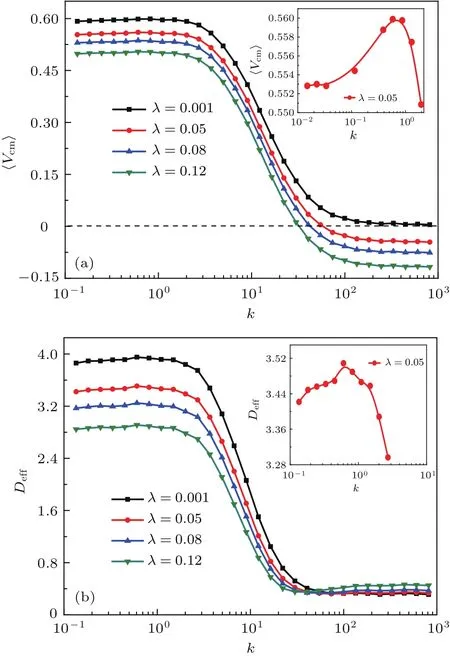
图2 (a)质心平均速度⟨Vcm⟩,(b)平均有效扩散系数Dfi随耦合强度k的变化曲线,其中b=0.5,C=3.0,φ=π/5Fig.2.The curves of(a)the center-of-mass velocity⟨Vcm⟩,(b)the average effective diffusion cofiicient Dfivarying with the strength of coupling k,where b=0.5,C=3.0,φ=π/5.
上述研究表明,耦合强度对脉冲棘轮的输运有一定影响.因此,本文进一步研究了不同负载λ作用下粒子质心的平均速度随耦合强度k的变化关系,如图2(a)所示.研究结果表明,k→ 0时,即弱耦合条件下反馈脉冲棘轮的定向输运相对较弱.以λ=0.05为例,研究发现,随着k的增加且k<10时,如图2(a)插图所示,反馈棘轮的输运会出现极大值.这一现象表明较弱的耦合强度能使脉冲棘轮的定向输运达到最强.这一结论与熵垒中活性布朗粒子的输运行为有类似的结果[37,38],但产生机理并不完全相同.当耦合强度继续增加,发现不同负载λ作用下脉冲棘轮的⟨Vcm⟩都迅速减小,说明强耦合作用将抑制脉冲棘轮的定向输运.然而,当k>100后,研究发现随着负载的增加,耦合粒子的平均速度会减小并趋于稳定,且当λ>0.001后,⟨Vcm⟩<0.说明较大的负载作用将会拖动粒子,从而使反馈脉冲棘轮产生反向运动.
为了进一步研究耦合粒子的扩散运动,进一步讨论了不同负载作用下耦合强度k对反馈脉冲棘轮扩散的影响,如图2(b)所示.研究结果表明,当k<1时,不同负载λ作用下耦合粒子的平均有效扩散系数Dfi均缓慢增加,并会产生极大值,如图2(b)插图所示.说明弱耦合作用会促进耦合粒子的自由扩散运动.然而,当k>1后,不同负载作用下耦合粒子的平均有效扩散系数Dfi均迅速减小,且逐渐趋于稳定值,说明较大的耦合强度将抑制耦合粒子的自由扩散.综上所述,对于反馈脉冲棘轮来说,为了获得较强的定向输运,选取合适的相互作用和负载是十分必要的.
3.2 反馈脉冲棘轮的能量转化效率
3.2.1 自由长度b的影响
图1(a)的研究结果表明,自由长度能够增强棘轮的定向输运,因此,本文进一步研究了反馈脉冲棘轮的能量转化效率随自由长度b的变化关系,如图3所示.研究发现,不同的耦合强度下,脉冲棘轮效率随自由长度b的变化仍呈现周期性.在一个演化周期内,存在合适的b值使耦合粒子的能量转化效率达到最大.根据能量转化效率的定义(10)式可知,在一定条件下η和⟨Vcm⟩的变化呈类似的正比关系.因此当脉冲棘轮的定向输运较强,如b=1.0时,耦合粒子拖动负载做功的能力也相对较大.说明合适的弹簧自由长度能够促进反馈脉冲棘轮的能量转化效率.同理可分析,在一个演化周期内,当0.75<b<1.0时,随耦合强度的增加,脉冲棘轮的能量转化效率也随之增强.说明一定条件下合适的耦合强度也能促进反馈脉冲棘轮的能量转化.此外,图1(a)的研究结果表明,在一个演化周期内,自由长度为某一合适值时,如b=0.5,强耦合作用会使耦合粒子呈反向运动.此时由(10)式计算得到的效率在一定自由长度范围内为负,表明在此区间研究反馈脉冲棘轮的能量转化效率没有实际意义.
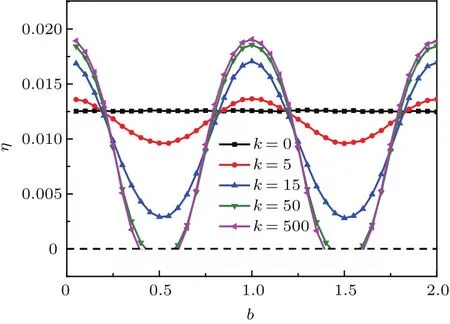
图3 能量转化效率η随自由长度b的变化曲线,其中φ=π/5,C=3.0Fig.3.The energy conversion fiiciency η varying with the free length b,where φ = π/5,C=3.0.
3.2.2 耦合强度k的影响
为了更深入地了解耦合强度对棘轮输运性能的影响,本文进一步研究了粒子能量转化效率随耦合强度k的变化关系.然而图2(a)的研究结果表明,强耦合作用下耦合粒子的⟨Vcm⟩<0,此时研究反馈棘轮的能量转化效率没有意义.因此在不影响分析的前提下都取⟨Vcm⟩>0时的耦合强度范围进行研究,结果如图4(a)所示.研究表明,在一定负载条件下,如λ>0.001时,耦合粒子的能量转化效率都存在极大值;以λ=0.05为例,结果如图4(a)插图所示.说明合适的耦合强度能够促进脉冲棘轮的定向输运效率.此外,研究还发现,在一定耦合强度下,随着负载λ的增加,耦合粒子的能量转化效率也会增强.为了更深入地了解负载对输运效率的影响,研究了有用功W、输入能Ein及能量转化效率η随负载的变化关系,如图4(b)所示.研究发现,在一定条件下,随着负载λ的增加,反馈棘轮的能量转化效率呈单调变化关系.这是由于随着λ的增加,耦合粒子拖动负载所做的有用功W逐渐增加,而此时反馈脉冲棘轮获得的输入能Ein反而减小.因此,由(10)式的定义可得在一定耦合强度下,反馈棘轮的效率随负载是增加的.说明一定条件下负载作用也能增强反馈脉冲棘轮的能量转化效率.此外,当负载较小时,如λ=0.001,不同耦合强度下粒子的能量转化效率为一个非零有限值,说明较小的负载作用很难促进反馈脉冲棘轮的定向输运效率.因此,为了促进脉冲棘轮的能量转化,实验上可以选择合适的耦合作用及负载能够使脉冲棘轮的能量转化效率达到最大.
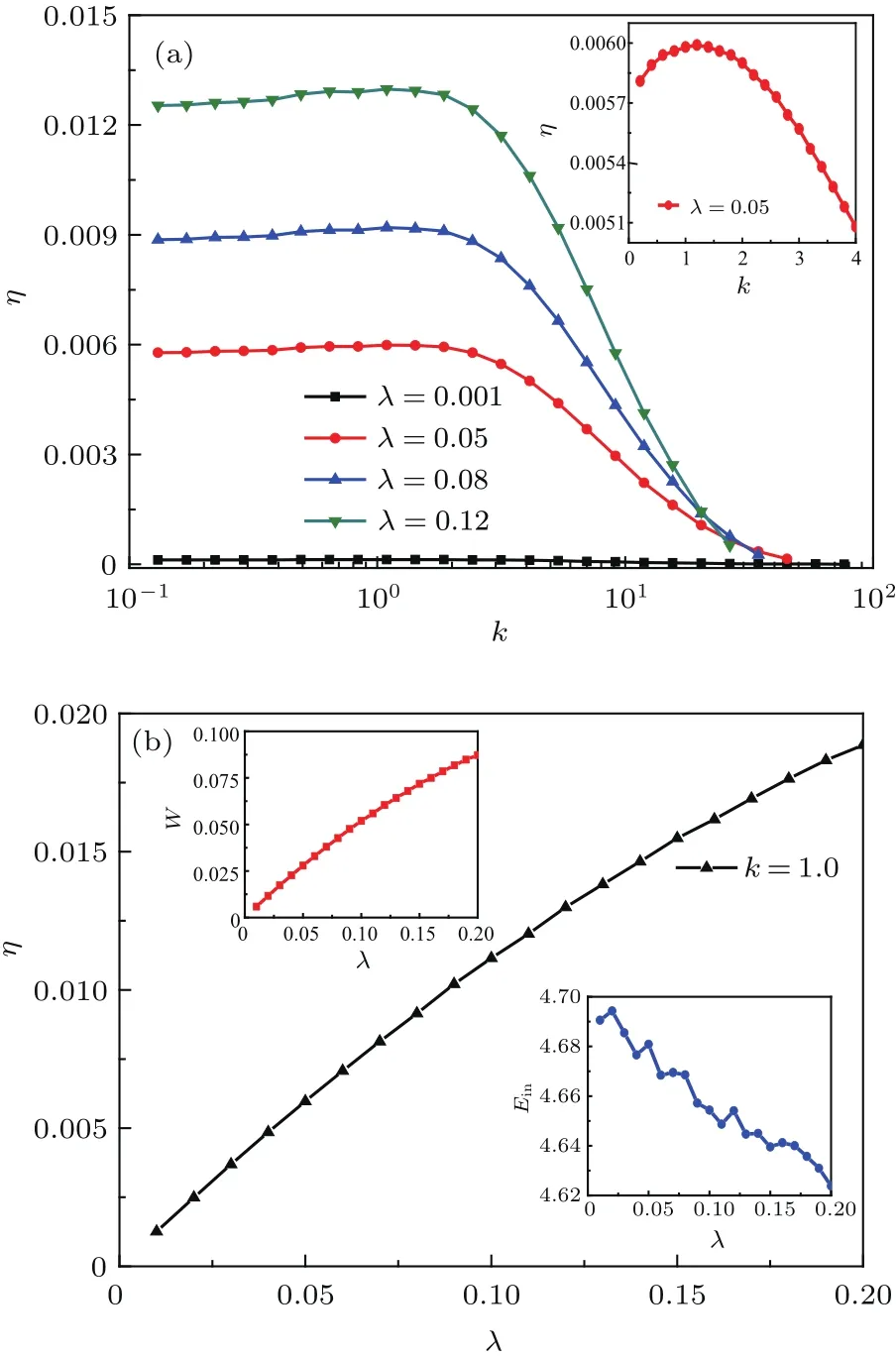
图4 (a)能量转化效率η随耦合强度k的变化曲线,其中φ=π/5,C=3.0,b=0.5;(b)有用功W、输入能Ein、能量转化效率η随负载λ的变化曲线,其中k=1.0,φ=π/5,C=3.0,b=0.5Fig.4.The curves of(a)the energy conversion fiiciency η varying with the strength of coupling k,where φ = π/5,C=3.0,b=0.5;the curves of(b)the useful work W,the input energy Einand the energy conversion fiiciency η varying with the load λ,where k=1.0,φ=π/5,C=3.0,b=0.5.
3.3 反馈脉冲棘轮的流反转
3.3.1 脉冲相位θ的影响
上述研究表明,自由长度及耦合强度都能增强反馈脉冲棘轮的定向输运.为了更深入地理解脉冲棘轮的输运行为,本文研究了不同自由长度下耦合粒子质心的平均速度随脉冲相位的变化关系,如图5(a)所示.由于棘轮受到的反馈脉冲作用g1(t)具有周期性,因此耦合粒子的定向输运行为随脉冲相位φ的变化仍将呈现周期性.此外,在一个脉冲周期作用下,如b=1.5时,当φa<φ<φm时,随着相位φ的增加,耦合粒子质心的平均速度会逐渐减小,且在φ=φm时达到负向最大.当φm<φ<φn时,随着相位φ的继续增加,反馈棘轮的输运速度会反向减小,且在φ=φn时达到了正向最大.为了分析脉冲棘轮的流反转现象,本文详细研究了不同相位下耦合粒子质心位移随时间t的演化行为,如图5(b)所示.以b=1.5为例,当脉冲相位φ=π时,耦合粒子质心位移⟨xcm⟩的总体演化趋势是减小的,平均而言耦合粒子的输运速度为负.因此随着脉冲相位的增加,反馈棘轮的定向输运会呈反向运动.同时,图5(a)所示的概率流在φ=φm处出现极小值,说明合适的脉冲相位能够使反馈棘轮的反向输运达到最强.然而,当φ>φm时,发现耦合粒子的运动会从负向变为正向,说明在脉冲作用的一个周期内反馈棘轮产生了第二次的流反转现象.对于此时的流反转仍可用图5(b)进行类似的讨论.例如当φ=2π时,图5(b)中耦合粒子质心位移的总体演化趋势随时间变化是上升的,所以随着脉冲相位的增加,如φ>φm后脉冲棘轮的输运会呈现第二次的流反转.随着脉冲相位的继续增加,耦合粒子的速度将达到正向最大,如φ=φn.此时说明合适的脉冲相位也能使反馈棘轮的正向输运达到最强.此外,研究还发现对于一定的脉冲相位反馈棘轮的输运不是自由长度b的单调函数,这一结果与图1(a)的研究结论一致.因此通过选择合适的脉冲相位能够对生物医学上粒子分离、药物投放等相关输运过程提供一定的理论指导.
为了更深入地理解反转输运时耦合粒子的扩散行为,图5(c)进一步研究了不同自由长度下耦合粒子的平均有效扩散系数随脉冲相位φ的变化关系.研究发现:粒子的平均有效扩散系数随脉冲相位φ的变化也呈周期性;在一个脉冲周期内,存在合适的相位φ使耦合粒子的Dfi获得两个极小值.说明合适的脉冲相位能够有效抑制耦合粒子的自由扩散,并在一定程度上促进了脉冲棘轮的输运.此外,对于一定的脉冲相位,随着b的增加,脉冲棘轮的平均有效扩散系数不是单调的.说明一定条件下,选择合适的自由长度也能够抑制脉冲棘轮的扩散,所得结论与图1(b)的研究结果一致.

图5 (a)质心平均速度⟨Vcm⟩随脉冲相位φ的变化曲线,其中k=10.0,C=2.0,λ=0.12;(b)质心平均位移⟨Xcm⟩随时间t的变化曲线,其中k=10.0,C=2.0,λ=0.12;(c)平均有效扩散系数Dfi随脉冲相位φ的变化曲线,其中k=10.0,C=2.0,λ=0.12Fig.5.The curves of(a)the center-of-mass velocity varying with the phase difference between pulsations of two particles,where k=10.0,C=2.0,λ=0.12;the curves of(b)of center-of-mass displacement varying with the time t,where k=10.0,C=2.0,λ=0.12;the curves of(c)the average effective diffusion cofiicient Dfivarying with the phase difference between pulsations of two particles,where k=10.0,C=2.0,λ=0.12.
4 结 论
本文研究了负载拖动下相互作用布朗粒子的定向输运行为.同时,耦合棘轮还将受到时变的反馈脉冲作用.本文详细讨论了弹簧自由长度、耦合强度及脉冲相位对耦合粒子质心的平均速度、平均有效扩散系数Dfi以及粒子能量转化效率的影响.研究发现,一定自由长度及耦合强度能够促进反馈脉冲棘轮的定向输运,并能提高耦合粒子拖动负载时的能量转化效率.发现一定的脉冲作用能够诱导反馈棘轮在一个演化周期内产生两次流反转.此外,通过选择合适的脉冲相位能够有效抑制耦合粒子的自由扩散,从而一定程度上促进了脉冲棘轮的输运.研究还发现,合适的负载作用也能提高反馈脉冲棘轮的能量转化效率.本文所得结论不仅能够应用于粒子的筛选、分离及提高粒子输运效率等方面,也对生物医学上药物投放等相关纳米量级输运过程有一定的启发.

