声学超材料与超表面研究进展∗

丁昌林 董仪宝 赵晓鹏

(西北工业大学理学院智能材料实验室,西安 710129)

(2018年5月15日收到；2018年7月10日收到修改稿)

1 引 言

波是自然界普遍存在的运动形式,而对波的调控研究(包括波的传播方向和物理性质等)既具有广泛的应用价值,又极大地推动了科技的发展.自然界中存在很多材料可以对波(声波、电磁波等)进行调控,材料的响应参数均为正值.而要突破自然界常规材料对波的调控,需要引入新的理念和方法实现波的负参数响应.1968年,苏联物理学家Veselago[1]提出左手材料的概念,并经由Pendry等[2,3]和Smith等[4]分别从理论和实验上加以验证,实现了响应参数介电常数和磁导率同时为负的左手材料,开辟了对电磁波和其他形式波反常调控的新途径.由左手材料发展而来的电磁超材料是一种人工设计的材料,对电磁波具有负折射、反常多普勒、反常切仑科夫辐射、完美透镜、隐身等反常调控效应[5−9].由于电磁波和声波均满足波动的相关性质,有共同的波参数,如波矢、波阻抗和能流等,且均满足波动方程,研究者们将电磁超材料的设计思想延伸到声学领域,设计出对声波产生各种奇异性质的声学超材料.

2 声学超材料研究进展

2.1 声学超材料发展概况

2000年,Liu等[10]首次提出利用局域共振型的结构单元构建声学超材料,这一思想为声学超材料的研究开辟了一个全新的途径,这种基于硅胶-铅球核壳结构的声学材料具有低频带隙,且在低频带隙附近其有效质量密度为负值.与电磁超材料研究方法类似[2−4,11,12],在声学领域人们关注的重点是如何实现负质量密度、负弹性模量以及双负声学超材料.研究者们首先从理论上提出相关模型实现负质量密度[13−15].2008年,Yang等[16]从实验上提出并制备了一种二维薄膜-质量块结构的负质量密度声学超材料,并系统研究了以这种结构为基础的声学超材料的奇异性质[17,18].与此同时,研究者通过很多方法实现了负质量密度声学超材料[18−27],并通过研究各向异性的质量密度材料[28−32]拓宽了声学材料的属性范围.2006年,Fang等[33]提出了一种由亚波长尺度的一维亥姆霍兹共振腔阵列和传播通道组成的超声超材料,这种材料在共振频率附近的弹性模量为负值.受Fang等的启发,研究者们提出了多种负等效弹性模量模型.将亥姆霍兹共振器模型推广至二维和三维情况,也可以得到负弹性模量声学超材料[34−37]；通过在空心管侧壁开孔的方式[38],可以实现一种具有传播截止频率的负等效弹性模量声学超材料；Ding等[39−44]提出了一种开口空心球结构,实现了空气介质中的负等效弹性模量；Leroy等[45]通过气泡阵列实现了负弹性模量.相较于单负声学超材料,弹性模量和质量密度同时为负的双负声学超材料具有更多的奇异性质[46].双负超材料主要是将两种单负超原子结构组合在一起实现的.Ding等[47]提出了一种闪锌矿结构,由水球包覆气泡的结构和环氧树脂中橡胶包覆金球的结构组成,理论上能同时实现负等效质量密度和负等效弹性模量.Lee等[48]将周期性排列薄膜的空心管结构和侧壁打有周期性孔洞的管状亥姆霍兹共振器结构组合在一起实现了双负声学超材料,且测试了其反常多普勒效应[49].Chen等[50−53]将负质量密度的空心管结构和负弹性模量的开口空心球结构组合在一起可以实现双负声学超材料,同时将两种结构耦合成一个超分子也可以实现双负声学超材料.Fok和Zhang[54]提出将亥姆霍兹共振器和有机玻璃包覆的铝柱在同一个铝制体腔中耦合,制备出了双负和负折射率声学超材料.而单一的结构单元如果存在两种共振模式,也可以实现双负超材料.Yang等[55]设计了一种双薄膜系统,通过调整单极共振和偶极共振的共振频率,实现了520—830 Hz范围内的双负声学参数.Lai等[56]设计了一种基于固体基底的弹性声学超材料,可以实现两个双负色散带.Pope和Daley[57]提出一种黏弹性双负声学超材料理论模型,其负动态质量密度和弹性模量均可调谐.

通过超原子和超分子设计的声学超材料具有很多奇异性质[58−60],包括平板聚焦、负折射、亚波长成像、隐身、反常多普勒效应、异常声透射等.不同于声子晶体[61,62],声学超材料是基于具有共振原理实现负折射聚焦的.基于声学传输线模型[63,64],利用两种亥姆霍兹共振器的组合可以实现水介质中的超声聚焦.将亥姆霍兹共振器或迷宫状结构设计成二维声学超材料[65,66],在实验上可以实现负折射效应.García-Chocano等[67]利用一种双曲超材料同样实现了负折射效应.Xia和Sun[68]设计了一种非共振的环状结构,通过其在特定本征频率下的固有模式,实现了声波在环结构中心的聚焦.Zhai等[52]通过一个钻孔空心管构成的楔形样品,实现了空气介质中可听声频段的负折射现象.

类比于电磁领域的表面等离激元放大倏逝波原理[69−71],在声学领域利用负等效质量密度声学超材料可以放大倏逝波[72],实现超分辨成像的声学近场超棱镜(superlens)[73].实现声学superlens还有其他方法.Zhu等[74]利用周期性排列的孔洞结构产生的法布里-珀罗共振耦合可以将声倏逝波放大,实现近场超分辨成像(λ/50)；Kaina等[75]利用单一共振器制备的单负超材料可以实现负折射率声学superlens.与电磁远场透镜(hyperlens)[76−78]设计方法类似,利用声学超材料也可以实现倏逝波的远场放大[79−82],实现声学远场超分辨透镜.Li等[83]提出了一种基于扇形结构的二维声学远场超透镜,可以对宽频声波实现亚波长远场超分辨成像,分辨率达到λ/6.8—λ/4.1.

利用声学超材料还可以设计声学完美吸收器[84]. 2010年,Pai[85]从理论上提出了宽频带弹性波吸收器,使声波完全吸收成为可能.Mei等[86]利用基于附加金属片的薄膜的共振实现了100—1000 Hz低频域的宽频吸声,并且在172 Hz时吸声效率达到86%.将薄膜做成双层以后,在某些频率吸声率达到99%.Ma等[87]设计了一种薄膜结构和空气通道相组合的窄频选择性滤波器.近几年来,研究者们通过很多种方法来设计声学超材料实现声波的高效率吸收[88−91].

声学超材料可以实现对声波的隐身效应.以Pendry等[92,93]提出的电磁隐身斗篷设计方法为基础,Chen和Chan[94]提出用球形Bessel函数系展开的方法解决声散射问题,设计出一种三维声学隐身斗篷[95,96].将变换声学公式改进,理论上可以利用多层同心柱结构实现声隐身[97−99].由于隐身材料对材料参数要求非常高,实验制备比较困难,Zhang等[100]通过引入声学传输线理论克服了上述难题,设计了一种二维的圆柱形斗篷,实现52—64 kHz宽频段的超声隐身.Zhu等提出通过单负超材料也可以实现声隐身[101].为了避免复杂的参数设计,将斗篷设计成菱形结构,仅利用均匀介质可以实现声隐身[102,103]；在此基础上,Zigoneanu等[104]通过理论设计并实验实现了一种近乎完美的三维、宽频带、全方位三维地毯式隐身斗篷.

2006年,Hu等[105]在一种声子晶体的带隙中实验实现了反常多普勒效应.Lee等[49]利用所设计的双负声学超材料同样实验实现了这种反常多普勒效应.Zhai等[106]利用超分子簇制备的声学超材料实现了宽频带反常多普勒效应.

声学超材料还可以用于实现声学异常透射效应[107−109],对波长较长的声波的远距离声学准直[110],设计声学二极管,实现声波能量非导易传播[111−116].在短短的十几年间,声学超材料已经得到了飞速的发展,产生了许多新的奇异性质,并且被应用到了许多领域,如超声成像、水下声学和声呐、建筑声学和吸声材料等.

2.2 超原子声学超材料

2.2.1 负弹性模量超原子

声学超材料的奇异特性主要通过设计合适的人工声学超原子来实现.在电磁学领域,作为一种人工超原子,开口的金属环(SRRs)具有局域共振性质,并可以用于制备负磁导率材料[3].利用类比的思想,在声学领域也能找到一种局域共振的超原子——开口空心球(SHS)结构单元[39−44].图1(a)所示的SHS为带有一定直径孔洞的空心球,SHS的体腔具有储存声能的功能,开口处会引起声媒质进出振动,当达到谐振频率时,体腔中积累的能量使得声媒质在开口处发生强烈的振动而实现共振,且共振单元是制备声学超材料的基本超原子,其谐振频段为

图1 负弹性模量声学超材料 (a)结构示意图；(b)透射率曲线；(c)透射相位曲线；(d)等效弹性模量Fig.1.The acoustic metamaterial with negative modulus:(a)the schematic diagram of SHS unit cell and sample；(b)the curve of transmission；(c)the curve of transmission phase；(d)the effective modulus.

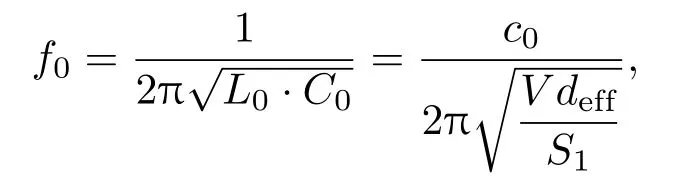
其中S1=π(d/2)2为开孔的横截面积；V为SHS的空心球体积；ρ0,c0为空气的密度和声速.在共振时,开口处的声辐射会产生辐射阻抗,增加√了开口管的等效长度,经过修正得到dfi=t+1.8d.

实验中制备合适尺寸的SHS单元,将结构单元周期性排列在海绵基底上可以制备出声学超材料样品.实验测试得到SHS样品的透射曲线(黑线所示)在f=5 kHz附近出现强烈的吸收峰.究其原因,由于超原子SHS体腔对外开放,入射声波的能量大量存储在空心体腔中,体腔中积累的能量也可以从开口处释放出来.根据SHS的几何设计与共振模型可知,吸收峰的位置刚好和SHS的共振频率一致,说明吸收峰是由SHS的局域共振引起的,而排有SHS结构的材料在5 kHz附近出现相位波动,产生反相的变化规律,其他地方相位变化均匀.此时可以看出,在5 kHz附近SHS样品同时出现吸收峰和相位突变,与电磁领域中的SRRs负磁材料的性质相似.

通过测算，可以综合判断不同产品的盈利能力水平，并作为业务审批的必要判断依据，低于目标值的业务及客户，可以与客户进行谈判，通过改善定价、增加派生业务收益等来提升综合收益贡献，或者通过增加缓释等方式降低风险及资本成本。

SHS样品由于微结构单元的谐振,在谐振频段出现负的动态响应,且基本单元的尺寸远小于波长,可以看成均匀介质.根据均匀介质理论[117],利用实验测试的透射系数和反射系数可以得到该声学超材料折射率和等效阻抗,通过等效阻抗和折射率可以计算出声学超材料的等效弹性模量.实验数据计算表明,SHS声学超材料在谐振频率5 kHz附近的弹性模量为负值,且弹性模量的虚部在谐振频率附近也有强烈的衰减,如图1(d)所示.

2.2.2 负质量密度超原子

类比电磁学中金属杆阵列[2]实现等效介电常数ε＜0,在声学领域提出了可实现负质量密度的空心管(HT)人工超原子共振模型[26,50],如图2(a)所示.HT是两端开口的空心钢管结构.两端开口的圆柱形空心管对声波具有引导作用,可以将这种结构等效看成声学电路的电感L=ρ0l/S,S是端口截面积,l是孔径长度.空心管内部可以看成一种体腔,具有存储声波能量的功能,相当于声容的作用,因此等效声容C=V/(ρ0c20),其中V是空腔的体积,c0是流体中的声速,ρ0是背景流体的密度.基于L-C共振模型计算的谐振频率为

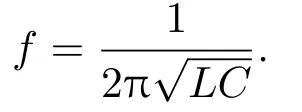
利用声学阻抗管,当声波传播到超材料表面时,可以测试出其透射率和透射相位曲线,经过测试在频率大于1540 Hz时出现透射禁带,同时伴随出现相位突变.说明空心管样品在此频率范围内发生了谐振,这是由于排列在海绵基底上的空心钢管长度不同产生的声学效应所致.究其原因,声波是一种纵波,入射声波能量大量储存在空心钢管中,因此空心钢管可以看成谐振单元,在共振频段具有谐振性质,与电磁学中的金属杆等离子体谐振产生负介电常数的性质类似.空心钢管样品由于微结构单元的谐振,在禁带范围内出现负的动态响应.

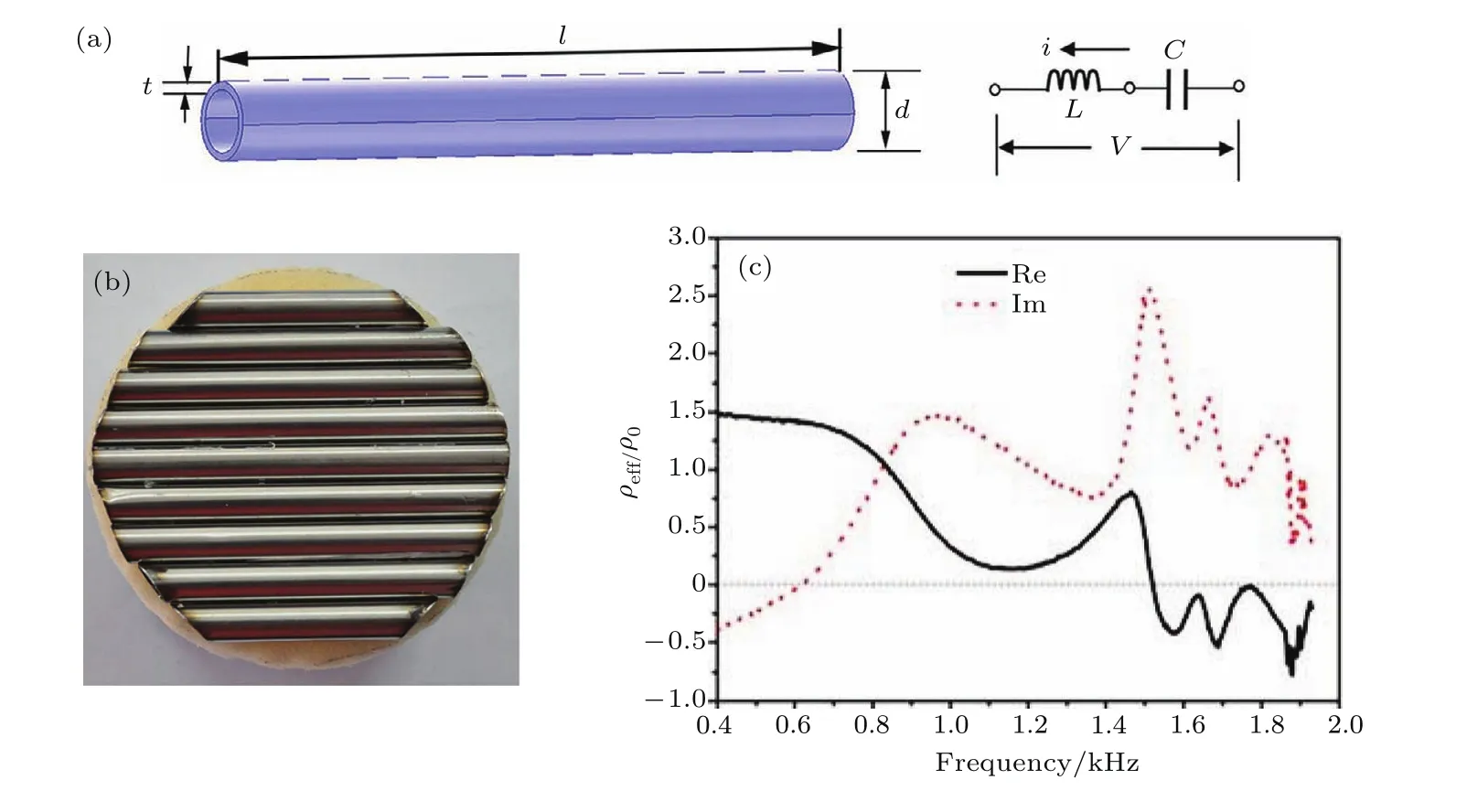
图2 负质量密度声学超材料 (a)空心管结构单元；(b)空心管声学超材料；(c)等效质量密度曲线Fig.2.The acoustic metamaterial with negative density:(a)The unit cell of hollow steel tube(HT)structure；(b)HT acoustic metamaterial；(c)the curves of effective mass density.

通过实验数据计算可以得到声学超材料的等效质量密度,如图2(c)所示.从图中可以看出等效质量密度的实部从1548 Hz以后为负,在1584 Hz达到负的最大值,说明空心管结构可以实现负质量密度声学超材料.

2.2.3 双负超原子

从前面的讨论可知,SHS能实现负的弹性模量,空心管结构能实现负的质量密度.类似于开口金属环和金属杆结构组合制备出电磁左手材料,将空心管结构和SHS结构叠加起来,组成双层SHS和双层空心管模型用以制作双负的声学超材料[50],如图3(a)所示.在阻抗管中测试了其声学透射、反射性质.实验结果表明该声学超材料在1540 Hz左右有一个吸收峰,随后透射增强,透射增强的频带对应着相位突变.吸收峰对应的透射率比只有双层SHS和只有双层HT时的透射率都低,原因是此时的SHS的谐振频率和HT的谐振频率没有匹配造成的；而透射峰对应的透射率比单纯SHS和单纯HT的最高透射率都高,再考虑到双层SHS和双层HT多了两层海绵的吸声作用,透射峰的形成应该是SHS和HT的共同谐振造成了一个声波通带.

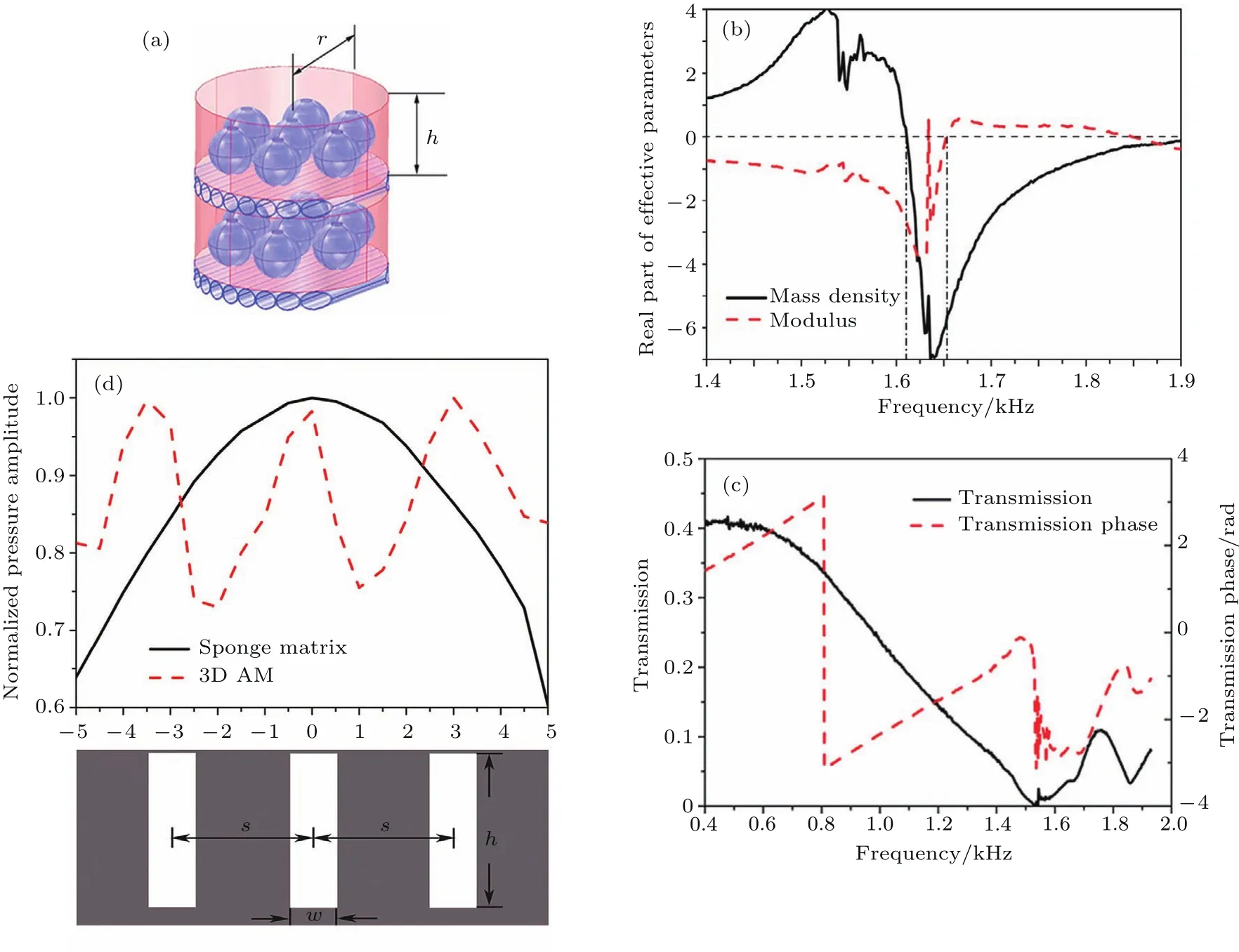
图3 双负声学超材料 (a)结构示意图；(b)透射率和相位曲线；(c)等效参数曲线；(d)亚波长成像图Fig.3.The double-negative acoustic metamaterial:(a)The schematic diagram of the sample；(b)the curve of transmission amplitude and phase；(c)the effective parameters；(d)the results of sub-wavelength imaging.

为了说明声波通带产生的原因,实验同时测试了声学超材料的反射系数,利用等效参数提取法得到这种材料的质量密度、弹性模量.图3(b)表明该声学超材料的质量密度和弹性模量在1612—1654 Hz范围内都为负值.双负声学超材料具有很多奇异性质,我们实验测试了这种超材料的亚波长成像效应.将声喇叭放置于双负超材料前面80 mm,利用一个带间距为30 mm的三个方形孔洞的金属挡板产生三个子波源.这三个方形子波源距离双负超材料5 mm.选择喇叭产生的声波频率刚好在双负频段的1630 Hz(λ=200 mm).当三个子波源的声波入射到双负超材料后,会在后面形成声场分布,对于正常材料,这三个子波源是无法分辨开的,因为根据衍射极限,波的分辨率最大为半波长,即100 mm.若选用海绵测试,三个声源无法分开,而利用双负超材料实验,可以将三个声源分辨开,可以测试出超材料后面具有三个透射峰,刚好代表三个子声源,如图3(d)所示.说明这种双负超材料的分辨率已经突破了衍射极限,根据分辨的距离可知,这种超材料的分辨率能达到λ/7.

2.3 超分子声学超材料

一个超分子可以由两个超原子整合形成,通过一种超分子结构也可以实现双负声学超材料[118,119].将具有负质量密度的空心管超原子和具有负弹性模量的开口空心球超原子融合到一起,可以设计出一种开有侧孔的空心管结构单元,也称为“类笛子”声学超分子结构.利用该超分子结构单元,分别在低频和高频实现了双负声学超材料[51,52],并研究了其声学奇异性质.

图4 “类笛子”超分子声学超材料 (a)结构单元；(b)样品示意图；(c)透射系数曲线；(d)声学等效参数曲线；(e)平板聚焦声场分布；(f)负折射效应声场分布Fig.4.Flute-like meta-molecule acoustic metamaterial:(a)The structure of meta-molecule；(b)the schematic diagram of the sample；(c)the curves of transmission cofiicient；(d)the curves of acoustic effective parameters；(e)the acoustic field distribution offlat focusing；(f)the acoustic field distribution of negative refraction.

如图4(a)所示,开口空心球和空心管两种超原子都是亚波长的局域共振结构单元,可以等效成L-C振荡电路.结构单元内部的空气流动可以看作是振荡电路中的电荷流动.对于空心管,空气在空心管的两个端口进出,使封闭在空腔中的流体产生压缩和扩张.因此,管的端口可以看成是声学电路中的声感Lt,而管的空腔可以看成声容Ct,Lt1= ρ0Lt1/St1,Lt2= ρ0Lt2/St2,Ct=Vt/(ρ0c20),这里的St1=St2分别为塑料管端部空腔的横截面积；Lt1,Lt2分别是两个端部的等效长度；Vt是管空腔的体积；ρ0是流体的密度；c0是流体中的声速.SHS相当于一个亥姆霍兹共振器,SHS的开孔和内部空腔分别相当于电感Lp和电容Cp,“超分子”模型可以看成是在一个空心管内嵌入了一个SHS.根据图中所描述的L-C振荡电路,将L和C分别整合在一起,共振的频率可以写成

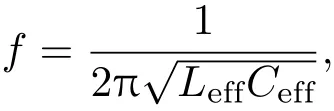
实验制备的超分子单元是一个开有侧孔的中空塑料管,将这种结构单元按照开孔位置“Z”字形周期性间隔排列,并且用黏合剂固定在海绵基底的正反两面,制备成双层超材料样品,如图4(b)所示.其中,海绵是一种非散射性的声学介质,可以用来作为声学基底.在自由空间测试其在3—6 kHz的透射和反射性质.图4(c)透射实验表明,这种超材料在5.5—5.9 kHz范围内具有透射峰,类似左手材料透射通带.由于这种材料的厚度小于λ/7,结合测量的反射数据,利用基于均匀介质的等效参数提取法计算出这种超分子超材料的有效质量密度和有效弹性模量的实部在5.65—5.85 kHz区间内同时为负值,并且在这个区域内,计算得到的折射率接近−1,如图4(d)所示.

为了更好地理解双层“类笛子”超分子超材料的奇异特性,制备的样品被用来研究超材料在双负频率5.7 kHz处的平板聚焦现象.将直径为70 mm的扬声器放置在距离样品入射面中心外10 mm处,垂直入射正弦声波.声波透过样品后由麦克风进行探测.为了得到声场分布,麦克风被安置在一个3D位移台上,在水平方向上步进麦克风,并且记录每一步的声场强度.作为对照,我们首先测试了声波穿过海绵基底时的参考声场分布.透过超材料样品的声场分布如图4(e)所示,图中的声压强度都是归一化的.由图可知,透过超材料样品的声波被聚成了一个明亮的点,焦点的半峰宽度(FWHM)大约为50 mm(5λ/6),接近衍射极限,焦点的中心距离样品10 mm.

利用楔形样品测试出基于超分子超材料具有负折射性质,如图4(f)所示.实验测试表明折射波和入射波位于法线同侧,说明超材料实现了负折射效应.

2.4 超原子簇和超分子簇声学超材料

实验研究表明,周期性排列的单个空心管“超原子”的声学行为基本不受周围“超原子”的影响,它们之间也存在弱相互作用.利用空心管“超原子”的这种行为,制备了长短不同的空心管超分子团簇单元.将超分子团簇周期性排列在海绵基底中制备出声学超材料[26],如图5(a)所示,实验测试表明这种超材料具有宽频带的吸收峰,且在宽频范围内实现了负有效质量密度,如图5(b)所示.

开口空心球超原子具有局域共振的性质,将3种不同开口孔径SHS超原子排列在海绵基底上,可以制备出多频带的负弹性模量声学超材料.这三种SHS超原子的球直径为25 mm,球壁厚0.7 mm,开口孔径分别为3,5,6 mm.图5(c)的透射实验表明制备这种超材料分别在914,1298,1514 Hz出现透射吸收峰,这三个吸收峰频段刚好对应三种SHS超原子的共振频率,且通过基于均匀介质的等效参数法,在三个吸收峰频段,超材料的弹性模量同时为负值,如图5(d)所示,说明实现了多频带的负弹性模量声学超材料.结果表明周期性排列的SHS超原子的声学行为不会受到周围其他超原子的影响,SHS超原子之间存在弱相互作用.基于弱相互作用性质,将开口孔径接近的SHS结构组合成超原子簇,可以设计一种宽频带900—1500 Hz的负弹性模量声学超材料[40].

“类笛子”声学超分子也具有弱相互作用,将七种超分子团簇组合成声学超材料[105],仿真计算和实验证实这种局域共振弹性模量和质量密度双负声学超材料可以在宽频实现材料的折射率为负值.实验测试还表明这种超材料表现出宽频反常多普勒效应,并且随频率增加,频移值连续加大,如图6(c)所示.理论上利用超分子团簇可以组装任意宽频双负声学超材料,这也为声学超材料的设计和各种应用开辟了新的途径.

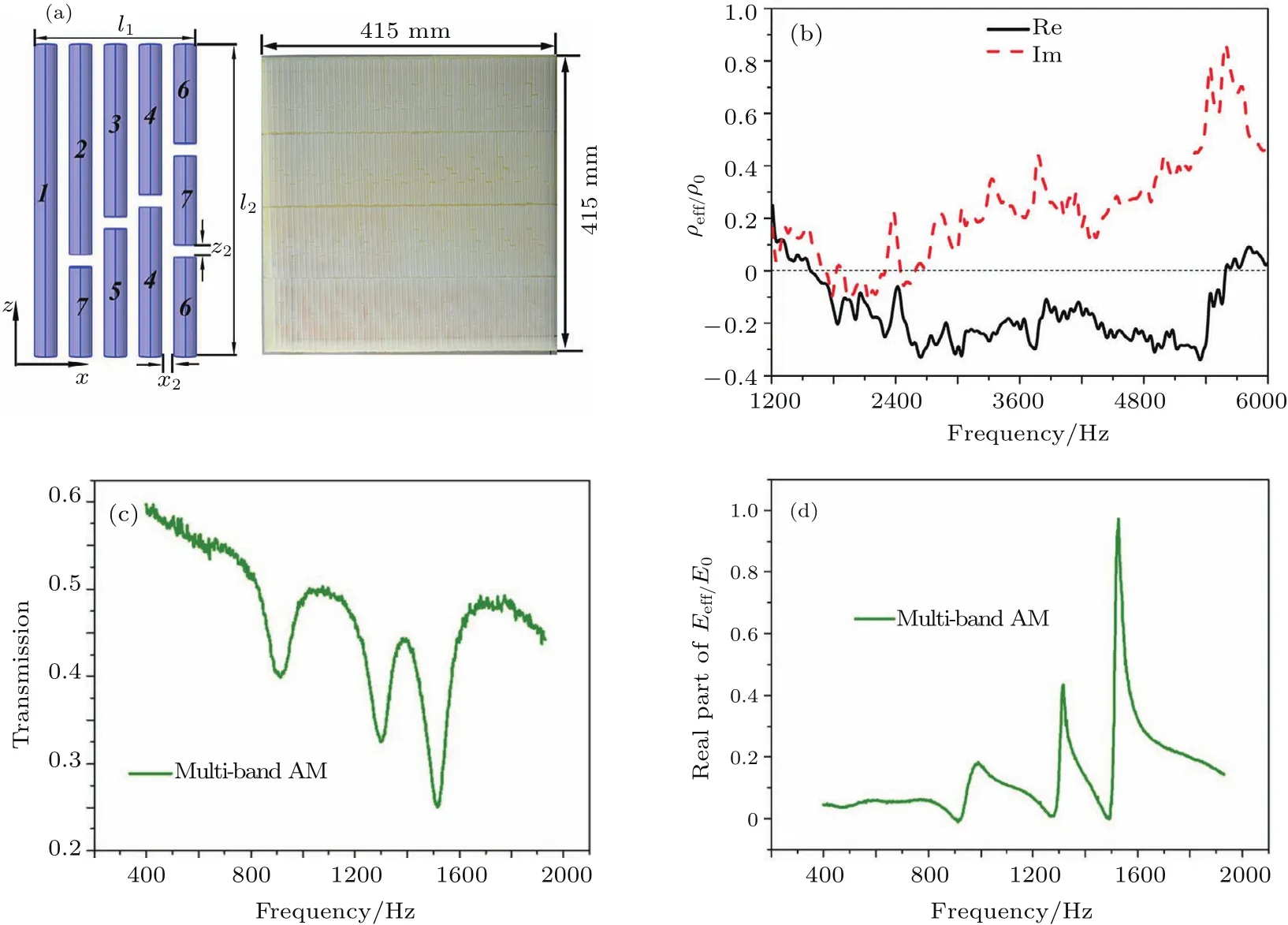
图5 超原子簇声学超材料 (a)宽频带负质量密度声学超材料结构示意图；(b)等效质量密度曲线；(c)多频带负弹性模量声学超材料透射曲线图；(d)等效弹性模量曲线Fig.5.The meta-atom cluster acoustic metamaterial:(a)The scheme of the cluster structure；(b)the curve of effective mass density of broadband acoustic metamaterial with negative mass density；(c)the curve of transmission；(d)the curve of effective modulus of multiband acoustic metamaterial with negative modulus.

图6 超分子簇声学超材料 (a)结构示意图；(b)反常多普勒实验装置示意图；(c)反常多普勒实验结果图Fig.6.The meta-molecule cluster metamaterials:(a)The structure scheme of unit cell；(b)the schematic diagraph of inverse Doppler experiment setup；(c)the experimental results of inverse Doppler experiment.

3 声学超表面研究进展

2011年底提出了一种界面相位不连续的理论[120],通过一种“V”型人工微结构可以设计并制备出厚度远小于波长的材料[121],这种材料被称为超表面材料,它的界面相位不连续,可以根据结构的几何尺寸任意调控0—2π的相位分布,从而任意调控电磁波传播[122−127].由于电磁波和声波的可类比性,电磁超表面的设计思想很快引入到声学领域,利用声学超表面实现对声波传播路径的任意调控[58].首先就是对反射声波传播方向的任意调控.2013年,Li等[128,129]利用卷曲空间结构设计了一种二维的超薄声学超表面,在理论和实验上实现了对反射声波的任意调控.该结构单元沿着声波传播方向上的整体厚度只有1 cm,远小于其工作波长(19.0 cm).Zhu等[130]提出了一种无色散的波前调制方法,设计了一种亚波长由18个具有不同深度凹槽组成的褶皱形表面,可以在宽频范围内实现对反射声波的任意调控.Ding等[131−133]利用具有负等效弹性模量的开口空心球结构设计了一种声学超表面,这种基本结构单元具有很好的耦合性和调谐性,仅通过调节开口空心球的开孔直径调节单元结构在谐振频段0—2π的相位分布,通过仿真和实验证实这种结构可以用来调控声波的传播相位,并且可以实现声波的反常反射现象.Zhao等[134,135]通过改变界面处的阻抗也可以调控声波的传播相位,从而实现声波的反常反射.

除了反常反射以外,声学超表面还可以对透射波实现反常折射.利用超表面调控透射波的方法与反射波类似,通过调节透射波的传播相位,实现透射波传播方向的任意控制,同时要求基本单元的透射效率要尽可能的大,这样利用基本单元设计的声学超表面才能保证对透射波高效率的反常调控；最近几年,已经有不少研究者开始尝试利用声学超表面来实现反常透射现象.Xie等[136]通过螺旋形的迷宫状结构设计了一种声学超表面,其整体厚度约为工作波长的1/2,可以实现明显的反常折射现象.Tang等[137]利用优化过的迷宫结构设计并制备厚度仅为工作波长的1/6.67的声学超表面,实现了对2.25 kHz透射声波的高效率的反常调控.Mei和Wu[138]通过改变结构单元的折射率来调节其相位,同样实现了对透射声波的任意调控.Zhu和Semperlotti[139]利用局域共振环形锥体设计了一种能对入射声波相位进行精确控制的基本单元,利用基本单元构建相位不连续的声学超表面,可以控制薄壁结构件中的弹性导波模式反常折射.Zhai等[140,141]设计的类鼓状结构可以调控透射声波的相位按梯度变化,从而实现对透射声波的反常调控.

声学超表面理论上可以对声波任意调控,近五年来基于超表面的思想实现了很多对声波奇异调控的性质.由亚波长亥姆霍兹共振器阵列组成的声学超表面可以对反射声波定向控制[142].利用超表面可以使得声波非对称传播[143−145]；结合超晶胞周期性和广义反射定律,当入射角超过临界角时,用一种梯度声学超表面能够实现明显的负反射[146].基于声学超表面概念提出的新型超薄平面的施罗德扩散器[147]可以实现令人满意的声漫反射,在建筑声学及其相关领域具有巨大的应用潜力.利用弹性螺旋阵列设计超表面[148,149],沿着轴向拉伸螺旋阵列可以控制带隙,从而用于设计新型声学开关.Bok等[150]设计了一种厚度只有1/100波长的声学超表面,该超表面由一组超原子组成,每个超原子包含一组膜和一个充满空气的空腔,可以实现水-空气高效率传声.利用声学超表面相位补偿方法,可以实现声学隐身斗篷[151−153],这种斗篷设计简单,损耗小,具有一定的应用前景.

利用亚波长厚度的超表面实现高效率吸声具有广泛的应用前景.Ma等[154]设计了一种基于耦合薄膜结构的声学超表面,并且利用其杂化的共振状态使该结构的阻抗与空气的阻抗匹配,实现对声波的完美吸收.Li等[155]通过耦合不同的谐振器并产生混合谐振模式,设计出在调谐频率下与空气声阻抗相匹配的声学超表面,可以实现511 Hz的中心频率处超过99%的能量吸收.利用多孔超表面和三维单端迷宫式超表面可以实现声波的宽频段高效吸收[156,157]；Jimenez等[158]利用超表面还可以实现完全准全向声吸收.目前研究者们主要关注的是利用超表面实现对低频声的宽频带吸收[159−162].

声学超表面还可以实现对声波的超分辨成像效应[163].由钢制成的星形晶格结构低密度的单相位超透镜[164]有双负参数性质,它可以实现超过衍射极限的声聚焦.Esfahlani等[165]基于声传输线超材料的独特性质并利用声漏波辐射的独特物理行为实现了首个声色散棱镜.Xie等[166]利用二维超材料主动相位阵列作为亚波长像素实现了声学全息成像,避免了设计繁杂的电路,大大降低了系统复杂度,基于超材料的全息图可以作为各种先进的声波操作和信号调制的通用平台.Song等[167]通过替代的方法实现了低损耗和大折射率的声学超材料,利用分形方法在很宽的频率范围内实现了超分辨成像、隧道效应以及出色的平板聚焦效应.

综上所述,由人工超原子或超分子构成的声学超材料和超表面的发展经历了从初始阶段“如何设计单负和双负超材料”到现阶段“超材料与超表面实现对声波的反常调控”的过程,在这个发展过程中,基本单元超原子和超分子具有很灵活的设计空间,这也为声波的调控提供了更多可能性.另外,一些新的方法和理念(如拓扑声学等[168−172])的引入更增加了声波反常调控的可行性和实用性.根据目前的发展趋势,相信人工设计的声学超材料和超表面可以根据人类的需求实现对声波的任意调控,并有望从基础研究向应用领域转变.未来人们有望利用声学超材料和超表面实现医疗上的高清超声成像、水中舰艇的声呐隐身、城市噪声污染的有效控制等.