太阳电池单二极管模型中的参数提取方法∗

肖文波 刘伟庆 吴华明 张华明

1)(南昌航空大学,江西省光电检测技术工程实验室,南昌 330063)

2)(南昌航空大学,无损检测技术教育部重点实验室,南昌 330063)

(2018年5月26日收到；2018年6月25日收到修改稿)

1 引 言

随着经济发展,能源需求越来越大.能源储存的有限问题促使人类去开发、寻找新的替代能源.在世界各国日益重视环境及可持续发展的今天,自然会把目光投向太阳能的光电转换器件——太阳电池[1,2].由于太阳电池生产工艺的差别,导致电池特性存在差异；当多块太阳电池串、并联构成阵列发电时,只有每一块电池片的性能相同,才能高效地发电,否则就会相互影响而降低总体输出功率,严重时甚至会导致太阳能发电系统烧毁[3,4].为此,太阳电池特性的研究是人们持续关注的重点.

太阳电池的特性通常是通过电流-电压测量曲线来确定属性.但是由于电池的强非线性特征,仅仅通过电流-电压测量曲线不足于分析清楚电池特征随外界温度、光强等的变化规律.所以,目前太阳电池的建模及其参数研究是当前研究的热点之一.好的太阳电池模型及模型参数提取方法对于太阳能光伏发电系统的模拟、设计、评估、控制和优化至关重要[5−7].一个合适的太阳电池模型及参数估计方法应具有以下特点[8]:1)模型及参数描述不同电池的特征信息时应清晰、完善,应具有适应性；2)运用模型及参数反演的电流-电压数据应接近实验数据或数据表信息,应具有正确性；3)多次运用模型提取一个特定电池数据表中电池参数时,获得的结果应该非常相似,应具有可重复性；4)运用模型及参数分析电池特征时,应计算时间较少.尽管现在已经有大量的研究工作来解决太阳电池模型及其参数估计问题,但仍有研究工作在着力有效地解决这个问题.

目前,用于描述太阳电池特征的模型,包括单二极管模型[9]、双二极管模型(两个二极管并联)[10]以及三二极管模型(三个二极管并联)等[11].不同的研究指出,双、三二极模型比单二极管模型更能准确地反映太阳电池的特征,特别是在低太阳辐射下[12,13].虽然双、三二极管模型是比较准确的模型,但是由于这两个模型更复杂且它们的参数是以非线性方式定义的,所以其附加的困难和较长的计算时间也体现在方程上.因此当前单二极管模型是最受欢迎的模型,原因不仅是该模型比较简单,更是由于大多数情况下它几乎与双、三二极管模型一样准确.单二极管模型是Shockley[14]在1949年以电流连续性特征为基础首先提出的,此后Kammer和Ludington[15]在1977年运用电流密度特性重新描述该模型.它只有五个参数:1)光生电流(或称为感应电流),是指电池在光照下,光生载流子的移动所产生的电流,它与电池能带、光生载流子的产生率及迁移率密切相关；2)二极管反向饱和电流(或称为暗电流),与电池PN结中势垒高度、耗尽层宽度以及器件的温度有关；3)二极管理想因子(或称为发射系数),是电池中缺陷对光吸收和发射影响的量度,理想因子值越大,电池中复合越严重；4)串联电阻,主要来源于半导体材料的体电阻以及金属与半导体材料之间的接触电阻；5)并联(或称为分流)电阻,体现电池PN结的非理想特性和结附近杂质造成的局部短路特征.这些参数包涵深刻的物理含义,不仅与电池的材料、工艺等密切相关,而且能够解释外界遮荫等的影响规律[16],所以它们十分重要；但上述参数需要根据电池的测量电流-电压数据来确定和提取,而不能直接获得.

太阳电池单二极管模型的基本结构是由恒流源、二极管、并联电阻和串联电阻组成,如图1所示.在恒定光照下,太阳电池特性的电流输出方程(或者电流密度输出方程)表述如下:

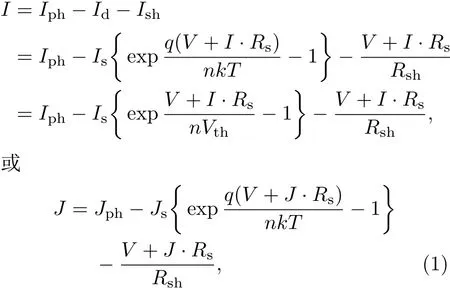
式中I是负载上电流,Iph(Jph)是光生电流(光生电流密度),Id是二级管上电流,Ish是并联电阻上电流,Is(Js)是二极管反向饱和电流(二极管反向饱和电流密度),q是电子电荷常数,V是负载上电压,Rs是串联电阻,n是二极管理想因子,k是玻尔兹曼常数,T是测试时电池温度,Rsh是并联电阻,Vth(=kT/q)是结电压.

图1 太阳电池单二极管模型的电路Fig.1.The equivalent circuit of solar cell’s single diode model.

由于(1)式为非线性超越方程,对Iph,Is,n,Rs,Rsh五个参数不能直接给出解,因此得到以上五个参数的方法就是拟合实验数据.目前提取模型参数的方法,大致分为解析提取参数方法、利用特殊函数提取参数方法等.解析提取参数方法就是通过做一些近似或简化的假设或通过忽略一些模型参数或为某些参数指定一些近似值,来建立五个代数方程求解上述参数[17,18].还有利用特殊函数化简(1)式提取参数的方法,例如用Lambert W函数的方法[19].还可以通过智能迭代算法来确定电池参数[20−23]或者使用曲线拟合技术提取电池参数(通常使用最小二乘曲线拟合法),具体就是通过最小化I-V曲线和测量曲线之间的差异来确定模型参数[24,25].此外,还有利用上述一些方法的混合理论[26,27]提取电池参数等.下面对涉及参数提取中的四类典型方法进行详细阐述,即解析提取参数方法,借助朗伯W函数(Lambert W函数)提取参数方法,构建或利用特殊函数提取参数方法,利用智能算法提取参数方法.每类方法中以四个例子的特点展开说明,分析其优缺点.最后,总结并展望了未来电池参数提取的发展动态.

2 解析提取参数方法

解析提取参数方法是通过特定的I-V特性值(例如短路电流、开路电压、最大功率处的电流和电压等),在假设一些条件的基础上,依据五个测量值,将(1)式转化为封闭代数方程组,然后联立计算得到电池参数.下面对涉及此类方法的四个例子进行介绍.

1)采用电池短路、开路情况及任何其他点的斜率(即导数dI/dV)提取参数的方法

一个名为“Five Points”的参数解析提取方法构建五个方程的步骤如下[28]:首先以短路电流、开路电压和最大功率点三点构建三个方程；其次,通过使用短路电流与开路电压的斜率近似值作为条件,构建两个方程；最后,由上述五个方程求解出电池五个参数.五个参数的解如下:

式中Isc,Voc,Im和Vm分别为电池短路电流、开路电压、最大功率点处的电流和电压；

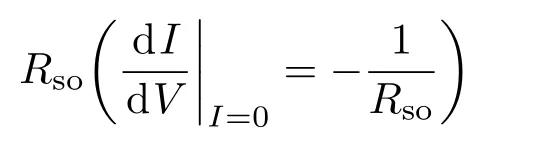
是开路电压处的串联电阻,

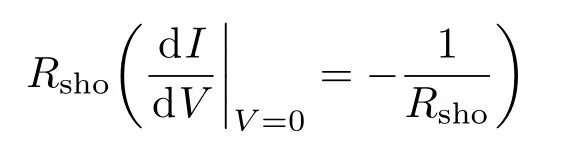
是短路电流处的并联电阻；其他参数如上所述.类似的方法还有文献[29]提到.

2)采用电池短路与开路情况、最大功率点的特征及电池温变特性提取参数的方法

与上面方法类似,构建的五个方程中首先以短路电流、开路电压和最大功率点三测量数据构建三个方程.其他的两个方程分别为:第一个方程是根据最大功率点处,功率对电压导数为零的特征建立；另外一个方程是基于开路电压随电池温度的变化关系得到[30],如(7)和(8)式所示:

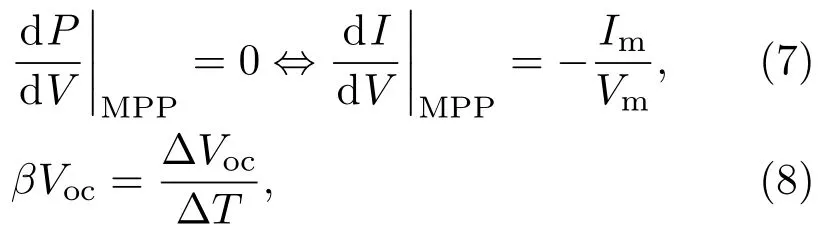
式中P是电池功率,MPP是最大功率点,∆Voc是开路电压的变化,∆T电池温度的变化,β是电池温升系数；其他参数如上所述.

实际上,(8)式指出开路电压与电池温度呈线性变化规律；文献[31,32]研究结果表明这通常是有效的,至少在接近25◦C温度范围内是对的.

3)利用电池电导特性提取参数的方法

为了减少电池五个参数同时提取的难度,并减少光生电流参数在提取中的影响,有研究对电池I-V特性曲线进行求导后,分析得出电池五个参数[33].具体为:正向偏压下,由于V+RsI≫kT,由(1)式的求导,可得

式中G(=dI/dV)是电流对电压的导数,其他参数同上述.

为了进一步验证文献[33]所提方法的正确性,作者与文献[35]提取的电池及组件参数进行了对比,具体结果见表1.从表1可以看出,两种方法提取结果总体相同.但作者研究表明文献[33]的计算精度远高于数值方法.原因在于使用小的电压步长(通常小于1 mV)可以获得高精度的电导数据等,从而降低噪声的影响.类似的方法文献[36]也有提及.

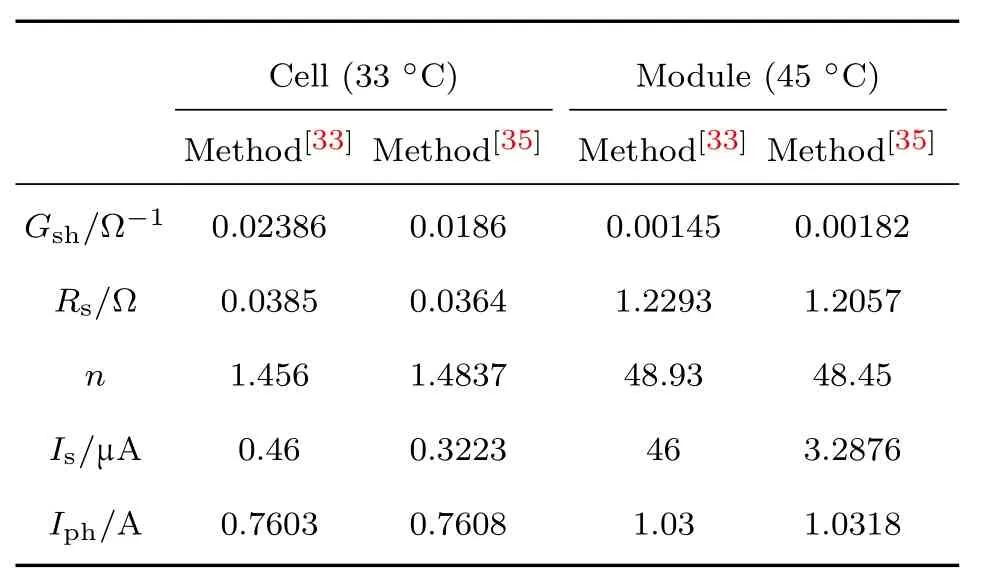
表1 文献[33]与文献[35]提取的电池及组件参数对比Table 1.Obtained parameters in Ref.[33]and Ref.[35]for both the solar cell and the module.

4)利用厂商数据表值来估算参数的方法

首先依据厂商数据表中标称二极管反向饱和电流与光生电流,基于光强、电池温度、电池材料能带、电池电流温度系数的数据,求解出反向饱和电流与光生电流,具体如(10)和(11)式所示.然后利用开路电压、短路电流、最大功率点电流及电压,求解出电池串联电阻、并联电阻[37].最后,找到参数理想因子的方法是将其值从0逐渐递增,直到并联电阻值变为负数.因此,理想因子的实际值为并联电阻处于最小正值时.

反向饱和电流与光生电流的求解方程如下:

式中Isn,Tn,Eg分别是标称二极管反向饱和电流、标准电池测试温度、电池的材料能带；S,Sn,Ipvn,Ki分别是电池受到的辐射强度、标准电池测试辐照强度、标称电池光生电流、电池电流温度系数.其他参数如上述.

该研究与文献[38,39]中所提方法进行误差对比,发现该方法小于5%,而文献分别达到12%与25%.显然,这里参数提取精度提高了.当然,由(10)和(11)式也可以看出,该方法参数提取精度与厂商提供的标称数据准确度密切相关且受电池温度估算的热模型影响较大[40].

由上述解析提取参数方法中四个例子的分析,可以看出该类方法是基于简单的公式,所以求解五个方程的思路清晰且执行起来很快；但在处理电池的非线性特性时,引入了假设和简化,由此导致该类方法注定精度不会太高.此外,可以看出该类方法建立的方程需要利用I-V特性曲线上的选点,由此选点处的正确性必将影响提取出的参数精度,而选点处数据往往会受噪声影响而波动.

3 借助Lambert W函数提取参数的方法

提取电池参数中使用Lambert W函数的方法,是Jain和Kapoor[41]在2004年首次提出,该方法的特点借助于Lambert W函数的帮助,将(1)式化简得到显示表达式,然后结合电池短路电流、开路电压和最大功率点及上述三点的斜率,提取电池五个参数.随后有各种改进方法被提出,下面对涉及此类方法的四个例子进行介绍.

1)借助于Lambert W函数的帮助,得到只依赖于理想因子、串联电阻和并联电阻的表达式；然后直接用表达式来拟合实验数据并提取电池的参数[42].

在Lambert W函数的帮助下,(1)式可表示为

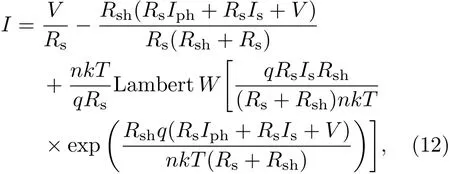
式中参数如上所述.(12)式仍然不适合用于提取器件参数.当它被直接用在曲线拟合来提取电池五个参数时,将会产生非常大的误差.这主要是由于Is和Iph值之间有非常大的差异,它们的值之间的差通常大于6个数量级.因此,方程(12)必须处理好后方可用于电池参数提取.

在电池短路和开路情况下以及假设条件

下,方程(11)被化简为

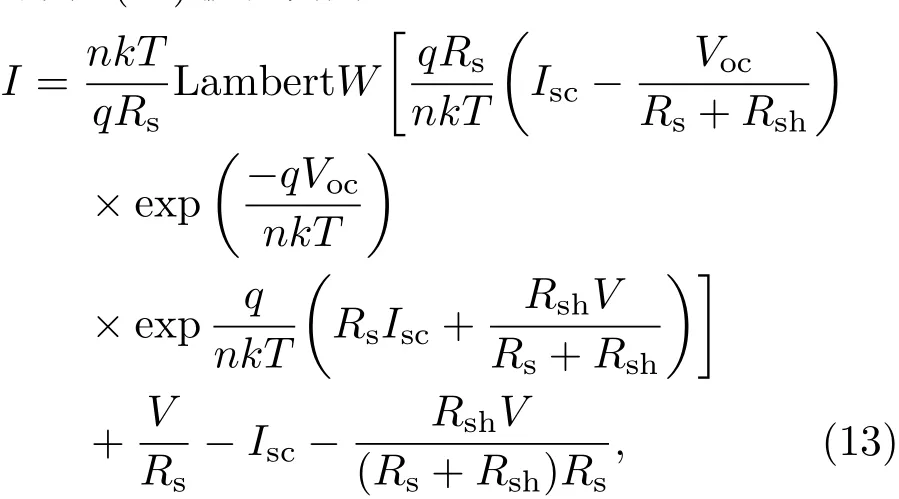
式中参数如上所述.(13)式适合于通过非常成熟的最小二乘法提取n,Rs和Rsh参数.

提取n,Rs和Rsh后,Is和Iph值可以根据(14)和(15)式来计算:

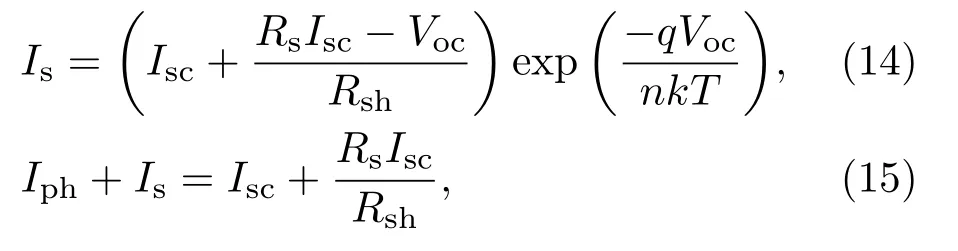
式中参数如上所述.

最小二乘法拟合提取参数时,需要n,Rs和Rsh的初始值.获取方?式如下:在短路情况得到R初始值,即sh在开路情况得到n,Rs的初始值,即根据变化的斜率与截距得到.

文献[42]作者利用上述方法提取的参数重建I-V曲线,并与文献[36]对比；发现该方法得到的曲线与实验数据符合度提高了.类似的方法还有文献[43]提到,只是该方法是通过短路电流与开路电压处斜率提取参数初始值.

2)上述使用Lambert W函数显化电池电流电压关系时,是以电压为自变量,电流为因变量.Ghani等[44]提出相反的思路来提取电池参数,如此(1)式可表示为

式中参数如上所述.

Ghani等这样变换的目的,在于电压受外界噪声影响比较容易控制,数据测量更精确.建立五个方程的选点是从实验I-V数据中短路、开路和最大值附近选取.此外,迭代计算五个参数中,使用前面讨论的分析来近似获得每一个参数的初始值；简单如假设理想因子约为1[45],光生电流约等于短路电流等.

3)从上述可知,使用Lambert W函数求解参数时,初始值的选择非常重要.文献[46]在Iph≫I0,Iph+I0≈Iph,Iph≈−Isc及Rsh≫Rs假设下,利用电流电压方程的一阶以及二阶微分方程得到n,Rs和Rsh初始值；然后代入基于Lambert W函数的显化解中,用最小二乘法求出n,Rs和Rsh；最后,代入短路电流与开路电压点计算Is和Iph.

n,Rs和Rsh初始值是联立(17),(18),(19)三个方程获得:

式中参数如上所述.

该文作者利用一阶以及二阶微分方程求解初始值的目的在于,一阶以及二阶数据的精度更高.

4)由于实验测量数据的精度对提取电池参数的精度有很大的影响,由此Chen等[47]提出用多项式曲线拟合技术和Lambert W函数相结合提取电池参数；原因在于多项式拟合技术可以克服测量噪声对实验数据的影响.

Chen等的具体做法为,借助Lambert W函数,微分方程dV/dI表示为

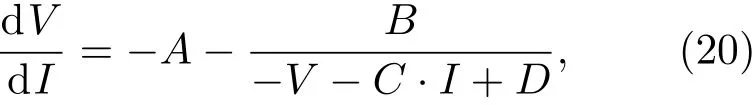
式中A=Rs,B=nVthRsh,C=Rs+Rsh,D=nVth+Rsh(Is+Iph),有四个未知参数A,B,C和D.

为了求解上述一阶微分方程中四个参数,实验I-V曲线被分割为三阶多项式拟合公式；通过对比(20)式与三阶多项式拟合公式之间的关系,求解出A,B,C和D；然后确定Rs,Rsh,n和Iph+Is=Z；最后,Is和Iph通过下面公式得到:

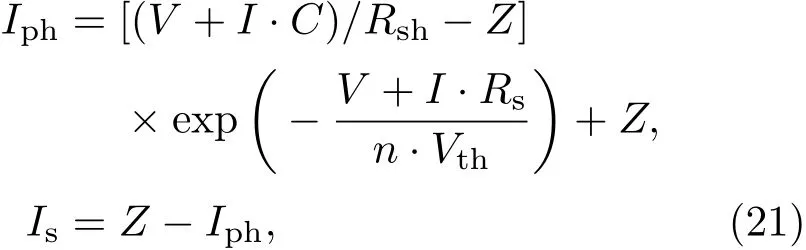
式中参数如上所述.类似的方法还有文献[48]提到.

与解析提取参数方法对比,借助Lambert W函数方法可以将(1)式化简得到显式表达式,求解得到电池参数精度较高；但也是存在缺点,例如每个参数的初始值需要选择以满足迭代求解过程以及增加了执行数值算法所需的计算时间等.

4 构建或利用特殊函数提取参数方法

构建特殊函数提取参数方法就是建立新的太阳电池物理形式,并与电池单二极管模型对应,提取出电池理想因子等五个参数.利用特殊函数提取参数方法就是通过特殊函数,变换电池超越方程的形式,求解出五个参数.下面对涉及与此类方法的四个例子进行介绍.

1)Saleem和Karmalkar[49]提出的幂律物理形式

幂律物理形式是指光照下太阳电池的J-V曲线用显式幂律函数表示:

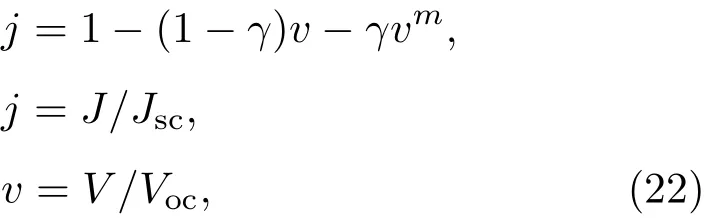
式中γ和m为系数,可以从V|J=0.6Jsc,J|V=0.6Voc两个数据点计算得到；Jsc和Voc分别是短路电流密度及开路电压；其他参数如上述.

上述物理形式与单二极管模型对应后,可以得出五参数,如(23)—(27)式:

式中vp≈(m+1)−1/m−0.05(1−γ)；其他参数如上述.类似的方法还有文献[50]提到.

2)使用特殊反式函数理论(STFT)解(1)式超越方程[51]

利用tans+(D)函数[52],(1)式超越方程的解有如下形式:

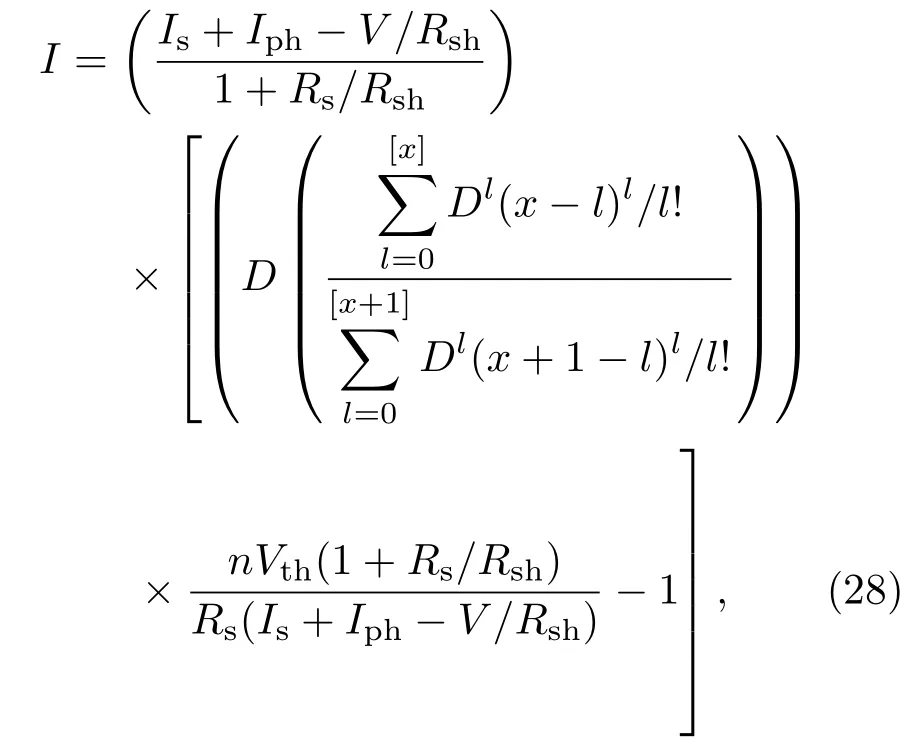
式中[x]为测量数据的最大整数,l是变量；其他参数如上述.

利用上面类似方法得到初始值后,采用(28)式就可以拟和实验数据求解出电池理想因子等[53].表2是文献[51,54]获得的蓝与灰电池理想因子对比.从表2可以看出,由STFT法得到的理想因子比由Lambert W函数方法[54]提取精度明显提高.实际上,特殊反式函数理论是一种新的理论,它不涉及近似,给出了电池超越方程的显式解.显然,该方法具有较高的计算精度,且具有较小的计算量和计算时间,给出的技术路线相比Lambert W函数方法更占优.

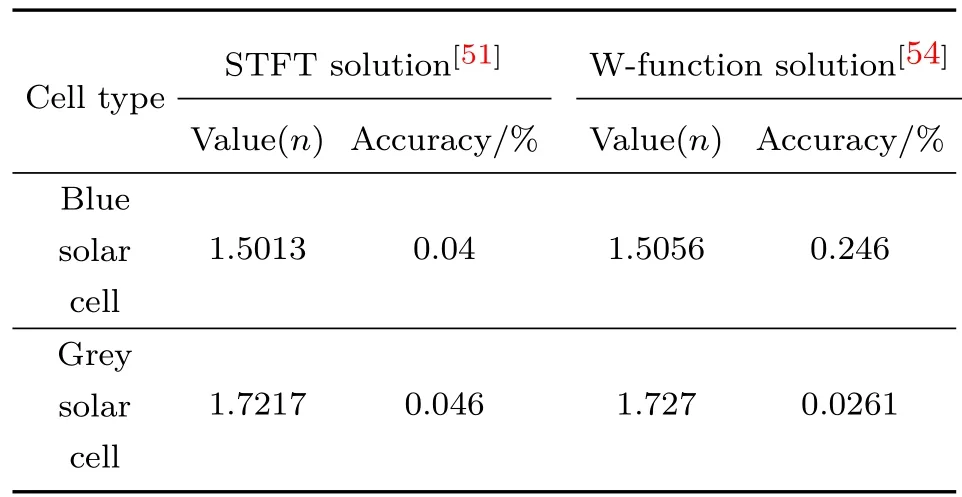
表2 文献[51]与[54]获得的蓝与灰电池理想因子对比Table 2.Ideality factors obtained by different methods for blue and grey solar cell.

3)构建只有三个参数的紧致物理形式[55]

有研究提出了只有三个参数的紧致物理形式来描述电池特性,然后采用对应函数提取电池五个参数,紧致物理形式为:

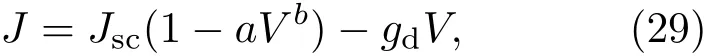
式中a,b,gd是紧致物理形式中的参数；线性项gd×V表示电池并联电阻和功率大小对其性能的影响；a×Vb反映了电池空间电荷的漏电流、隧道电流等.式中其他参数如上述.

根据I-V实验数据,确定(29)式中物理形式参数；然后对应单二极管模型就可以得到电池五个参数.例如串联电阻为:

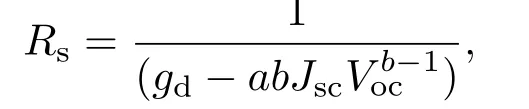
式中参数如上所述.与其他复杂隐式函数相比,紧致物理形式不需要数值迭代.

4)构建只有二个参数的电池特性表达式[56]有研究提出了只有二个参数的电池特性表达式:

式中A与B是方程的参数；其他参数如上所示.

该研究首先利用Levenberg-Marquardt算法、高斯-牛顿算法、差分进化算法(这些算法是求解非线性最小二乘问题的最标准技术)使得理论数据点与测量数据点之间的误差最小,寻找出A与B参数值；然后,对应(1)式求到电池五个参数.类似的还有Akbaba和Aiattawi[57]建立的电池特性表达式,为J=(Voc−V)/[(Voc/Jsc)−CV+DV2],其中C与D是方程参数.其他还有借助Green函数等[58]数学公式来提取参数,但这是一个更复杂的方法.

构建或利用特殊函数提取参数方法,本质上是提出先验的电池特性封闭形式解或利用特殊函数求解出电池方程的形式解.该类方法避免了任何斜率点数据的测量,相对精度较高.显然,该类方法提取参数的精度受限于特殊函数是否能够合理并准确地描述电池输出特性.

5 利用智能算法提取参数方法

考虑到太阳电池发电具有强非线性属性,电池参数也随外界环境等迅速变化,有研究提出一些仿生的、随机的概率搜索方法来提取电池参数[59−61].基本思想是以迭代的方式操作,使实验与理论值最小化提取电池五个参数,例如粒子群算法、遗传算法和差异演化算法等.下面对涉及此类方法的四个例子进行介绍.

1)遗传算法用于电池参数提取[62−65]

为了数值处理I-V实验曲线,有研究执行了一个基于遗传算法的理论拟合来提取电池参数.拟合过程中所采用的误差准则是基于理论值和实验值之间的平方差之和最小[66].设置的最小化函数是由(31)式定义:

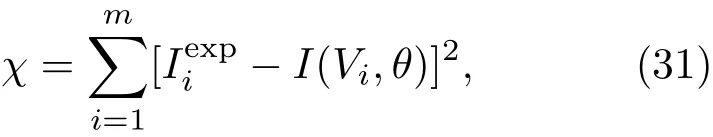
遗传算法用于电池参数提取的基本过程是:定义参数及最小化函数,创造种群并初始化,评估最小化函数,遗传操作(选择、交叉、变异)生成新种群,测试收敛性能,得到五个参数的最佳值.遗传操作中三个方面的意义分别是:1)选择,此过程用于选择染色体,只有最好的染色体保留为下一代,而坏的则被丢弃,选择的目的是把优化的个体直接遗传到下一代；2)交叉,此过程需要两个当前世代的选定染色体与它们杂交而获得两个新个体；3)变异,对群体中某些基因座上的基因值做变动或引入一些变化.

实际上,上述从实验数据中搜索出光生电流等五个参数是以非凸优化问题的形式提出来的.传统的非线性规划技术解决这个问题,如Newton Rafson算法,处理并不好,因为它们取决于导致局部最优解的初始条件影响.而遗传算法可克服这个问题,但是,遗传算法也存在不足之处[67].首先,当使用高本源性目标函数时,即当被优化的参数高度相关时,搜索效率低.其次,交叉和变异算子并不总能保证后代具有更好的适应性,因为种群中的个体具有相似的结构,并且在进化过程结束时其平均适应度较高.再次,在多变量优化问题的情况下,遗传算法具有陷入局部极小值而不是全局最优的趋势,这可能是由于交叉和变异概率选择不当所致.最后,对这类算法的搜索速度适当优化是非常繁琐的,而且依问题而变得十分复杂.

2)粒子群优化算法用于电池参数提取[68,69]

粒子群算法源于对群体性鸟类寻找食物行为的模拟,假设鸟群中的每只鸟都不知道将要寻找的食物的具体位置,而食物的位置是随机的,最初寻找食物是鸟群都是分散的；而当一只鸟找到食物所在的位置时所有的鸟就会迅速地聚集在某一点.若将一只鸟都当作粒子群算法中的一个粒子,每个粒子都有其自身的位置、速度和适应度函数.找到食物鸟的位置,即是粒子群算法要求出的潜在最优解.

Ye等[70]提出的粒子群算法流程如下.

第一步,初始化粒子.首先初始化粒子群算法中各个参数的数值,包括种群规模、学习因子、惯性权重、迭代次数或者收敛精度、搜索空间的维数、粒子的初始速度以及位置等.

第二步,评价粒子.由适应度函数计算出粒子的适应值,比较出群体中的个体最优值pbest和全局最优值gbest,再把当前迭代后各粒子的适应值以及位置存储于各个粒子的个体最优值中,把所有个体最优极值中适应值最优的粒子的位置以及适应值存储于全局最优值中.

第三步,更新粒子.根据公式更新粒子的位置和速度,如果粒子的速度和位置超出设置的上下限则将其设置为上限或者下限.

第四步,重新计算最优值.重新计算粒子的适应度值并和之前的比较,更新个体最优值与全局最优值.

第五步,检验是否终止.如果搜索结果达到收敛精度或者是设定迭代次数,那么迭代终止并输出最终解.如果不满足,就跳转至第三步继续迭代计算.

可以看出,粒子群优化算法有两个方面优于遗传算法:1)它不像遗传算法那样,需要二进制编码的转换和特殊遗传算子；2)粒子群优化算法不受遗传算法中复杂计算的影响.但粒子群优化算法也有缺点[71]:1)不能保证提取参数的一致性；2)需要大量迭代才能将解收敛到全局最优.

3)基于教学的优化算法用于电池参数提取

近年来,Rao等[72]提出基于教学的优化算法用于电池参数提取,该方法是模拟了教师给学员的教学过程和学员的学习过程,目的是通过教师的“教”和学员之间的相互“学习”来提高学员的学习成绩.基于教学的优化算法具有参数少、算法简单、易理解、求解速度快、精度高且具有极强的收敛能力等特点.下面以Patel等[73]提出的基于教学的优化算法进行阐述,算法的详细流程如下.

(a)初始化班级

(b)“教”阶段

采用如下方法实现“教”的过程,“教”完成后,更新学员.学习的方法是寻找教师Xteacher和学员平均值之间的差异性,公式如下:

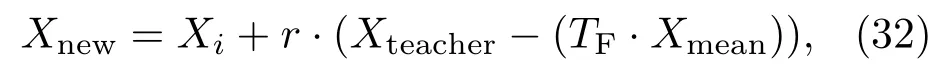
式中Xi,Xnew表示第i个学员学习前和学习后的值,r是学习步长；Xmean是所有学员的平均值,TF是教学因子.

(c)“学”阶段

采用如下公式实现“学”的过程,“学”完成后,更新操作.公式如下:

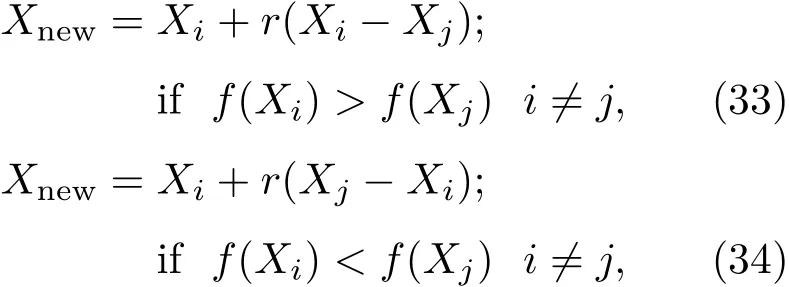
如果Xi比Xj好,那么Xj移向Xi,如(33)式；否则,如(34)式.只有在Xnew比Xi优,那么Xi被Xnew替代.

(d)如果满足结束条件,则优化结束,否则转至(b)继续.

已经证明,基于教学的优化算法可以解决大范围的全局优化,可以用少量的控制变量实现与最初种群数量无关的全局最优解.

4)基于神经网络的电池参数识别方法

首先利用人工神经网络提取电池参数的是Singh等[74]；事实上,他们的研究发现,通过多输入多输出神经网络直接提取电池五个参数是一项非常困难的任务.其后有研究利用神经网络的泛化能力结合单二极管模型的简化形式提取电池参数[75].简化形式是指一系列明确的解析公式.该研究只是利用神经网络提取电池五个参数中的两个,其他三个参数是用简化形式(即封闭形式解析方程)计算得到.从计算成本和参数估计准确度的角度来看,这种五个参数的混合提取方法是有效的.

提取方法的流程为:根据Voc,Isc,VMPP,IMPP,,(,分别短路电流温度系数以及开路电压温度系数)输入神经网络,提取出电池串联电阻和理想因子[76].然后,利用上述值和电池短路电流、开路电压、最大功率点电流和电压等代入封闭方程组,解得其他三个参数.上述类似的方法还有使用全局搜索的细菌觅食算法[77]、基于猫群优化算法等[78].为此,有人对比研究了六个生物优化算法,即遗传算法、差分演化算法、粒子群优化算法、细菌觅食算法、人工蜂群算法和杜鹃搜索算法,结果表明,杜鹃搜索算法在这些生物启发优化算法中更加鲁棒和精确[79].

一般而言,利用智能算法提取参数的方法虽然具有精度较高的特点,但都对控制参数高度敏感[80]；所以往往由于缺乏准确的初始条件而导致不能收敛[81].例如:与粒子群优化算法相关的主要缺点是早熟收敛和种群多样性的损失等[82].实际上,各种算法提取电池参数的本质,是并行、随机、有一定方向的搜索方法.算法中新解的产生机制和接收机制对于搜索中全局收敛能力十分重要,有助于克服局部最优问题.尽管各种算法都有其优点,但不可否认缺点也很明显,这里涉及到有效初始参数的设置、迭代停止条件等.所以,目前研究还是结合各种算法的特点,开发新的搜索理论研究才是重点.

6 总结与展望

近年来,太阳电池单二极管模型参数的提取方法涌现出了各种不同的新理念、新思想,从不同角度对提取精度与速度进行了深入研究,取得了令人瞩目的丰硕成果.然而,面对电池参数提取问题仍然有下列值得深入研究的内容:1)针对不同的电池特性,提出可以快速且高精度的电池参数提取方法,原因在于不同电池如染料敏化电池、硅电池等具有各自的特点,有针对性的电池参数提取方法可能更好；2)针对非线性方程迭代求解中,发展并完善合适的初始值选择方法,比如通过特殊函数来甄别初始值,这样既可以避免局部最优提高全局搜索能力,也可以提高搜索速度.此外,实现高效的参数提取方法中结合现有方法的优点,发展混合方法的方向也是一个好的思路.当然,也需要更多地关注材料的基本性质和电池工作原理的深入研究和理解,这能为人们寻找更简单的方法提供基础.