一维扩展量子罗盘模型的拓扑序和量子相变

陈西浩 王秀娟

1)(重庆大学材料科学与工程博士后流动站,重庆 400030)

2)(重庆大学,输配电装备及系统安全与新技术国家重点实验室,重庆 400044)

3)(重庆大学物理学院,重庆 400044)

(2018年4月30日收到；2018年7月13日收到修改稿)

1 引 言

量子多体系统的量子相与相变一直是凝聚态物理研究的重要内容,尤其是自朗道自发对称破缺相变理论诞生以来,为了获得更多物相本质,人们引入了大量的理论模型.扩展的量子罗盘模型[1](quantum compass model,QCM)就是其中非常重要的一个.该模型可以描述过渡金属氧化物的电子输运特性和量子比特保护机制,特别是量子比特保护机制在量子信息技术中存在潜在应用[2,3].因此该模型的相图本性得到了广泛的研究.人们使用了多种解析和数值模拟方法对存在和不存在横场的QCM进行了研究[4−16].文献[4—7]的结果表明:模型相变是系统内在引起的且两个无序相间是非连续相变；Sun和Chen[8]的自旋-自旋关联、保真度磁化率和块纠缠熵的有限尺寸标度研究结果支持连续相变的观点；而后Wang和Cho[9]的结果也支持这个观点；文献[10,11]综合了前两种观点,认为连续相边界与非连续相边界交叉处是多临界点.特别地,Su等[11]对该模型进行了全面的研究,得到了全面可信的结果(包含:能量、关联、纠缠、纠缠谱简并度、保真度、序以及临界指数).目前对于该模型的研究,人们把大量的精力都放在了相边界上,却鲜有人关注非局域长程拓扑弦关联序参量(以下简称弦关联序参量).本文在文献[11]的基础上,借助矩阵乘积态表示的无限虚时间演化块算法[17],详细地展示了如何从奇偶数弦关联导出弦关联序参量来研究该模型的量子相与相变的过程.要研究序参量,首先要明确的是序参量的概念.按照朗道自发对称破缺理论的理解,可以表述为:当系统发生自发对称性破缺时,系统就会存在一个局域序,而这个局域序可以用一个局域序参量来刻画[18].该序参量可以将局域相和其他相区分开,对于连续相变还应满足标度定律.然而长程拓扑相是一类新颖的相,超越了朗道连续相变理论,无法使用传统的Landau-Ginzburg-Wilson范式的两个基本概念:自发对称性破缺与局域序参量.但我们可以借助序参量的概念来定义弦关联序参量.局域序参量一般是根据局域磁化强度来确定的.弦关联序参量的定义可以参照以上思路,用弦关联来定义,需满足:1)系统需发生隐性对称破缺；2)该弦关联序参量可以唯一刻画区分对应的长程拓扑相区域；3)对于连续相变,在相变点附近满足标度定律.

本文第2部分介绍了模型与相图；第3部分应用单位格点保真度重复确认了相图；第4部分详细介绍了如何导出弦关联序参量的过程,获得了序参量相图并提取了临界指数；第5部分是总结.

2 模 型

扩展的QCM模型的哈密顿量如下:

图1 扩展的量子罗盘模型示意相图Fig.1.Schematic phase diagram of the one-dimensional extended quantum compass model.

3 保真度

保真度是源于量子信息的概念,用于测量两个量子态的相似度；定义为两个量子态波函数的交叠.在矩阵乘积态表述下,保真度可定义为与控制参量J1和对应的波函数|ϕ(J1)⟩和|ϕ(⟩的交叠,即F(J1=|⟨ϕ(J1)|ϕ(⟩|；其满足：1)归一性F(J1,J1)=1；2)有界性0 6 F(J1,6 1；以及3)对称性F(J1,=F(J,J1).此外,保真度和系统尺度L存在如下标度[20]:

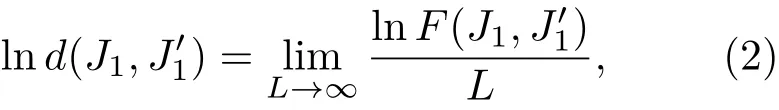
d(J1,)是单位格点保真度.这个定义近年来被引入到量子相变的研究,它能准确而方便地给出相变点位置[20].

在图2中,我们计算了棕色线(1)J2=2(1−J1)上的参数区间的保真度.保真度平面存在两个挤点(相变点),图2(a)在(J1=(0,0)发生非连续相变；非连续相变的传统解释是存在能级交叉,一阶导数不连续,则判定系统发生了非连续性相变.从单位格点保真度的角度而言,保真度表面存在着跳跃(不连续)即判定为非连续相变.出现这种跳跃的原因在于波函数内部结构严重的不一致.图2(b)在(J1=(0.5,0.5)发生连续相变.连续相变的传统解释是能量的一阶导数连续,而二阶及以上导数不连续,则判定系统发生了连续相变.而单位格点保真度则认为只要保真度表面是连续变化的,就认为系统发生了连续相变.发生这种相变的原因在于:系统波函数的内部结构是连续变化的,变化的程度相对远远弱于非连续相变的情况.以上单位格点保真度结果和文献[11]结果一致.

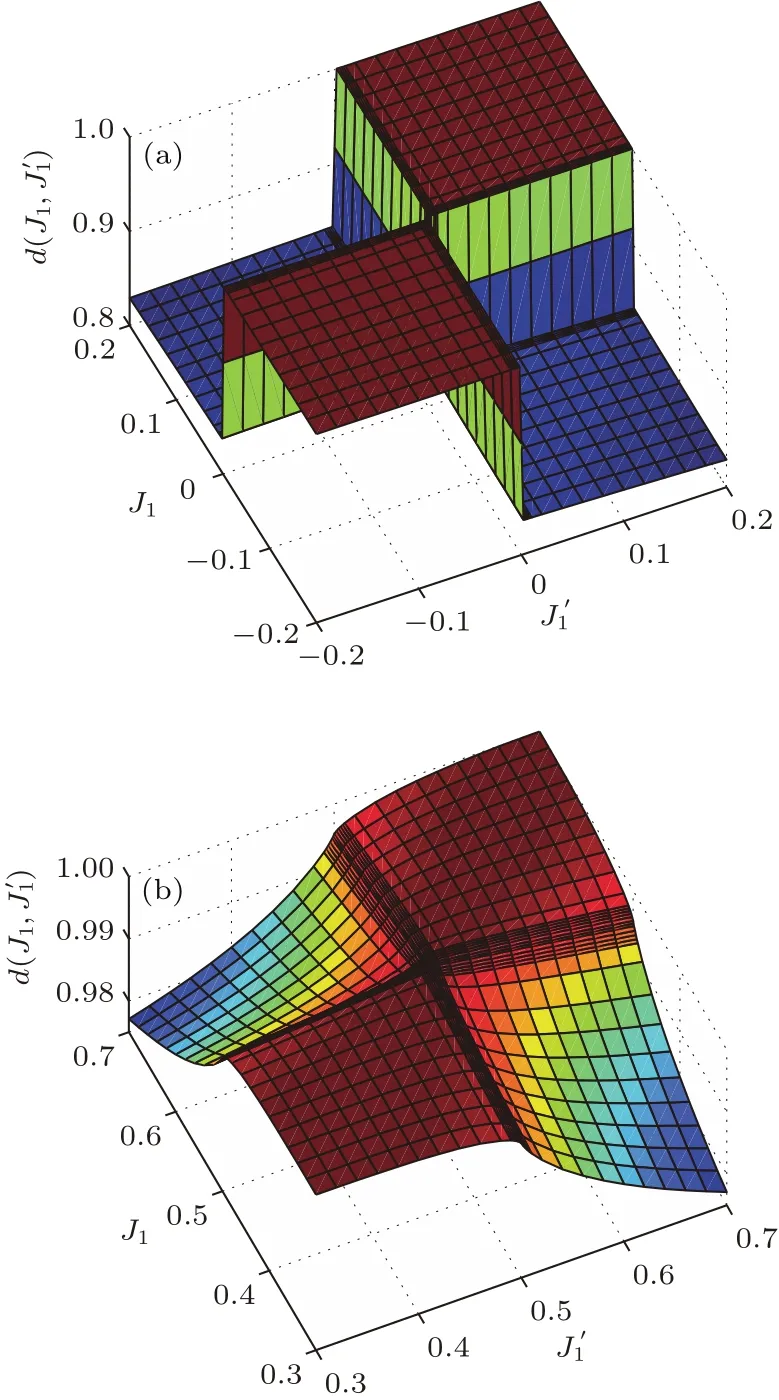
图2 单位格点保真度d(J1,随控制参量J1和的变化(a)非连续相变,在(J1,=(0,0)处；(b)连续相变,在(J1,=(0.5,0.5)处Fig.2.Ground-statefidelity per lattice site d(J1,as a function of control parameters J1and(a)discontinuous phase transition at(J1,=(0,0)；(b)continuous phase transition at(J1,=(0.5,0.5).

4 弦关联与量子相变

扩展的QCM模型的自旋耦合强度取决于轮换的奇偶数键,奇偶数键上耦合强度的不同会体现在基态波函数的奇偶数键的纠缠的不同,奇偶数键纠缠的不同必然导致所有格点有“二聚化”[21,22]偏向,奇数和偶数格点就会有差异.基于此,我们假设奇偶数弦关联函数可以用来区分长程拓扑相,并采用了如下弦关联函数定义[9,23−28]:

4.1 偶弦关联行为

在图3中,我们计算了代表点PII、PI和PIV的偶弦关联的短程行为.在x和y方向,PII,PI和PIV的偶弦关联都衰减为0；在z方向,PII和PI的偶弦关联衰减为0,而PIV的偶弦关联表现为单调负值.

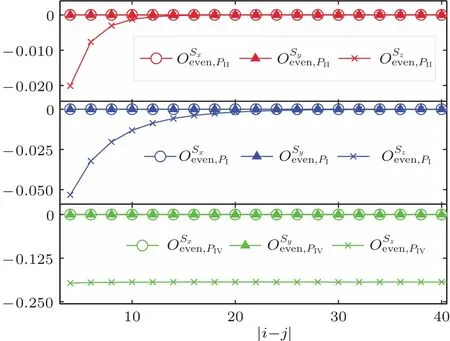
图3 偶弦关联函数O,O和O随格点间距|i−j|的变化行为Fig.3. Even string correlations O,Oand Oas a function of the distance of the lattice sites|i−j|.

4.2 奇弦关联行为

在图4中,类似偶弦关联,我们也计算了代表点PII,PI和PIV的奇弦关联行为.图4(a)点PII奇弦关联O是单调负值,O和O是振荡值.图4(b)点PI的奇弦关联O,O和Osz都是odd单调负值.图4(c)点PIV的奇弦关联O和O非常快地衰减为0,O是单调负值.内插图展示的是奇弦关联的非0长程饱和行为,确保了奇弦关联的非平庸性.自然地,用奇弦关联定义的奇弦关联序参量也就具有了非平庸性.

图4 奇弦关联O,O和O随格点间距|i−j|变化行为,内插图展示的是饱和行为Fig.4. Behaviors of the odd string correlations with the distance of the lattice sites|i−j|.The insets show the saturation behaviors.

4.3 弦关联序参量相图

为了更深刻地理解系统发生的量子相变,需要找到系统的序参量(当系统处于长程拓扑相时应找到弦关联序参量).4.1和4.2节的结果表明:1)偶弦关联,在x和y方向,不管是在长程拓扑相区域还是局域相区域,偶弦关联都衰减为0,这是平庸的,无法用作弦关联序参量的定义;在z方向,在局域相区域里,偶弦关联是单调负值,这和该区域存在明显的局域序相违,所以偶弦关联无法用作弦关联序参量的定义；2)对于奇弦关联,1在x方向,在长程拓扑相区域中都表现出单调负值,在局域相区域,衰减为0；在两个长程拓扑相区域中,偶弦关联行为一致；更为特别的是相图1中的相变点(J1/L,J2/L)=(0,2),和文献[9]中的深度处于长程拓扑序中的点(Jy,Jz)=(8,4)等价,也就是说相变点(J1/L,J2/L)=(0,2)深度处于单调O长程序中,故x方向的奇弦关联在整个长程拓扑区域(含相变点)都具有O长程拓扑序,不可用于弦关联序参量的定义；2在y方向,在长程拓扑相区域II中,奇弦关联表现为振荡行为,即+−+−......+−+−；而在区域I中表现为单调负值,即−−−−......−−−−；在局域相区域IV中衰减为0；3在z方向,奇弦关联一直存在,不可用作弦关联序参量的定义.综上,弦关联序参量仅可采用y方向奇弦关联来定义.结合示意相图特性,可考虑如下两种类型奇弦关联序参量定义:

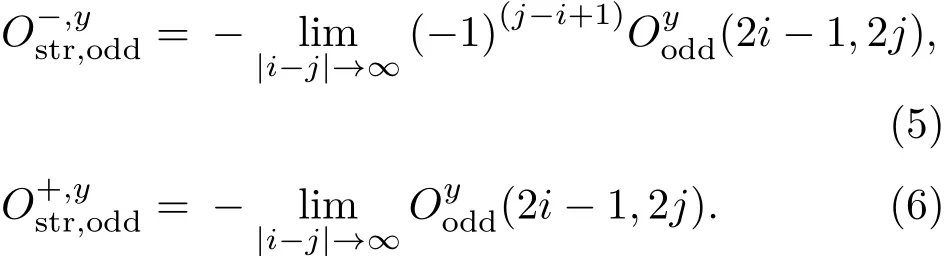
但需要注意弦关联序参量是按照格点间距|i−j|来定义的,理论上来说该间距可做到无穷大,这是有限的时间和计算资源所不允许的,通常人们会设定一个误差范围(本文设定的误差范围是ε＜1e−8),当达到这个误差范围时就认为该弦关联值就是弦关联序参量的值.从相邻相的区分意义上,Wang和Cho[9]成功地找到了一组弦序参量；而弦关联的线性组合弦序参量：

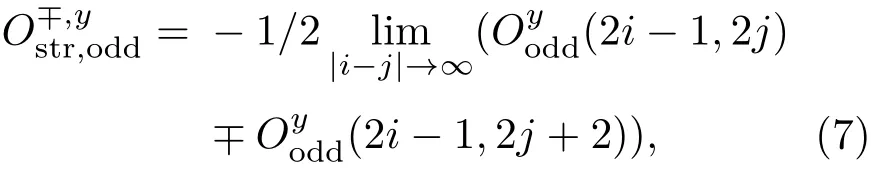
适用于全局参数区间.图5给出了序参量相图,包含y方向的振荡奇弦关联序相(J1＜0)、y方向的单调奇弦关联序相(＜；J1＜0.5)、和反铁磁相(J1＞0.5).单调(振荡)奇(偶)弦关联序参量是Hida等[23]在研究轮换交替作用的海森伯模型时,为了描述偶弦关联Haldane相和二聚相共存的情况而引入.而后Wang和Cho[9]为了刻画区分四种不同的Haldane相而引入到QCM模型中.扩展的QCM模型中虽有轮换交替耦合,却不存在二聚相,但轮换交替耦合确实会导致基态波函数存在“二聚化”偏向.故在引入单调(振荡)奇(偶)弦关联时是假设它们可以用于长程拓扑相区域刻画.经过数值证实,由“二聚化”偏向引入的单调(振荡)奇弦关联序参量可以很好地刻画区分长程拓扑相区域.y方向振荡奇弦关联序参量和单调奇弦关联序参量值非0表明在这两个子区间发生了隐性的Z2×Z2对称破缺.随着控制参量J1增大到0.5后,它打破了原来的长程序,系统发生自发对称破缺,进入反铁磁序.磁化强度表现为符号相反、大小相等.

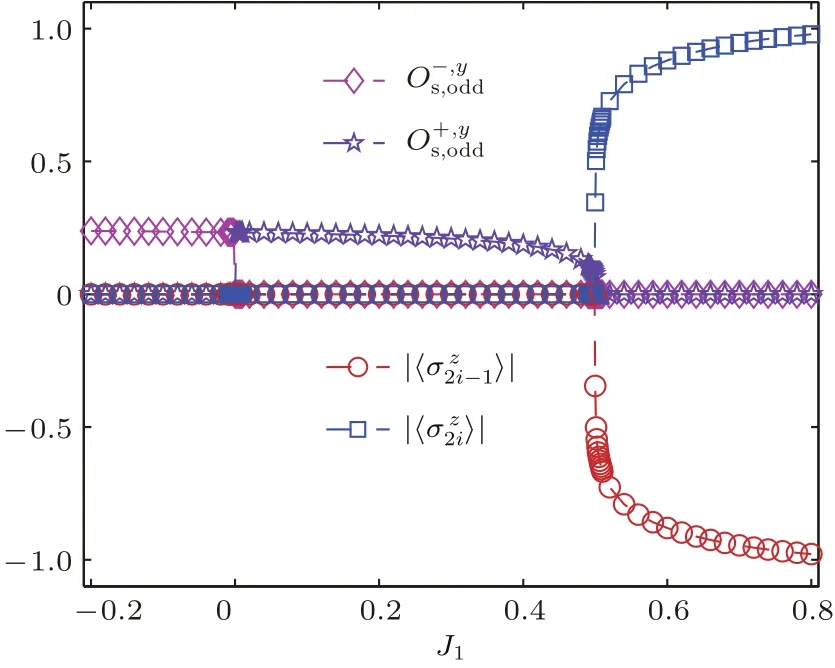
图5 以J1为控制参量的基态序参量相图Fig.5. The ground-state phase diagram of order parameters as a function of control parameter J1.

4.4 临界指数

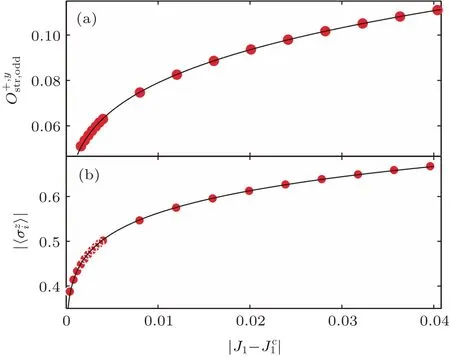
图6 (a)βO；(b) β；图标是数据,实线为拟合曲线Fig.6. (a)β；(b) β.The icons are data.The solid line is fitting line.

临界指数是研究系统临界性质的参数.提取临界指数能从更深的层次上揭示相变的性质.图6展示了渐近临界点J=0.5过程中,y方向的单调奇弦关联序参量和局域磁化强度随着|J1−J|的幂次律变化关系.它们的幂次律拟合方程分别为O=|J1−|2β和|⟩|=|J1−J|β.拟合临界指数βO=0.1236 和β|⟨σ⟩|=0.1246都趋近于准确值β=1/8表明:该处发生相变的普适类为Ising类型.

5 结 论

本文应用矩阵乘积态表述的无限虚时间演化块算法,研究了扩展的QCM模型的长程拓扑相和量子相变.为了深入研究该模型的长程拓扑相和量子相变,按照奇数和偶数键,本文引入了奇数弦关联和偶数弦关联.弦关联表现出三种截然不同的行为:衰减为零、单调饱和与振荡饱和.基于弦关联的以上特征导出的y方向的振荡 (单调)奇弦关联序参量可描述该模型的长程拓扑相和量子相变.y方向的振荡(单调)奇弦关联序参量的非零值表明扩展的QCM发生了隐性的Z2×Z2对称破缺.在临界点J=0.5附近,局域磁化强度和单调奇弦关联序参量的临界指数β=1/8表明相变的普适类是Ising类型.此外,保真度探测到的相变点、连续性与非连续性和序参量结果一致.以上方法对长程拓扑相和量子相变的研究具有指导意义.