2018年高考数列经典问题聚焦

■陕西省洋县中学 刘大鸣（特级教师）

2018年高考对数列主要是围绕“等差和等比数列的通项与求和、一般数列的切入点的应用、累加法与错位相减法求和进而求通项、公式法求和、裂项用公式求和、裂项相消法求和、数列中存在性问题的探究证明以及参数范围的求解”等展开的,凸显了数列的工具性和应用性以及创新性。

聚焦1 等差数列前n项和的最值问题

例1 （2018年全国卷Ⅱ理17）记Sn为等差数列{an}的前n项和,已知a1=-7,S3=-15。

（1）求{an}的通项公式;

（2）求Sn,并求Sn的最小值。

解析：借助等差数列的通项及求和公式构建方程组求通项及前n项和,再用两种思维方法探究等差数列前n项和的最值。

（1）设{an}的公差为d,由题意得3a1+3d=-15。由a1=-7得d=2。所以数列{an}的通项公式为an=2n-9。

变式1 （1）（2018年全国卷Ⅰ理4）设Sn为等差数列an的前n项和,若3S3=S2+S4,a1=2,则a5=（ ）。

A.-12 B.-10

C.10 D.12

（2）（河北衡水中学2018届高三第2次调研）已知数列{an}中,a1=25,4an+1=4an-7,若其前n项和为Sn,则Sn的最大值为。

聚焦2 等比数列的定义、通项及前n项和的应用

例2 （2018年全国卷Ⅲ理17）等比数列an中,a1=1,a5=4a3。

（1）求an的通项公式;

（2）记Sn为an的前n项和,若Sm=63,求m。

解析：可利用等比数列的基本量法构建方程组待定通项,利用求和公式分类待定参数值。

（1）设等比数列an的公比为q,由题设a1=1得an=qn-1。由a5=4a3得q4=4q2,解得q=0（舍去）,q=-2或q=2。故an=（-2）n-1或an=2n-1。

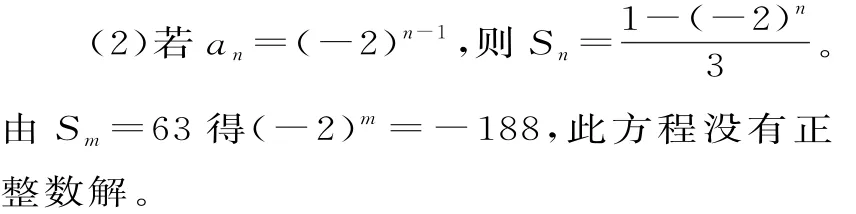
若an=2n-1,则Sn=2n-1。由Sm=63得2m=64,解得m=6。

综上可知,m=6。

反思：等差、等比数列各有五个基本量,两组基本公式,这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化为解关于基本量的方程（组）的问题,有意识地应用等差、等比数列的性质可以简化运算,我们应该注意做到“巧用性质、整体考虑、减少运算量”。

变式2 （2018年全国卷Ⅰ文17）已知数列{an}满足a1=1,nan+1=2（n+1）an,设

（1）求b1,b2,b3;

（2）判断数列{bn}是否为等比数列,并说明理由;

（3）求{an}的通项公式。

聚焦3 利用等比（或等差）数列前n项和与项之间的关系简化求解问题

例3 （2018年全国卷Ⅰ理14）记Sn为数列{an}的前n项和,若Sn=2an+1,则S6=。

解析2：利用一般数列的切入点探究递推关系,根据Sn=2an+1,当n≥2时可得Sn-1=2an-1+1,两式相减整理得an=2an-1（n≥2）。当n=1时,S1=a1=2a1+1,得a1=-1。所以数列{an}是以-1为首项,以2

反思：一般数列的切入点为an=应用中凸显方程组观念及降元意识和分类讨论的方法,但一定要检验n=1时是否满足n≥2时的式子。利用结论“若Sn=kan+b,则{an}为等比数列;若Sn=,则{an}为等差数列”可寻求简化解题的突破口。

变式3 （1）（2018年河南林州一中调研）数列{an}中,已知对任意正整数n,有a1+a2+a3+…+an=2n-1,则+…+=（ ）。

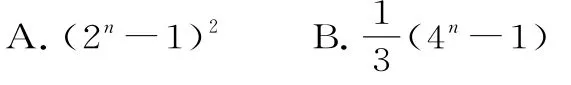
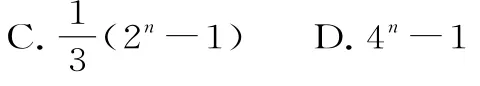
（2）（福建泉州市2017—2018学年高三上学期期末）已知数列{an}的前n项和为Sn,且an＞0,2Sn=an2+an。若不等式2Sn+9≥（-1）nkan对任意的n∈N*恒成立,则k的取值范围是 。

（2）由上面结论和题意知an为等差数列。当n=1时,2a1=+a1,因为an＞0,所以a1=1。当n=2时,2（a1+a2）=+a2,因为a1=1,an＞0,所以a2=2。当n=3时,2（1+2+a3）=+a3,因为an＞0,所以a=3。故a=n。由于2S

3nn+9≥（-1）nkan（n∈N*）,可得:n2+n+9≥（-1）nkn。

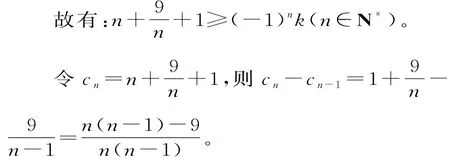
易得,当n≤3时,cn＜cn-1;当n≥4时,cn＞cn-1。

所以,有c1＞c2＞c3=7＜c4=7.25＜c5＜…。

综上可得,k的取值范围是[-7,7.25]。

聚焦4 裂项用公式求特殊数列的和

例4 （2018年天津文18）设{an}是等差数列,其前n项和为Sn（n∈N*）;{bn}是等比数列,公比大于0,其前n项和为Tn（n∈N*）。已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6。

（1）求Sn和Tn;

（2）若Sn+（T1+T2+…+Tn）=an+4bn,求正整数n的值。

解析：可采用基本量法构建方程组求通项进而求和,依据和式的特征裂项直接用公式求和待定参数。

（1）设等比数列{bn}的公比为q,由b1=1,b3=b2+2,可得q2-q-2=0。

因为q＞0,可得q=2,故bn=2n-1。所

设等差数列{an}的公差为d。由b4=a3+a5,可得a1+3d=4。由b5=a4+2a6,可得3a1+13d=16,从而解得a1=1,d=1,故

（2）由（1）知T1+T2+T3+…+Tn=（21+22+23+…+2n）-n=2n+1-n-2。

由Sn+（T1+T2+…+Tn）=an+4bn

整理得n2-3n-4=0,解得n=-1（舍去）,或n=4。所以n的值为4。

反思：对于特殊数列求和,应依据通项选择不同的方法,当通项为多项式时常常裂项用等差或等比数列求和公式求和。

（1）判断数列{bn}是否为等比数列,并求出bn;

（2）求T2n。

聚焦5 裂项相消法求特殊数列的和

例5 （2018年天津理18）设{an}是等比数列,公比大于0,其前n项和为Sn（n∈N*）,{bn}是等差数列。已知a1=1,a3=a2+2,a4=b3+b5,a5=b4+2b6。

（1）求{an}和{bn}的通项公式。

（2）设数列{Sn}的前n项和为Tn（n∈N*）。

（i）求Tn;

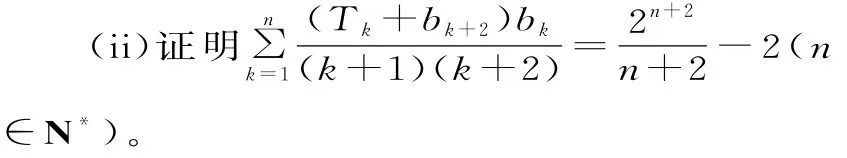
解析：可采用基本量法构建方程组求通项,通项为分式的数列求和,裂项相消法求和证明等式。

（ii）通项为分式,可从通项部分分式裂为两项切入。将bk=k,Tk=2k+1-k-2代入,得:

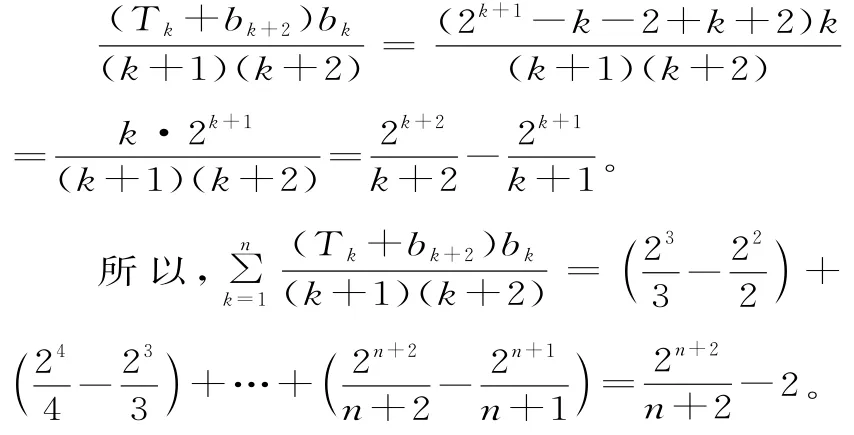
反思：通项为分式的数列求和,常选用对通项部分分式裂为两项,然后重新将数列和的每一项裂为两项,展开后构成n-1个零,进而求出数列的和。常见的裂项方式有:

解析：（1）

由已知Sn=2an-2和Sn-1=2an-1-2（n≥2）可得an=2an-1（n≥2）,即数列an是以2为公比的等比数列,赋值可得到a1=S1=2a1-2,a1=2,故an=2n。

聚焦6 一般数列的切入点应用与错位相减法求和

例6 （2018年浙江20）已知等比数列{an}的公比q＞1,且a3+a4+a5=28,a4+2是a3,a5的等差中项。数列{bn}满足b1=1,数列{（bn+1-bn）an}的前n项和为2n2+n。

（1）求q的值;

（2）求数列{bn}的通项公式。

解析：详细解答请参考本期第38～39页《降低重心 提升素养——谈数列学习与问题求解》一文的例4。

反思：本题是将一般数列的切入点、等差数列求通项的方法与错位相减法有机地进行了交汇。用错位相减法求和应注意:（1）要善于识别题目类型,如等差数列与等比数列对应项的积构成的数列;（2）在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”相减;（3）若公比为参数,应分公比等于1和不等于1两种情况讨论求解。

变式6 （2018年河北唐山二模）数列{an}的前n项和为Sn,Sn=（2n-1）an,且a1=1。

（1）求数列{an}的通项公式;

（2）若bn=nan,求数列{bn}的前n项和Tn。

聚焦7 数列与函数、导数、不等式的交汇

例7 （2018年江苏20）设{an}是首项为a1,公差为d的等差数列,{bn}是首项为b1,公比为q的等比数列。

（1）设a1=0,b1=1,q=2,若|an-bn|≤b1对n=1,2,3,4均成立,求d的取值范围。

（2）若a1=b1＞0,m∈N*,q∈（1,m2],证明:存在d∈R,使得|an-bn|≤b1对n=2,3,…,m+1均成立,并求d的取值范围（用b1,m,q表示）。

解析：可先利用等差和等比数列的定义、通项公式和题设赋值构建不等式组求公差的范围,再依据题设和目标意识解绝对值不等式得到d的区间范围,构造区间端点的函数研究最值进而求解。

（1）由条件知:an=（n-1）d,bn=2n-1。因为|an-bn|≤b1对n=1,2,3,4均成立,即|（n-1）d-2n-1|≤1对n=1,2,3,4均成立,赋值构建不等式组求交集:

（2）存在性证明只需找到一个即可,由条件知:an=b1+（n-1）d,bn=b1qn-1。若存在d,使得|an-bn|≤b1（n=2,3,…,m+1）成立,即|b1+（n-1）d-b1qn-1|≤b1（n=2,3,…,m+1）成立。

设f（x）=2x（1-x）,当x＞0时,f'（x）=（ln2-1-xln 2）2x＜0。

反思：存在性问题的证明只需找到一个即可,对于存在性参数范围问题,常常通过解绝对值不等式求交集求解,复杂的通过解不等式得到参数的上下限,选主元构造上下限的函数,借助定义法（作差或作商）和构造函数导数研究单调性和最值,进而确定存在性参数范围,凸显了数列中的“代数推理、转化与化归、函数导数及不等式”的综合应用以及“探究与创新”解决新颖问题的能力。

变式7 （2018年浙江10）已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln（a1+a2+a3）。若a1＞1,则（ ）。

A.a1＜a3,a2＜a4B.a1＞a3,a2＜a4

C.a1＜a3,a2＞a4D.a1＞a3,a2＞a4

解析：先证不等式x≥ln x+1,再确定公

比的取值范围,进而作出大小判断。

若公比q＞0,则a1+a2+a3+a4＞a1+a2+a3＞ln（a1+a2+a3）,不合题意。

若公比q≤-1,则a1+a2+a3+a4=a1（1+q）（1+q2）≤0,但ln（a1+a2+a3）=ln[a1（1+q+q2）]≥ln a1＞0,即a1+a2+a3+a4≤0＜ln（a1+a2+a3）,不合题意。

因此-1＜q＜0,q2∈（0,1）,故a1＞a1q2=a3,a2＜a2q2=a4＜0,应选B。