基于差分测量的磁梯度张量系统结构寻优
李青竹,李志宁,张英堂,范红波
(陆军工程大学车辆与电气工程系,河北 石家庄 050003)
0 引言
磁异常探测(Magnetic Anomaly Detection,MAD)技术可以对地下或者水下小尺度磁性目标进行定位与识别[1]。相比常规磁矢量分量与总场强度,利用磁梯度张量(Magnetic Gradient Tensor,MGT)进行磁异常探测,能提供目标体更丰富的姿态信息,具有更高空间分辨率,且抗干扰能力强,能够适应较复杂的测量环境[2-3]。磁梯度张量探测具有广阔应用前景,如航空磁测与导航、矿产勘探与土壤黑色金属搜索、探寻未爆弹、排雷、潜艇侦查或水下定位、反演识别等[4-5]。
直接测量磁场梯度本质上难以实现,可将矢量磁传感器阵列组合构建张量系统,利用传感器短距离基线磁矢量差近似估计磁标势二次偏微分,实现张量分量差分测量[6]。目前主要有超导效应和磁通门法两种类型[7-9]:前者采用超导量子干涉仪构建,灵敏度极高但量程范围较小,更适用于小范围微观工况如生物磁测、金属无损探伤等,且成本高,系统安装工艺与测量环境严格;后者利用磁通门传感器阵列测量各正交方向的磁场分量读数空间变化率,其成本更低且安装要求简单,利于批量生产制造。
目前研制的磁梯度张量系统主要有直角四面体型、正四面体型、十字形和三角形等结构,在各自测量条件下均达到了较好的测量效果,但相同条件下不同结构寻优依据不明确,关于磁梯度张量系统结构分析与选型对比研究也鲜有报道。磁传感器的配置结构将直接影响张量的测量可行性及精度,必须优化设计以减小其产生的结构误差[10],确定并搭建最优结构系统是磁梯度张量探测的基础。本文针对此问题,提出了基于差分测量的磁梯度张量系统结构寻优方法。
1 磁梯度张量测量要素
磁梯度张量定义为磁场矢量三分量在各正交方向上的空间变化率[2],共9个元素。若B表示磁场矢量,磁梯度张量矩阵G可表示为:
(1)
式(1),中Bij(i,j=x,y,z)表示磁梯度张量分量,φm表示磁标势,Bx、By、Bz为磁矢量三分量。设环境为无源静磁场,由麦克斯韦方程组知磁场旋度和散度为零,即·B=0,×B=0,为哈密顿算符,则:
(2)
故G对称且无迹,式(1)中9个元素仅5个元素相互独立,有Bxy=Byx、Bxz=Bzx、Byz=Bzy、Bzz=-Bxx-Byy。由式(1)知,磁梯度张量为磁标势φm的二次偏微分和磁场矢量的偏微分,无法直接测量,实际测量中利用不同位置的磁矢量场的差分代替偏微分近似得到磁梯度张量各分量,计算公式为:
(3)
式(3)中,ΔBi为两相邻矢量磁传感器测得的磁场i分量的差,Δdj为两磁传感器j方向上的距离,定义为基线距离。
2 磁梯度张量系统结构分析
2.1 完整磁梯度张量系统及结构误差
磁梯度张量矩阵G的9个元素若均由差分计算得到,则完整的张量系统共需要18个单轴分量输出。在空间建立笛卡尔坐标系,规定x轴正向为东(E),y轴正向为北(N),z轴正向朝上,系统结构如图1所示,由6个矢量磁传感器构成,基线距离为d,整个系统共有18个单分量磁轴。
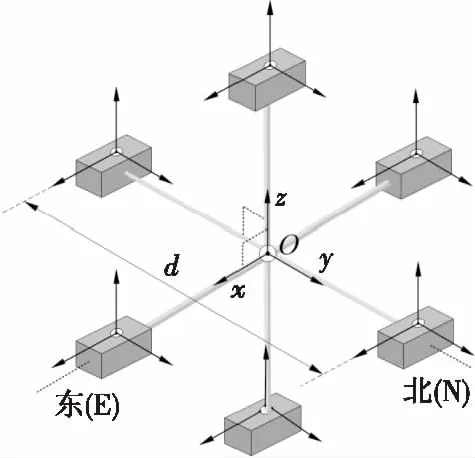
图1 十八单轴磁梯度张量系统结构示意图Fig.1 The configuration of the 18-axle gradient tensor system
因G中九个分量中仅有五个是独立的,因此,可以对张量系统的结构进行优化,使得由传感器配置结构引起的测量误差最小且传感器易于安装和校正。根据式(3),利用差分近似微分时,因忽略了泰勒级数的高阶项,实测磁梯度张量值与理论值存在一定固有偏差,即结构误差,其则系统在结构中心O点的理论二阶张量结构误差矩阵为[9]:
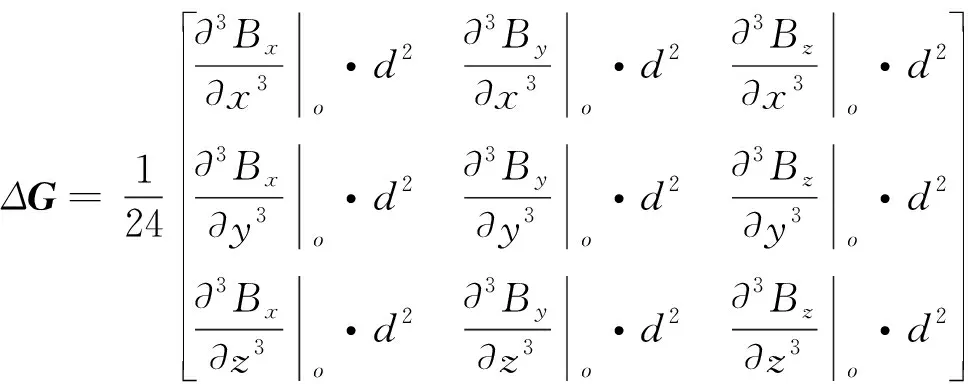
(4)
由式(4)可知,张量系统的结构误差主要由磁矢量的高阶导数和基线距离决定,而随着阶数的增加,高阶导数的量纲迅速衰减,因而结构误差在实际测量中可忽略不计,但在考虑安装和测量方便条件下应尽量选择实际结构误差最小的系统结构。
2.2 五种简化结构及张量测量矩阵
对十八单轴磁梯度张量系统进行简化设计,可变形为平面十字形、等边三角形、正方形、直角四面体型和正四面体型等结构形式,设d为基线距离,传感器
标号为i(i=1,2,3,4),则各配置结构示意图如图2。
设磁传感器分量输出Bpq(p=1,2,3,4;q=x,y,z)表示传感器p在q方向上的磁场分量读数,各结构配置下测得中心O点张量矩阵表达式如下:
1)平面十字形结构
(5)
2)直角四面体型结构
(6)
3)等边三角形结构
(7)
4)正方形结构
(8)
5)正四面体型结构
(9)
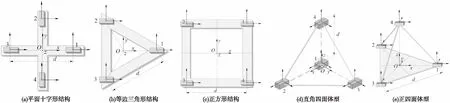
图2 五种简化磁梯度张量系统结构示意图Fig.2 The configuration of 5 kinds of the gradient tensor system
由以上各式知,基于特定结构的特点,十字形、三角形和正方形等平面结构的张量测量矩阵有6个独立分量,而直角四面体和正四面体型机构的张量测量矩阵有9个独立分量。
2.3 系统结构参数与分辨率
传感器之间的基线距离为各种配置类型的张量系统尤为重要的结构参数,在一定程度上直接决定了张量理论测量精度及张量系统探测距离。若希望测得磁性目标的磁磁梯信息,则要求张量系统分辨率高于目标体在该测量点产生的磁梯度张量值。若两传感器以测量点为中心对称排列且基线距离为d,系统分辨率和基线距离与测量点磁场强度间关系可表示为:
(10)
式(10)中,κ表示张量分量测量分辨率,单位为nT/m;e为空间任意方向的单位矢量。分辨率与基线距离成正相关,但并不是说基线距离越小结构误差越小,还与目标磁矩大小、磁传感器精度和定位距离等有关[11],因此需要综合考虑传感器分辨率、探测距离、被探测目标体磁场大小和基线距离等参数进行张量系统搭建。
3 单航线测量试验与结构寻优
由于背景地磁场梯度很小,磁性目标探测时,测量得到的一定范围内磁梯度张量场可认为仅由磁异常场产生。当目标距离测量点大于2.5倍的目标长度时,磁性目标可简化为磁偶极子[12],此时磁性目标可由六个未知量描述,即磁偶极子的位置矢量r=(x,y,z)T和磁矩矢量m=(mx,my,mz)T。磁矩分量可由磁矩模和方向余弦表示,设磁矩模为M=|m|,磁偏角为D,磁倾角为I,则方向余弦为e=cosIcosD、f=cosIsinD、g=sinI,对应的磁矩分量为mx=Me、my=Mf、mx=Mg。磁矩矢量为m的磁偶极子在距离其r处产生的磁场矢量和磁梯度张量的5个独立分量可分别由式(11)、式(12)得到:
(11)
(12)
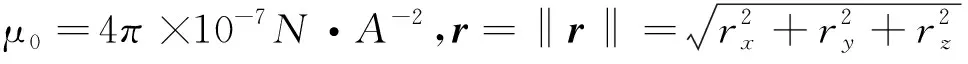
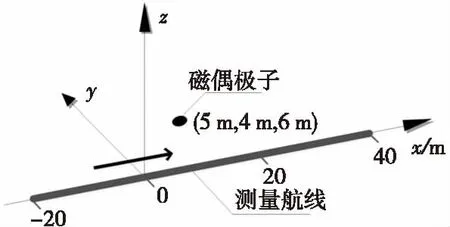
图3 单航线磁偶极子磁梯度场测量试验示意图Fig. 3 Single heading-line survey in magnetic dipole gradient field measurement schematic
由结果可知,推导的各结构张量测量矩阵均能在一定精度范围内实现磁异常体全张量场测量,在相同场源与基线尺寸条件下,平面十字形和正方形结构的测量精度最高,在±500 nT/m的张量分量值测量范围内RMSE控制在0.2 nT/m内,且相比于等边三角形、空间四面体型,结构误差引起的测量偏差小于其10倍以上。此外,平面十字形结构简单便于安装,且方便绕结构中心点Z轴旋转测量较高效地进行传感器系统误差(如非正交性、轴位偏差和灵敏度差等)和阵列间非对准误差的校准作业[14],更具实用性。
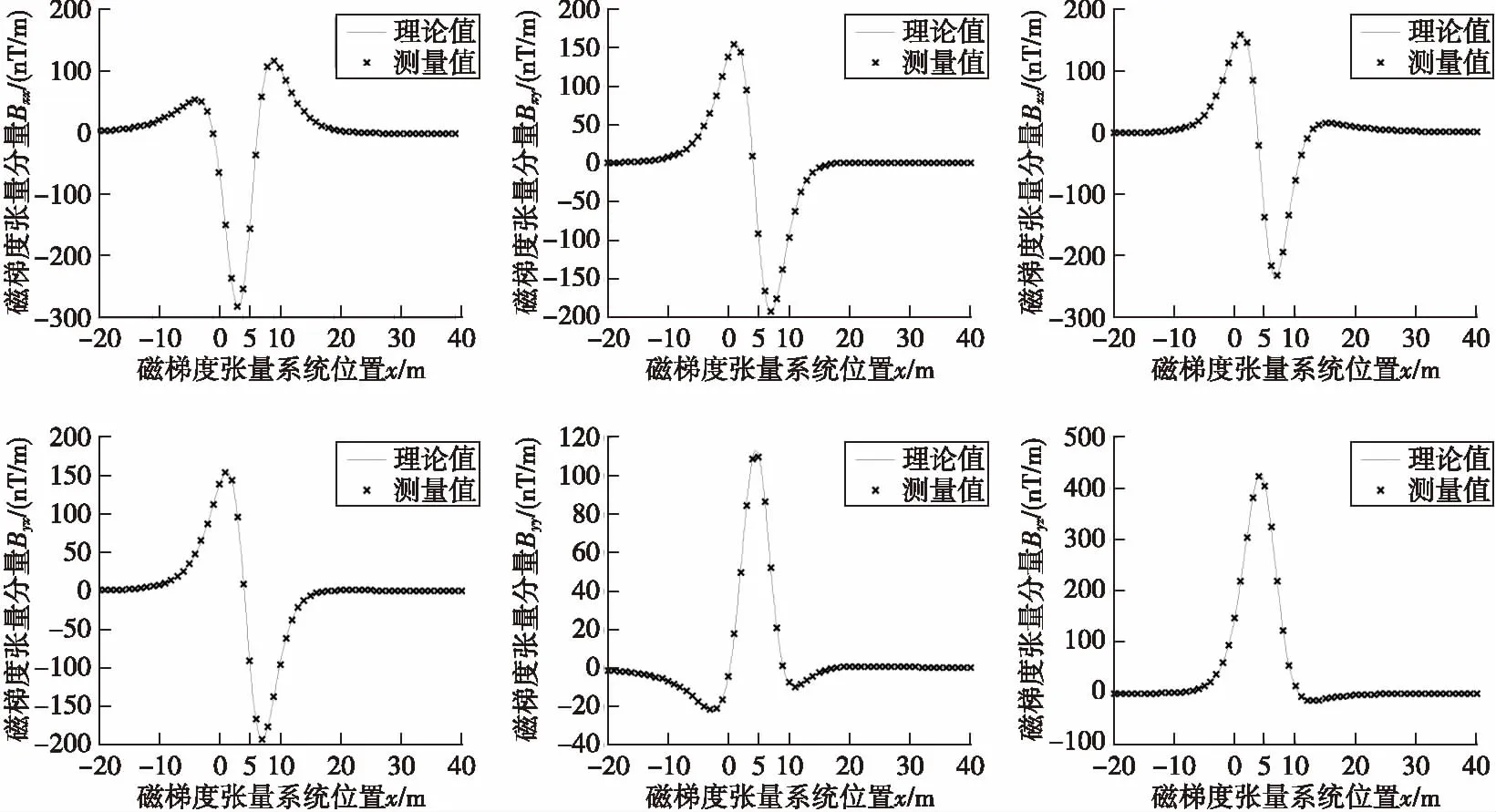
图4 平面十字形磁梯度张量系统的张量分量测量值与理论值对比Fig.4 Comparison of the measured and theoretical values of the tensor components of the cross magnetic gradient tensor system
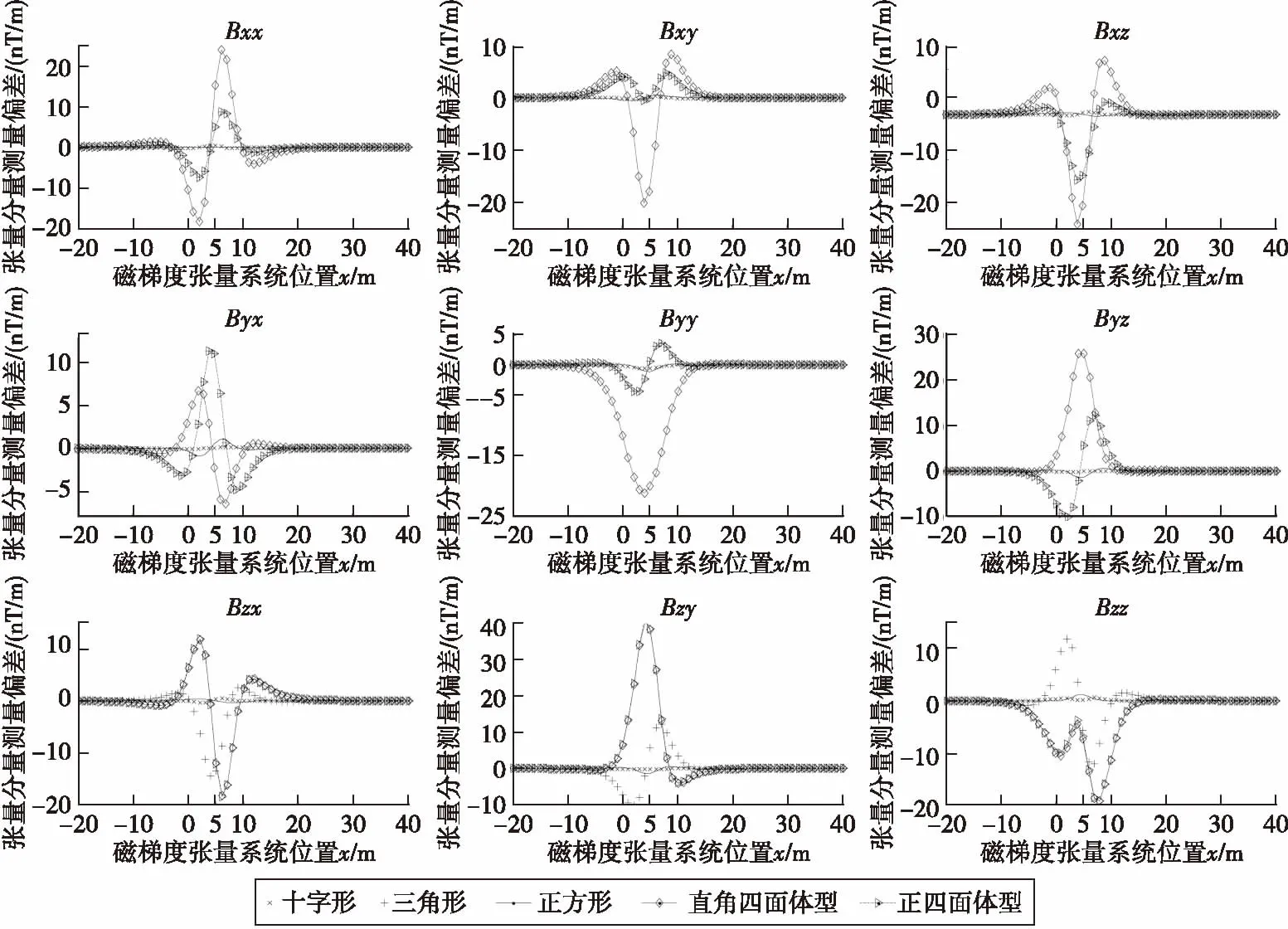
图5 五种结构的张量系统进行单航线测量的张量分量偏差Fig.5 The tensor component deviation of single heading-line survey with tensor systems in five kinds of structures

4 结论
本文提出了基于差分测量的磁梯度张量系统结构寻优方法。根据差分磁梯度张量系统测量原理,该方法分析完整磁梯度张量系统结构配置及结构误差,提出五种简化配置结构的张量系统设计概念并推导了张量测量矩阵及测量分辨率,对五种结构的张量系统进行相同基线尺寸下的单航线磁偶极子磁梯度张量场测量试验从而对系统结构寻优。仿真试验表明,该方法寻优效果明显,对同一测量目标,相同基线尺寸及传感器分辨率条件下,平面十字形和正方形磁梯度张量系统结构误差最小,其理论测量精度最高,且考虑到安装与操作的便捷性及较易于进行传感器误差参数校准,平面十字形结构则更适用于科研与工程实际,而三角形、正四面体和直角四面体型理论测量精度较低,其适用于有特殊结构需求的载体场合,为张量磁测仪器的开发和应用提供参考。

