四元数张量方程A*NX=B 超对称极小范数最小二乘解2
2021-10-13 11:21袁仕芳
井冈山大学学报(自然科学版) 2021年4期
蒋 华,袁仕芳
(五邑大学数学与计算科学学院,广东,江门 529020)
0 引言
本文记RI1×···IN×J1×···×JN为I1×· · ·IN×J1×· · ·×JM实张量集合,CI1×···IN×J1×···×JN为I1×· · ·IN×J1×· · ·×JM复张量集合,QI1×···IN×J1×···×JN为I1×· · ·IN×J1×· · ·×JM四元数张量集合,SSRI1×…×IN为I1×… ×IN实超对称张量集合,SSQI1×…×IN为I1×… ×IN四元数超对称张量集合;对于A∈CI1×…×IN×J1×…×JN,Re(A) ,Im(A) 和A+分别表示张量A的实部、虚部和广义逆。
四元数是William Rowan Hamilton于1843年首次提出的。任意四元数q可以用实数q0,q1,q2,q3唯一表示为

张量A和B的Einstein 积*N定义为

1 几个引理和定义

A和B的行块张量定义为


2 Hilbert 内积空间中的一类线性最小二乘问题

定理2 如果问题II 中的张量方程(15)是不相容的,则问题III 的解集与方程(16)的解集相同。
3 一种张量与向量乘积
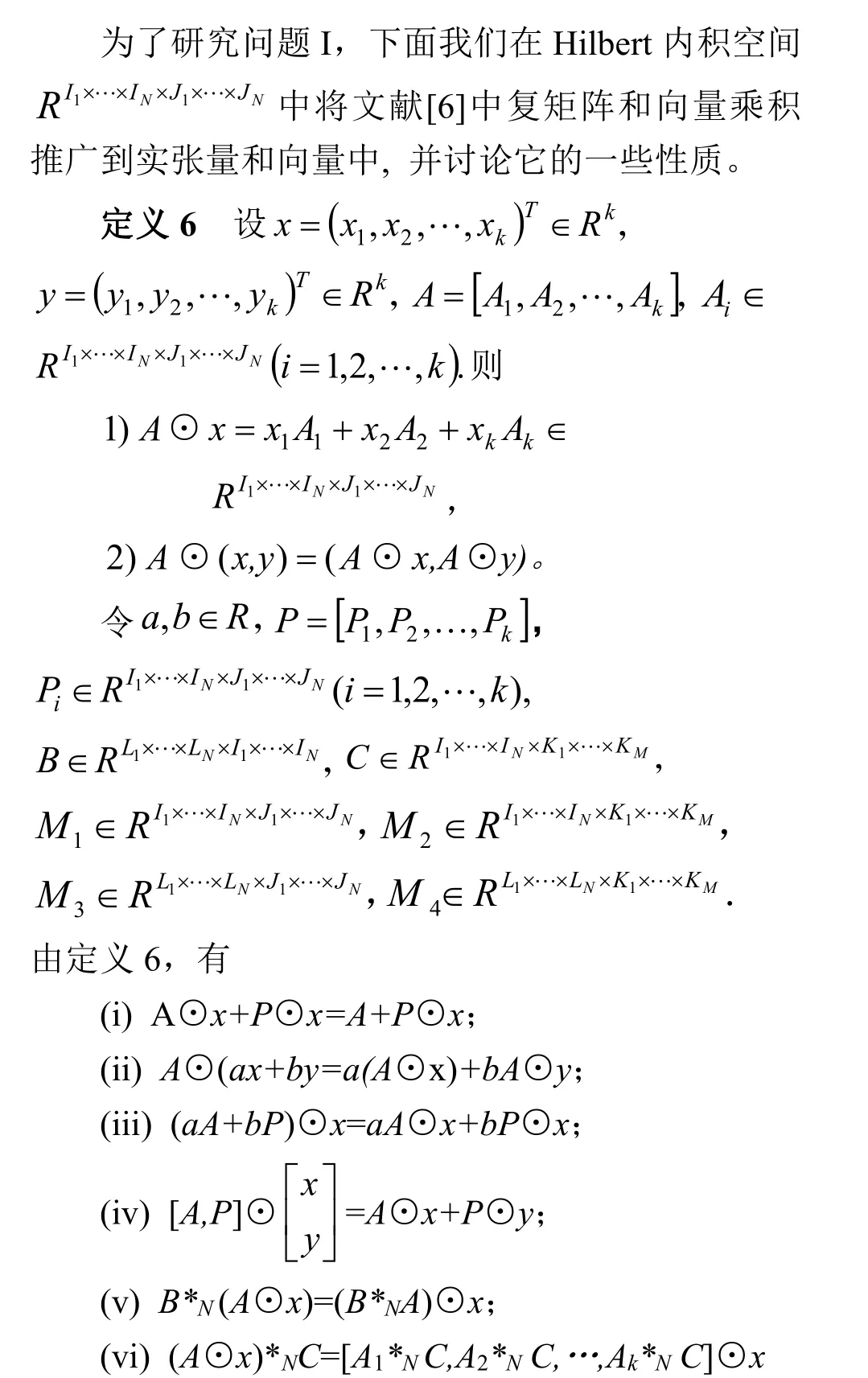
4A *N X = B 在 X∈SS下的结构
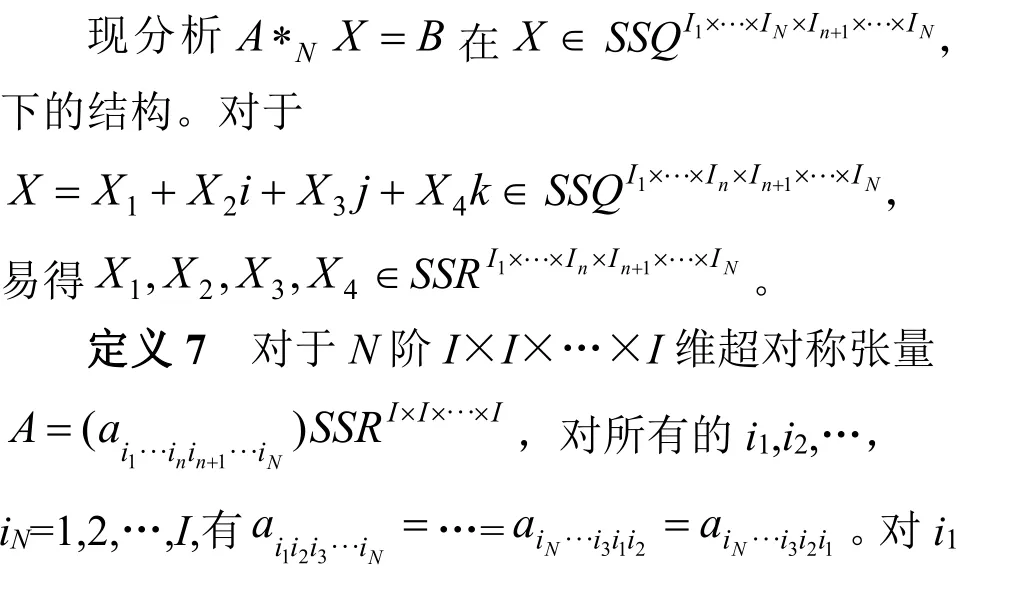


所以


5 问题I 的解
现在求解问题I。利用定理3,可以将四元数张量方程A*NX=B的最小二乘问题转化为实张量方程的最小二乘问题,并用Moore-Penrose广义逆求解。
对于四元数张量

证明 根据定理2 和定理3,问题I 等价于下面相容的矩阵方程


6 数值算法和数值例子
本节利用MATLAB 软件给出求解问题I 的数值算法和数值例子。
算法 1

其中



其中

猜你喜欢
科技信息·学术版(2022年8期)2022-02-25
华南师范大学学报(自然科学版)(2021年3期)2021-07-03
北华大学学报(自然科学版)(2021年1期)2021-03-12
汉语世界(The World of Chinese)(2021年1期)2021-02-22
智能计算机与应用(2020年10期)2020-11-26
中华戏曲(2020年1期)2020-02-12
数学学习与研究(2018年12期)2018-08-17
上海师范大学学报·自然科学版(2018年3期)2018-05-14
上海故事(2016年5期)2016-05-10
海外英语(2013年1期)2013-08-27

