闭黎曼流形上临界度量的研究

肖 飞，俞柏慧

（井冈山大学数理学院，江西，吉安 343009）

0 引言和预备知识

最近几年，刚性定理成为微分几何研究的一个热点。研究者一般考虑带有拼挤条件的Bach平坦黎曼流形[1-2]或者考虑二次曲率泛函的临界点再加pinching条件[3-6],也有学者研究最佳拼挤常数得到有趣的结果[7]。受以上文献启发,本文考虑闭流形上的二次曲率泛函：

拼挤条件用到的Yamabe常数定义如下：

根据Yamabe常数定义，可以得到不等式：

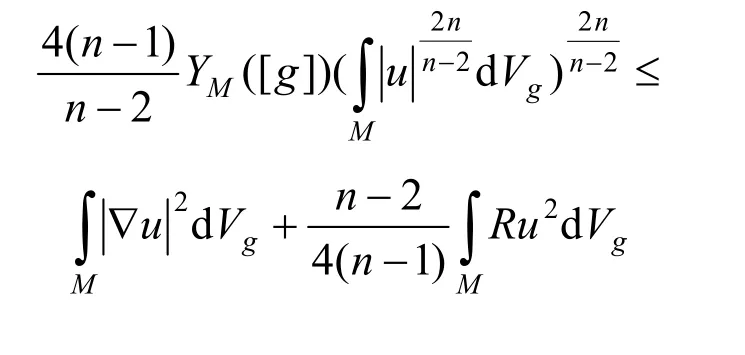
此外，我们知道紧流形上Yamabe常数的符号由其度量共形类的数量曲率的符号所决定。

1 主要结论

2 证明

由推论2 可得推论3。