Hopf流形上全纯向量丛的数字特征

甘 宁

(集美大学理学院,福建厦门361021)

1 Hopf流形及相关概念

Hopf[1]在1948年引进了经典的主Hopf流形，并证明了它是非Kaehler流形从而是非代数流形.Kodaira[2]详细研究了Hopf曲面的性质，Ise[3]计算了Hopf流形上的Dolbeault同调群，Kato[4]研究了Hopf曲面的分类.近段时间研究的一个关注点在Hopf流形上的向量丛，这方面的结果可参考文献[5-9].

复流形上向量丛的Betti数、陈类及Euler示性数等数字特征，是研究向量丛的全纯结构的基本不变量，例如对于2维复流形上全纯向量丛是否存在可滤结构，就与向量丛的陈类密切相关，这方面的结果可参考文献[10].本文计算了高维Hopf流形的数字特征，并且得到了Euler示性数与陈类的关系.

Hopf流形M是一个n维的紧复流形，当n=2时也称作Hopf曲面，其万有覆盖空间双全纯等价于Cn-{0}，它可以表示为商空间的形式M=W/G，其中W=Cn-{0}，G是穿孔复空间Cn-{0}的自同构构成的群，且G是真的不连续以及固定点自由的，G被称为W在M=W/G上的覆盖变换群.当G是无限循环群时，M称为主Hopf流形，否则称为第二类或者非主Hopf流形.

本文中称映射f:(Cn，0)→(Cn，0)，n≥2为一个收缩，它表示f∈Aut(Cn)，f(0)=0,且当n→∞时，fn(B)收敛于0,这里B是Cn中的闭球.若f∈Aut(Cn)，f(0)=0,且具体形式为：f:(z1,z2,…,zn)→(μ1z1,μ2z2,…,μnzn),其中μ1,μ2,…,μn为f′(0)的特征值，且都落在单位圆盘内，则称f为对角收缩.由文献[2,11]可知Hopf流形的基本群G包含一 个收缩f，收缩f生成的无限循环群Z={f}在G中的指数有限，而且{f}位于G的中心，因此{f}是G的正规子群，群G/{f}同构于G中的有限子群H.{f}称作G的无限部分，H称作G的有限部分.因此Hopf流形的基本群G可以写做G={f}·H，即覆盖变换群为无限循环群Z和有限群H的半直积，且对于∀h∈H，f·h=h·f.

2 Hopf流形上的Betti数和陈类

n维紧复流形M的第k个Betti数定义为M的第k个de Rham同调群Hk(M,R)的维数，记为bk(M)，其Betti多项式记为

对于笛卡尔积有公式

P(M×N)=P(M)×P(N).

证明n维的主Hopf流形都微分同胚于S1×S2n-1[12]，这里Sn表示n维的实球面.对于球面Sk，P(Sk)=1+tk.因此有

P(M)=P(S1)×P(S2n-1)=(1+t)(1+t2n-1)=

1+t+t2n-1+t2n.

由此得到M的Betti数b0(M)=b1(M)=b2n-1(M)=b2n(M)=1,b2(M)=b3(M)=…=b2n-2(M)=0.

而M的Euler示性数

0-1+1=0.

由Gauss-Bonnet 公式

可得cn(M)=0.

对于k=2,3,…，2n-1，因为b2(M)=b3(M)=…=b2n-2(M)=0,所以M的de Rham同调群Hk(M，R)=0.而M切丛的陈类cq(M)∈H2q(M，R)，故c1(M)=c2(M)=…=cn-1(M)=0.

□

注1Grauert等[13]给出了Betti多项式求主Hopf流形Betti数的方法，Wehler[14]给出了主Hopf曲面的Betti数和陈类.

定理2n维的非主Hopf流形M的Betti数b2(M)=b3(M)=…=b2n-2(M)=0，M切丛的陈类c1(M)=c2(M)=…=cn-1(M)=0.

证明由前面可知非主Hopf流形M的覆盖变换群G可以写做G={f}·H，即无限循环群{f}和有限群H的半直积，且∀h∈H,f·h=h·f.

这诱导出了上同调群的映射p*

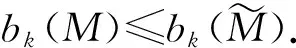
注2对于Kaehler流形，其第2个Betti数b2(M)一定大于0.因此由定理1和2可知，任意的Hopf流形都是非Kaehler流形.

n维的Hopf流形M的万有覆盖空间是W=Cn-{0}.M上的每一个全纯向量丛都可以由覆盖映射π:W→M提升到W上的全纯向量丛，即E的拉回π*(E)，如果π*(E)是全纯平凡的，那么就称E为具有平凡拉回的全纯向量丛.具有平凡拉回的全纯向量丛是比平坦的全纯向量丛更为一般的全纯向量丛.

当全纯向量丛E的秩r=1，即E为全纯线丛时，由文献[7]中Hopf流形上的全纯线丛都是平坦的，因此都是具有平凡拉回的全纯向量丛.下面这个定理为文献[8]中当p=0与E为线丛时定理3的结果.

设E是n维紧复流形M上的全纯向量丛，Hp,q(M,E)为E的Dolbeault同调群，记Hq(M,E)=H0，q(M,E)，称

为向量丛E的Euler示性类.这是向量丛E的重要不变量.

定理3[8]设M是n维的Hopf流形，以及L是M上的全纯线丛，那么有

(i) dimH0(M,L)=dimH1(M,L),

(ii) dimHi(M,L)=0, 2≤i≤n-2,

(iii) dimHn-1(M,L)=dimHn(M,L).

由定理3，可得定理4.

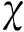
定理5设M是一个n维的非主Hopf流形，则M的第n个陈类cn(M)=0.

证明任取M上的一个全纯线丛L，由Hirzebruch-Riemann-Roch定理和定理4，有

因为L是平坦线丛，故c1(L)=0,由此L的陈特征标Ch(L)=1，从而TM的Todd类Td(TM)有

假设M上的全纯切丛的陈根为d1,d2,…,dn，则利用幂级数展开有

Td(M)在M上积分不为零的项是一个n次的齐次对称多项式，因此可以用d1,d2,…,dn的初等对称多项式来表示.由陈根的定义和定理1,有

d1+d2+…+dn=c1(M)=0,

d1d2+d2d3+…+dn-1dn=c2(M)=0,

⋮

d1d2…dn-1+…+d2…dn-1dn=cn-1(M)=0,

d1d2…dn=cn(M).

因此

这里k是一个常数，由此可得cn(M)=0.

注3由定理1、定理2和定理5,可以得到对于任意的n维Hopf流形，其陈类ck(M)都为零，k=1,2,…,n.

3 Hopf流形上向量丛Euler示性数与陈类的关系

设c0(E),c1(E)…，cr(E)是E的陈类，称

1+c1(E)x+c2(E)x2+…+cr(E)xr

为E的陈多项式，这以多项式可以形式地分解为一次式的乘积

1+c1(E)x+c2(E)x2+…+cr(E)xr=

(1+a1x)(1+a2x)…(1+arx),

则其中a1，a2,…，ar和称为E的陈根.

向量丛E的陈特征标Ch(E)和Todd类Td(E)分别定义为

和

下面这个定理是著名的Hirzebrnch-Riemann-Roch定理[15].

定理6[15]E和TM分别是n维紧复流形M上的全纯向量丛和切丛，则E的Euler示性类

注4需要说明的是，上式中，如果

中的一个同调类不在H2n(M,R)中，则自动视这一同调类在M上的积分为零.

下面的定理需要一个关于n元对称多项式的n次求和公式，设σ1,σ2,…,σn分别是x1,x2,…,xn的初等对称多项式，则

这里的k1,k2,…，kn是非负整数.

定理7设M是一个n维的Hopf流形，E是M上的全纯向量丛，ck(E)表示E的第k个陈类，那么有

证明由注3,知道ck(M)都为零，k=1,2,…,n，故M上切丛的陈根d1=d2=…dn=0,因此

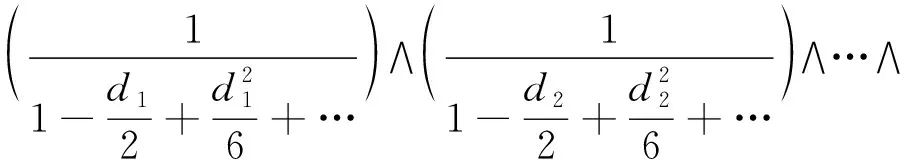
由Hirzebruch-Riemann-Roch 定理，有

E的第k个陈类ck(E)∈H2k(M，R)，由定理1和定理2，对于k=1，2，…,n-1,有b2k=H2k(M,R)=0,因此c1(E)=c2(E)=…=cn-1(E)=0.

设a1，a2,…，ar为E的陈根，则关于a1，a2,…，ar的初等对称多项式

a1+a2+…+an=c1(E)=0,

a1a2+a2a3+…+an-1an=c2(E)=0,

⋮

a1a2…an-1+…+a2…an-1an=cn-1(E)=0.

a1a2…an=cn(E).

因此

c1(E)k1c2(E)k2…cn(E)kn,

这里k1,k2,…,kn是非负整数，但c1(E)=c2(E)=…=cn-1(E)=0,故当k1,k2,…,kn-1=0,kn=1时，上式才有非零项.因此得到

定理8设M是一个n维的Hopf流形，E是M上秩为n的可分全纯向量丛，则

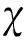
证明因为E是可分全纯向量丛，则存在M上秩分别为r和n-r的全纯向量丛F和G，使得E=F⨁G，因此有

(1+c1(E)+c2(E)+…+cn(E))=(1+c1(F)+

c2(F)+…+cr(F))(1+c1(E)+c2(E)+…+

cn-r(F)).

由定理1和2，当1≤k≤n-1时，b2k=dimH2k(M,R)=0,又陈类ck(E)，ck(F)和ck(G)∈H2k(M,R)，故c1(E)=c2(E)=…=cn-1(E)，c1(F)=c2(F)=…=cr(F)=0和c1(G)=c2(G)=…=cn-r(G)=0.由上面的公式

(1+cn(E))=1,