40阶群和56阶群的同构分类

李德乐,曹慧芹

(1.福建水利电力职业技术学院公共基础部，福建永安366000;2.厦门大学数学科学学院，福建厦门361005)

设G是40阶群，即是23×5阶群.张远达[1]和徐明曜[2]已经分析了40阶群的构造，但是群的构造比较抽象[1,3]，缺乏具体构造方法.本文将继续沿着文献[4]的思路，运用文献[5]的方法，利用Sylow定理，构造G的14种同构类型的群(同构意义下，同构群视为一类群).

对于40阶群，根据Sylow定理，容易看出Sylow 5-子群是正规子群.本文将证明如下定理：

定理1设G是40阶群，P∈Syl2(G),Q∈Syl5(G).G有14种同构类型：(i)P◁G，则G有5种同构类型，见表1中序号1～5所对应的群；(ii)P◁G，则G有9种同构类型，见表1中序号6～14所对应的群.进而应用定理1的方法同理构造了13种56阶群的同构类型.

1 预备知识

在证明定理1之前需要下面一些基本结论：

证明参见文献[5]中定理1的证明.

推论1在引理1的条件和符号下，所有可能的半直积同构类个数恰好等于Ω的Γ-轨道个数.

证明参见文献[5]中推论1的证明.

引理2(Sylow定理)设G是有限群，p是素数且pn‖|G|(即pn||G|但pn+1

|

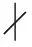
|G|)，则

(i)G必有pn阶子群(称为G的Sylowp-子群).

(ii)G的任意Sylowp-子群皆在G中共轭.

(iii)G的任意Sylowp-子群的个数np是G的因子，且np≡1(modp).

证明具体参考文献[2]证明.

2 定理1的证明

设G是40=23×5阶群，则G必是可解群.设P∈Syl2(G),Q∈Syl5(G),根据Sylow定理，可得Q◁G.下面只考虑P◁G或P◁G两种情况.P同构于8阶群的5种不同类型：

(i) 循环群C8，(ii) 交换群C4×2，即(4,2)-型交换群，(iii) 初等交换群K8，(iv) 二面体群D8，(v) 四元数群Q8，且Q=C5是5阶循环群.

情形1：当P◁G,Q◁G时,则G有5种同构类型：

1)G=〈a,b|a5=b8=1,[a,b]=1〉(循环群)，

表1 40阶群的生成关系表Tab.1 Generating relation table of groups of order 40

2)G=〈a,b,c|a5=b4=c2=1,[a,b]=[b,c]=[c,a]=1〉(交换群)，

3)G=〈a,b,c,d|a5=b2=c2=d2=1,[a,b]=[b,c]=[c,d]=[d,a]=1〉(交换群)，

4)G=〈a,b,c|a5=b4=c2=1,c-1bc=b-1,[a,b]=[a,c]=1〉(C5×D8)，

5)G=〈a,b,c|a5=b4=1,b2=c2,bc=cb-1,[a,b]=[a,c]=1〉(C5×Q8)，

其中a∈Q,b、c、d∈P.

G的结构由P完全决定.令Q=〈a〉=C5，P是8阶群，有5种不同的结构.当P依次取遍8阶群5种不同的结构，相应地可得到G的结构，类型1),2),3)是交换群，类型4),5)是非交换群.

情形2：当P◁G,Q◁G时，则G有9种同构类型，即

6)G=〈a,b|a5=b8=1,b-1ab=a-1〉，

7)G=〈a,b|a5=b8=1,b-1ab=a2〉，

8)G=〈a,b,c|a5=b4=c2=1,bc=cb,b-1ab=a2,ac=ca〉，

9)G=〈a,b,c|a5=b4=c2=1,bc=cb,c-1ac=a-1,ab=ba〉，

10)G=〈ab,bc|a5=b4=c2=1,ac=ca,b-1ab=a-1,bc=cb〉，

11)G=〈a,b,c,d|a5=b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1,b-1ab=a-1,[a,c]=[a,d]=1〉,

12)G=〈ab,c|a5=b4=c2=1,c-1bc=b-1,ab=ba,c-1ac=a-1〉，

13)G=〈a,b,c|a5=b4=c2=1,c-1bc=b-1,b-1ab=a-1,ca=ac〉，

14)G=〈ab2,c,b2|a5=b4=1,b2=c2,c-1bc=b-1,ab=ba,c-1ac=a-1〉.

因为Q◁G，根据N/C定理可知G/CG(Q)≤Aut(Q)≅C4，又Q◁CG(Q)，于是(G/Q)/(CG(Q)/Q)≅P/CG(Q)∩P≤C4，所以P在Q上作用核是2，4或8阶群.

考虑同态φ:P→Aut(Q)，设P在Q上作用核K=CG(Q)∩P，当K是8阶群时，得到G是幂零群，即P◁G,Q◁G，回归到情形1讨论.故只考虑核K是2或4阶群的情形.根据引理1 和推论1，可知作用核是循环群(2阶或4阶)的所有作用都在一个Γ-轨道里，作用核是非循环群(4阶)的所有作用也都在一个Γ-轨道里，其中Γ=Aut(P)×Aut(Q)，因而上述作用最多是3个轨道.设P中元素作用在Q上的非平凡作用就是取平方、取三次方、取逆(即取四次方).下面围绕P同构于8阶群的5种不同类型进行讨论：

(i) 当P=〈b|b8=1〉是循环群时，因为K的阶为2或4，所以K的生成元只有两种不同情况：〈b2〉,〈b4〉.

当K=〈b2〉时，K是4阶循环群，此时b(b∈P且b∉K)诱导Q的自同构是2阶，即ab=b-1ab≠a且ab2=a.设ar=ab(2≤r≤4)，则ab2=(ar)b=ar2=a，即r2≡1(mod5)，解得r=4，因此ab=a4=a-1.P中元素b导出Q的求逆自同构满足ab=b-1ab=a-1，得到上述结构6).

当K=〈b4〉时，K是2阶群，此时b(b∈P且b∉K)诱导Q的自同构是4阶，即ab=b-1ab≠a，且ab4=a.设ar=ab(2≤r≤4)，则ab2=(ar)b=ar2≠a，ab3=ar3≠a，ab4=ar4=a可得r4≡1(mod5)，解得r=2,3.即

当b在a上的作用是取平方时，

ab=a2,(a2)b=a4,(a4)b=a8=a3,(a3)b=

a6=a.

当b在a上的作用是取三次方时，ab=a3,(a3)b=a9=a4,(a4)b=a12=a2,(a2)b=a6=a.

由此可见取三次方与取平方互为逆作用，二者作用效果实质相同，所以只需取平方和三次方两者中的一种情形即可.当K=〈b4〉时，不妨令b取求平方自同构，即b-1ab=a2，从而得到上述结构7).

综上所述，此时G有两种不同类型的群：

根据(i)中计算可知：当K是2阶群时，则元素b(b∈P且b∉K)中诱导Q的自同构是4阶，此时b诱导Q取平方自同构；当K是4阶群时，则b(b∈P且b∉K)中诱导Q的自同构是2阶，此时b诱导Q取逆自同构.

(ii) 当P=〈b,c|b4=c2=1,bc=cb〉是(4，2)-型交换群时，因为K的阶为2或4，所以K的生成元只有3种不同情况：〈b〉，〈c〉,〈b2,c〉.

当K=〈c〉时，K是2阶群，得到元素b(b∈P且b∉K)引起Q自同构为取平方，即b-1ab=a2.记GA(1,5)=〈a,b|a5=b4=1,b-1ab=a2〉为5元域上的一维的一般仿射群，可得：G=GA(1,5)×C2，从而得到上述结构8).

当K=〈b〉时，K是4阶循环群，由元素c(c∈P且c∉K)引起求逆自同构，于是有c-1ac=a-1，即G=D10×C4，得到上述结构9).

当K=〈b2,c〉时，K是4阶初等交换群.根据元素b∈P,b∉K但是b2∈K，可得ab≠a且ab2=a.设ar=ab(2≤r≤4)，则ab2=(ar)b=ar2=a，即r2≡1(mod5)，解得r=4，因此ab=a4=a-1，所以此时P中元素b导出Q的求逆自同构满足ab=b-1ab=a-1.令x=ab，y=bc，G=〈x,y|x20=1,x10=y2,y-1xy=x-1〉=Q40，得到上述结构10).

综上所述，此时G有3种不同类型的群：

根据(ii)中计算，可得当K是4阶初等交换群，此时元素b∈P,b∉K且b2∈K，并且b诱导Q的求逆自同构.

(iii) 当P=〈b,c,d|b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1〉是初等交换群时，由于P中无4阶元，因此同态映射P→Aut(Q)≅C4不可能是满同态，所以K的生成元只有一种情况：〈c,d〉.当K=〈c,d〉时，K是4阶初等交换群，此时元素b(b∈P且b∉K)诱导Q的自同构是2阶，即ab=b-1ab≠a且ab2=a.设ar=ab(2≤r≤4)，则ab2=(ar)b=ar2=a，即r2≡1(mod5)，解得r=4，因此ab=a4=a-1，所以P中元素b导出Q的求逆自同构满足ab=b-1ab=a-1，于是有b-1ab=a-1，即

G=〈a,b,c,d|a5=b2=c2=d2=1,[b,c]=

[c,d]=[d,b]=1,b-1ab=a-1,[a,c]=

[a,d]=1〉=D10×K4，

从而得到上述结构11).

(iv) 当P=〈b,c|b4=c2=1,c-1bc=b-1〉是二面体群结构时，由于同态映射P→Aut(Q)≅C4不可能是满同态，否则C4≅P/Z(P)，得到P是交换群，与P是二面体群相矛盾，故K的生成元可有两种不同情况：〈b〉,〈b2,c〉.

当K=〈b〉时，K是4阶循环群，由元素c(c∈P且c∉K)引起求逆自同构，于是有c-1ac=a-1，令x=ab，y=c，则G=〈x,y|x20=y2=1,y-1xy=x-1〉=D40，得到上述结构12).

当K=〈b2,c〉时，K是4阶初等交换群，由b引起求逆自同构，于是有b-1ab=a-1，得到上述结构13).

综上所述，此时G有两种不同类型的群：

(v) 当P=〈b,c|b4=1,b2=c2,c-1bc=b-1〉是广义四元数群时，P中有唯一的2阶元，所以核K不能是4阶初等交换群.由于同态映射P→Aut(Q)≅C4不可能是满同态，否则C4≅P/Z(P)，得到P是交换群，与P是四元数群相矛盾，故K的生成元只有一种情况：〈b〉.当K=〈b〉时，K必是4阶循环群，由c(c∈P且c∉K)引起Q求逆自同构，于是有c-1ac=a-1.令x=ab2，y=c，z=b2，则G=〈x,y,z|x10=y2=z2=1,x5=y2,y-1xy=x-1,zx=xz,zy=yz〉=Q20×C2，得到G=〈ab2,c,b2|a5=b4=1,b2=c2,c-1bc=b-1,ab=ba,c-1ac=a-1〉=Q20×C2，

即上述结构14).定理1证毕.

3 应 用

利用上述的理论，很容易构造56群的13种同构类型.由Sylow定理可知：56阶群不可能是单群.设G是56阶群，即是23×7阶群，也是可解群，并设P∈Syl2(G),Q∈Syl7(G),要分成(i)P◁G,Q◁G；(ii)P◁G,Q◁G；(iii)P◁G,Q◁G3种情况加以讨论.设Q=〈a〉=C7.

情形1：当P◁G,Q◁G时，则G有5种同构类型：

15)G=〈a,b|a7=b8=1,[a,b]=1〉(循环群)，

16)G=〈a,b,c|a7=b4=c2=1,[a,b]=[b,c]=[c,a]=1〉(交换群)，

17)G=〈a,b,c,d|a7=b2=c2=d2=1,[a,b]=[b,c]=[c,d]=[d,a]=1〉(交换群)，

18)G=〈a,b,c|a7=b4=c2=1,bc=cb-1,[a,b]=[a,c]=1〉(C7×D8)，

19)G=〈a,b,c|a7=b4=1,b2=c2,bc=cb-1,[a,b]=[a,c]=1〉(C7×Q8)，

因为P◁G,Q◁G，G的结构由P完全决定.P是8阶群，有5种不同的结构.当P依次取遍8阶群5种不同的结构，相应地可得到G的结构，类型15)，16)，17)是交换群，类型18)，19)是非交换群.

情形2：当P◁G,Q◁G时，则G有7种不同构类型：

21)G=〈ab,bc|a7=b4=c2=1,bc=cb,ba=ab,c-1ac=a-1〉=Q56，

22)G=〈a,b,c|a7=b4=c2=1,bc=cb,b-1ab=a-1,ca=ac〉=D28×C2，

23)G=〈a,b,c,d|a7=b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1,b-1ab=a-1,[a,c]=[a,d]=1〉=D14×K4，

24)G=〈ab,c|a7=b4=c2=1,c-1bc=b-1,ba=ab,c-1ac=a-1〉=D56，

25)G=〈a,b,c|a7=b4=c2=1,c-1bc=b-1,b-1ab=a,ca=ac〉，

26)G=〈ab2,c,b2|a7=b4=c2=1,c-1bc=b-1,ab=ba,c-1ac=a〉.

因为Q◁G，根据N/C定理可知：G/CG(Q)≤Aut(Q)=Aut(C7)≅C6，考虑到P作用Q上的是非平凡作用，因为Q◁CG(Q)，所以P在Q上作用核只能是4阶群.设P在Q上作用核K=CG(Q)∩P，根据引理1和推论1，可知要构造G的关系就是确定作用核K和P中诱导Q的求逆自同构的元素.

(b) 当P=〈b，c|b4=c2=1,bc=cb〉是(4，2)型交换群时，因为K的阶为4，所以K的生成元只有两种不同情况：〈b〉，〈b2,c〉.

当K=〈b〉时，K是4阶循环群.根据c(c∈P且c∉K)诱导Q的自同构是2阶，即c(c∈P且c∉K)引起求逆自同构，于是有c-1ac=a-1.令x=ab，y=bc，则G=〈x,y|x28=1,x14=y2,y-1xy=x-1〉=Q56，得到上述结构21).

当K=〈b2,c〉时，K是4阶初等交换群.因为b∈P,b∉K且b2∈K，所以b引起求逆自同构，可取b-1ab=a-1，即G=D28×C2，得到上述结构22).

综上所述，此时G有两种不同类型的群：

(c) 当P=〈b,c,d|b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1〉是初等交换群时，因为K是4阶初等交换群，则K=〈c,d〉，此时元素b(b∈P且b∉K)诱导Q的自同构是2阶，即ab=b-1ab≠a且ab2=a.设ar=ab(2≤r≤6)，则ab2=(ar)b=ar2=a，即r2≡1(mod7)，解得r=6，即ab=a6=a-1.P中元素b导出Q的求逆自同构，即ab=b-1ab=a-1，即G=〈a,b,c,d|a7=b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1,b-1ab=a-1,[a,c]=[a,d]=1〉=D14×K4，

得到上述结构23).

(d) 当P=〈b，c|b4=c2=1,c-1bc=b-1〉是二面体群结构时，K的生成元可有两种不同情况：〈b〉,〈b2,c〉.

当K=〈b〉时，K是4阶循环群.元素c(c∈P且c∉K)引起Q求逆自同构，于是有c-1ac=a-1.令x=ab，y=c，则G=〈x,y|x28=y2=1,y-1xy=x-1〉=D56，得到上述结构24).

当K=〈b2,c〉时，K是4阶初等交换群.因为b∈P，b∉K且b2∈K，所以由b引起求逆自同构，于是有b-1ab=a-1，得到上述结构25).

综上所述，此时G有两种不同类型的群：

(e) 当P=〈b,c|b4=1,b2=c2,c-1bc=b-1〉是四元数群时，P中有唯一的2阶元，因此K不能是4阶初等交换群，此时K的生成元只有一种情况：〈b〉.即K=〈b〉必是4阶循环群，由c(c∈P且c∉K)引起Q求逆自同构，于是有c-1ac=a-1.令x=ab2，y=c，z=b2，则G=〈x,y,z|x14=y2=z2=1,x7=y2,y-1xy=x-1,zx=xz,zy=yz〉=Q28×C2，得到G=〈ab2,c,b2|a7=b4=1,b2=c2,c-1bc=b-1,ab=ba,c-1ac=a-1〉=Q28×C2，即上述结构26).

情形3：当P◁G，Q◁G时，则G有一种不同构类型：

27)G=〈a,b,c,d|a7=b2=c2=d2=1,[b,c]=[c,d]=[d,b]=1,a-1ba=d-1,a-1ca=bd-1,a-1da=c〉.