基于变结构控制的引信滚转角控制方法

雷泷杰，陈瑞华，施坤林

(1. 西安机电信息技术研究所,陕西 西安 710065;2.北方智能微机电集团有限公司,北京 101149)

0 引言

采用二维弹道修正引信使得传统弹药灵巧化的概念近几年已深入人心，通过将传统引信替换成具有弹道修正功能的二维弹道修正引信的方式，使得无控弹药同时具备射程方向和横偏方向上修正能力，从而实现对面目标的打击。目前多采取鸭舵方式实现弹丸姿态的改变，进而产生所需方向修正力[1]。目前国外以美国PGK(Precision Guidance Kit)方案和英国的“银弹”整体减旋方案为代表，已经应用到了作战使用中。国内研究的较多的是类似PGK方案，对于整体减旋方案的研究较少，均处于初步研究阶段[2]。对于这两种方案而言，滚转角控制都是一项关键技术。

国内对于二维弹道修正引信滚转角控制的研究内容相对较少，文献[3]中提出了二维弹道修正引信滚转角双闭环控制方法，但未给出具体的滚转角控制器设计思路。文献[4]中提出了一种针对PGK方案设计的滚转角模糊控制方法，该方法控制精度较为理想，但工程实现性较差。文献[5]中针对整体减旋方案提出了基于线性二次型调节器算法的滚转角控制方法，该方法对于系统建模准确度要求较高，该方法工程应用性较差。本文针对现有二维弹道修正引信滚转角控制方法存在模型依赖性强、工程可实现性差问题，提出了基于变结构控制的引信滚转角控制方法。

1 滚转角运动数学模型及变结构控制理论

1.1 二维弹道修正引信滚转角运动的状态空间描述

无论是PGK方案还是整体减旋方案，对于二维弹道修正引信而言，在飞行过程中主要受到作用在导转翼面的气动导转力矩以及升力翼面产生的干扰导转力矩，同时受到来自弹丸的耦合力矩。对于PGK方案，耦合力矩为主动控制力矩；对于整体减旋方案，耦合力矩主要包括弹丸与引信之间的相对转动所产生的摩擦力矩以及气动干扰力矩，均为被动干扰力矩。同时引信受到由转动引起的滚转阻尼力矩[6]。采用鸭舵修正技术的二维弹道修正引信的外形及安装示意图如图1所示。

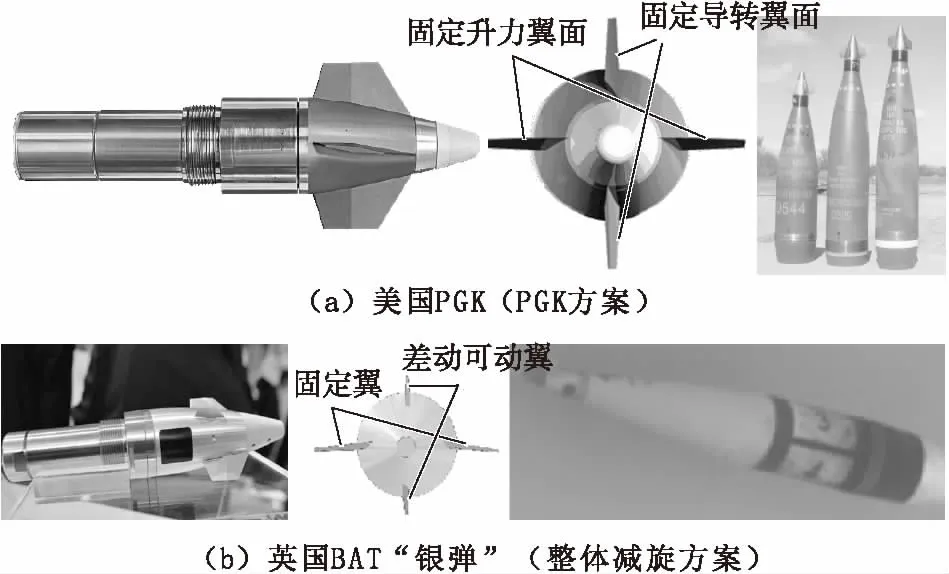
图1 二维弹道修正引信PGK方案及整体减旋方案Fig.1 PGK program and whole despining program of 2-D trajectory correction fuze

引信绕其纵轴转动的动力学以及运动学非线性微分方程组如式(1)所示[5]。

(1)

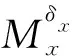
耦合力矩对于PGK方案而言主要指主动电磁控制力矩以及翼面与弹丸之间的轴承摩擦力矩，对于整体减旋方案而言主要指弹丸与引信之间相对转动所产生的摩擦力矩，干扰力矩主要包括升力翼面产生的干扰导转力矩以及弹丸与引信之间的气动干扰力矩。

由于弹丸在飞行过程中攻角及侧滑角变化较小，则利用小扰动假设理论可以简化得到二维弹道修正引信滚转角运动的状态空间描述[7]。

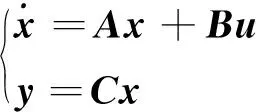
(2)

1.2 变结构控制理论

变结构控制(VSC, Variable Structure Control)最初在20世纪60年代由苏联学者提出并研究，短短几十年里，变结构控制理论发展迅速，逐步形成控制理论的一个分支。变结构控制系统已经被用来解决各种复杂的控制问题。

对于形如式(2)的系统，选取式(3)所示的切换平面

s=f(x1,x2,…,xn)=0

(3)

式(3)中，(x1,x2,…,xn)T为系统状态向量。

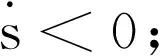
在切换平面s=0附近的n维δ临域，系统的状态轨迹均指向它(见图 2)，这意味着系统状态点一旦进入该切换平面，只能沿其运动而很难离开，若要离开这一区域只能穿越切换平面s=0，这一区域便是系统的一个滑动模态域。

图2 变结构控制原理示意图Fig.2 Sketch map of variable structure control’s principle

变结构控制与传统控制方法最大区别在于，变结构控制是通过选取合适的趋近律，进而调节反馈控制器的结构，使得系统的状态在合适趋近律下能够到达某个具有特定函数值的切换平面时，同时要求该切换平面内存在滑动模态域，当系统状态向量进入滑动模态域后便沿其运动，在滑动模态域内系统显示出很强的对不确定因素的鲁棒性，使得系统由一种结构变为另一种结构的控制方法[8]。

2 引信滚转角的变结构控制

二维弹道修正引信滚转角控制的目的是使得引信滚转角γfuze跟踪滚转角控制指令γfuzeC，即要求引信滚转角与滚转角控制指令误差为零，由上述变结构控制理论可知，变结构控制的最终目的是使系统状态为零，应用变结构控制可以满足引信滚转角控制问题，引信滚转角的变结构控制关键在于选取切换平面以及合适的趋近律，使得引信滚转角能够实现对滚转角指令的跟踪，最终便可以保证修正弹的打击精度。

首先，应用变结构控制理论，定义滚转角控制系统误差变量e。

e=γfuzeC-γfuze

(4)

其次，定义式(5)所示的滑动模态s，并选取切换平面s=0。

(5)

式(5)中，kγ一般为正数，用来保证滑动模态的收敛，即切换平面附近存在滑动模态域。

(6)

最后，采用式(6)所示的趋近律。

(7)

式(7)中，k1和k2均大于0。

结合式(5)和式(6)可得PGK方案以及整体减旋方案二维弹道修正引信滚转角控制律。为了消除变结构控制器中由于符号函数换向所带来的抖振现象，采用线性饱和函数代替符号函数。则PGK方案以及整体减旋方案二维弹道修正引信滚转角控制律分别如式(8)和式(9)所示。

(8)

(9)

式(9)中，δx表示整体减旋方案中的导转翼面偏角或等效偏角，Mxctrl表示PGK方案中的电磁控制力矩,Mf表示轴承摩擦力矩。

在系统处于第一阶段的能达阶段(s≠0)时，定义李雅普诺夫函数

(10)

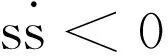
在系统进入第二阶段的滑动阶段(s=0)时，定义李雅普诺夫函数

(10)

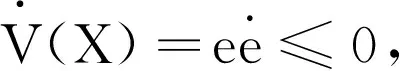
3 仿真验证

在不引入测量误差的情况下对高旋榴弹平台1.2Ma下的整体减旋方案和PGK方案的二维弹道修正引信滚转角控制系统进行了仿真，引信滚转角初始状态为0°，滚转角控制指令为180°，仿真步长0.001 s。仿真结果如图 3所示。

图3 二维弹道修正引信滚转角控制仿真曲线Fig.3 Simulation diagram of roll angle control system on 2-D trajectory correctionfuze

表1给出了图3中控制仿真结果的各项时域指标分析结果。从中可以看出，无论对于采用整体减旋方案的二维弹道修正引信还是采用PGK方案的二维弹道修正引信而言，滚转角控制的各项时域指标分析结果均表明变结构控制精度优于传统PID(Proportion Integral Differential,比例积分微分)控制精度。

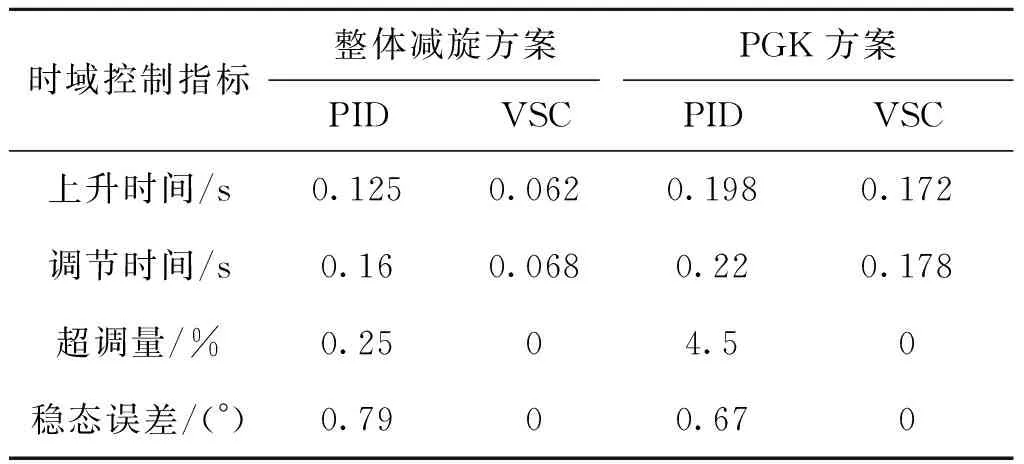
表1 二维弹道修正引信滚转角控制 仿真时域指标分析结果Tab.1 The analytical time-domain indices ofroll angle control system on 2-D trajectory correctionfuze

二维弹道修正引信滚转角控制系统会存在各种误差和干扰。主要包括滚转角及滚转角速度测量误差、摩擦力矩散布误差以及由于气象环境变化或弹丸气流角的变化而引起的气动干扰误差，表2给出了弹丸在实际飞行过程中主要误差源及参考值。引入表2中给出的各项误差和干扰，分别对采用PID控制器以及采用变结构控制器进行了仿真，仿真结果如图4所示。

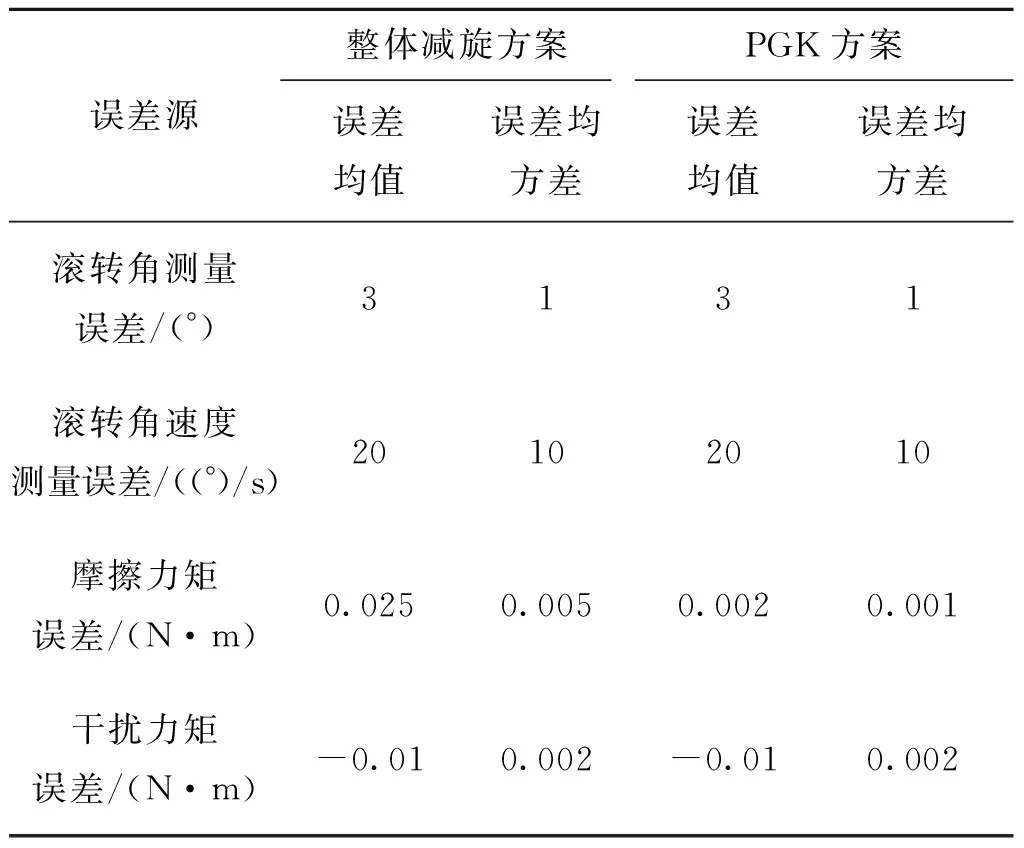
表2 二维弹道修正引信滚转角控制仿真误差源Tab.2 Simulation error resources of roll angle control system on 2-Dtrajectory correction fuze

整体减旋方案采用PID控制器的滚转角控制精度为误差均值-2.306 9°，误差均方差0.820 3°；采用变结构控制器的滚转角控制精度为误差均值0.382 4°，误差均方差0.4816°。PGK方案采用PID控制器的滚转角控制精度为误差均值-3.250 2°，误差均方差1.533 7°；采用变结构控制器的滚转角控制精度为误差均值-0.138 0°，误差均方差0.237 1°。从上述仿真结果可以看出，无论是整体减旋方案还是PGK方案，采用变结构控制器的滚转角控制精度要比采用传统PID控制器的滚转角控制精度更高，采用变结构控制器系统对噪声的抗干扰能力更强,亦即鲁棒性更强。

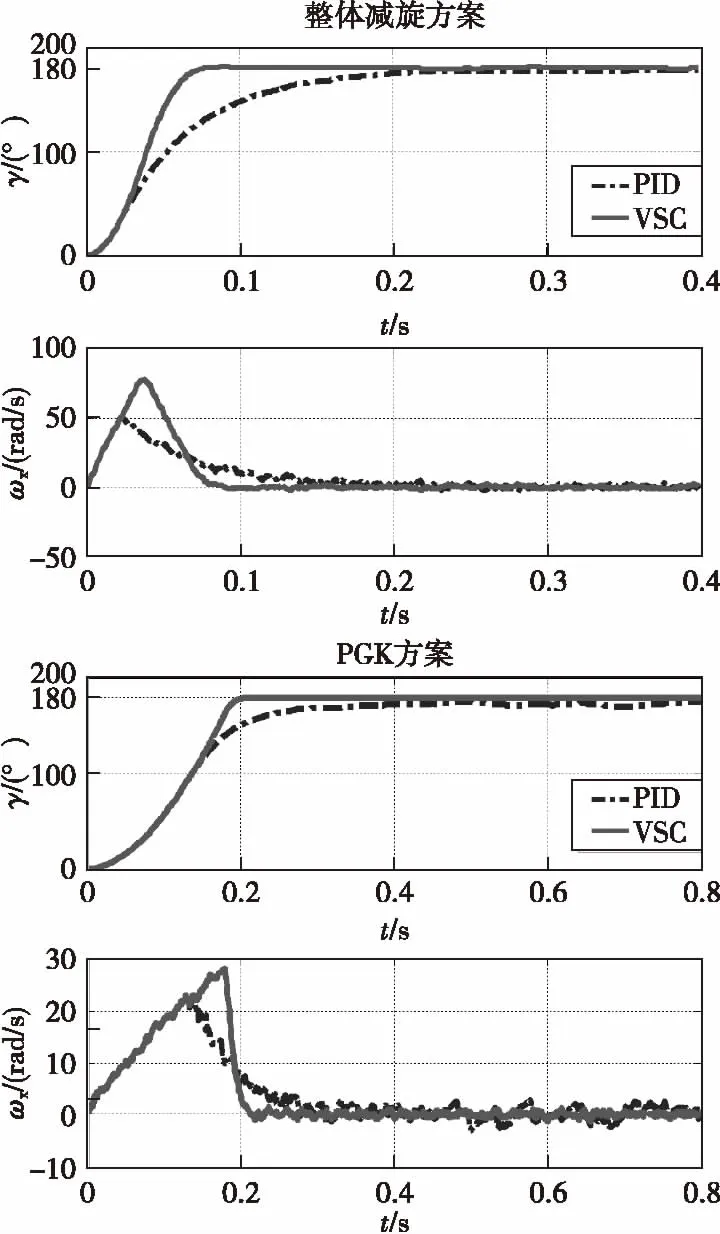
图4 引入误差和干扰时二维弹道修正 引信滚转角控制系统仿真曲线Fig.4 Diagram of roll angle control system on 2-D course correctionfuze with errors and interference

4 结论

本文提出了基于变结构控制的引信滚转角控制方法。该方法建立了描述二维弹道修正引信滚转角运动的状态空间描述，通过选取了切换平面以及合适的趋近律，设计了二维弹道修正引信滚转角的变结构控制器，同时保证了控制系统的稳定性，并显示出较强的抗干扰能力。理论分析与仿真验证表明，基于变结构控制的引信滚转角控制方法与传统的双闭环PID控制相比，控制系统对干扰具有强鲁棒性，且控制精度更高。