基于阻塞矩阵预处理的抗主瓣干扰算法
胡海涛,张剑云,李小波,周青松
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
近年来抗雷达主瓣干扰成为研究的热点,针对雷达的主瓣干扰已经提出了多种算法,王建明提出了利用特征矩阵近似联合对角化的盲源分离算法抗主瓣干扰技术[1],但当信噪比较低的情况下效果下降显著,之后周青松等人对此做了改进,首先对接收到的信号进行盲源分离,然后利用分数阶傅里叶变化(FRFT)对分离的信号进行处理[2],但是这种算法破坏了信号的本身特性,对后期信号的参数估计带来了困难。董玮等人提出了基于约束独立分量分析的雷达抗主瓣干扰算法[3],该算法对非相干干扰信号可以取得较好的分离效果,但是对于相干干扰不能有效地分离目标信号和干扰信号。戴幻尧利用天线的极化特性,研究了利用信号的极化特性滤除主瓣干扰的算法[4],但是这种算法的抗干扰性能有限。胡航研究了单脉冲四通道主瓣干扰抑制算法[5],这种算法相对于三通道而言多构造出一个双差波束,将主瓣干扰抑制掉。但是这种算法相对于传统的三通道单脉冲测角而言,增加了系统的复杂度,且这种算法只能抑制掉一个主瓣干扰。S.J.Yu提出了用阻塞矩阵预处理的算法[6],但是当存在主瓣干扰时可能会导致主瓣波束失真等问题。由于该算法思路比较清晰,而且取得了很好的效果,得到了广泛的关注,Carlson B D.说明了对自适应线性约束最小功率波束形成算法最优权矢量可以表示为波束形成的对角加载形式[7],但无法对加载电平进行精确地求解,只能用数值估计的方法得到近似解。Yang J提出了一种基于对角加载和线性约束相结合的方法[8]来解决主瓣波束失真的问题,加载电平选取为数据协方差矩阵除去较大特征值后的平均值,但是这种方法对特征值平均值的计算也不易选取。本文针对这一问题,对主瓣方向发生的原因进行了详细的分析,提出了改进的基于阻塞矩阵预处理的抗主瓣干扰算法。
1 信号模型
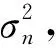
X=[x1,…,xM]=AS(t)+n(t)
(1)
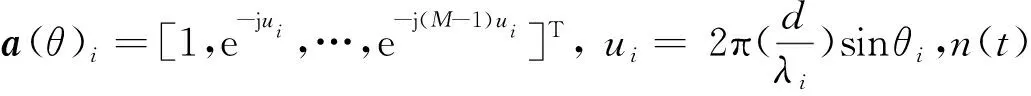
当采用自适应波束形成算法抗干扰时,对接收到的样本进行加权,生成的权矢量能自适应地在样本信号方向形成零陷,从而能抑制干扰。假设样本中只有干扰和噪声信号,则可表示为:
Xn+i(k)=An+iSn+i(k)+n(k)=
(2)
式(2)中,k为快拍数,k=1,…,K,Xn+i为N×1维的干扰噪声的数据,An+i表示干扰信号的导向矢量组成的矩阵,Sn+i表示干扰信号的P×1维矢量。为了方便分析,在后面算法的推导中均用X(k)表示阵元接收到的干扰和噪声Xn+i(k)。
2 基于阻塞矩阵预处理的抗主瓣干扰算法
2.1 阻塞矩阵预处理算法波形失真分析
假设有干扰信号从天线的主瓣进入,为了抑制干扰,首先利用空间谱估计理论估计出干扰信号的方位角,由于主瓣的干扰信号是从主瓣进入的,所以干扰信号的能量一般大于信号和干扰的噪声,利用ESPRIT算法或者MUSIC算法可以精确地估计出干扰信号从主瓣进入的方向:
(3)
式(3)中,Un为阵列接收到的干扰和噪声的协方差矩阵对应的特征向量,a(θ)为导向矢量。与MUSIC算法谱峰相对应的是干扰信号的DOA,由于利用阻塞矩阵对消主瓣上的干扰只需要知道主瓣的干扰方向,所以在搜索从主瓣方向进入干扰信号的DOA时,只需在主瓣宽度方向上搜索,这样可以减少计算量。
当估计出主瓣干扰的DOA时,对样本信号进行干扰对消预处理,假设预处理后的信号为Y,则Y=BX,其中B为:
(4)
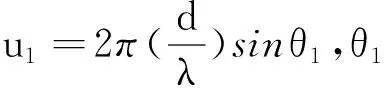
干扰对消前,第k个天线接收到的信号可以表示为
(5)
经过处理后的Y显然为N-1维的向量,干扰对消后第k个天线接收到的信号可以表示为:
(6)
对于经过阻塞矩阵预处理之后的天线方向图会发生偏移,分析如下:
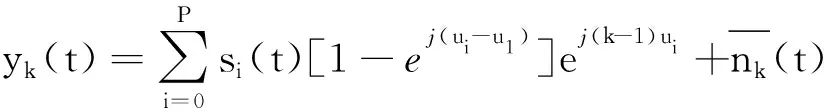
Y1=A1S1+n1
(7)
可以看出经过阻塞矩阵对消后没有改变信号的波达方向,但是经过预处理后损失了一个天线的自由度,导致期望信号的导向矢量和经过预处理后剩余干扰相对于未经预处理的丢失了一维,而导向矢量的另一维却没有变。假设用N-1阵列接收只包含目标信号和剩余的干扰信号,则
Y0=A0S0+n0
(8)
显然A1=A0,S1=S0Λ,其中Λ=diag{1-ej(u0-u1),1-ej(u2-u1)…,1-ej(uP-u1)}。
所以
RY=E[YYH]=E[Y1YH]=
A1RS1A1H+E[n1n1H]=
A1RS1A1H+σn2BBH
(9)
类似的有
RY0=E[Y0Y0H]=A0RS0A0H+E[n0n0H]=A0RS0A0H+σn2I
(10)
式(9)中,RS1=E[S0S0H]。
比较RY和RY0,我们可以看出两者的协方差矩阵并不相同,而经过预处理后的数据RY在自适应波束形成时使用了理想的导向矢量,所以处理后的主瓣方向会有主瓣发生偏移、变形和副瓣电平增高等问题。
为了克服这一问题,文献[8]提出了一种基于对角加载的算法来解决主瓣方向偏移的问题,通过该算法有效地解决了阻塞矩阵预处理之后波束形成主波束发生偏移的问题,但是该算法对于对角加载的电平的选取,是靠经验选取的,如果加载电平过小将导致加载量不够,主瓣偏移不能得到很好地解决,而如果加载电平选取的过大,尽管主瓣能很好地对准目标方向,但将导致副瓣的零陷发生偏移,与副瓣的干扰方位不同。
2.2 基于二次不等式约束的LCMV波束形成算法
对于线性约束最小方差(LCMV)波束形成算法的加权矢量二次约束可以有效地改善波束指向与信号的不适配问题,最佳加权矢量可以表示为LCMV算法的对角加载形式为:
w=(Rx+λI)-1C[CH(Rx+λI)-1C]-1f
(11)
通过仿真验证了该算法能有效解决波束指向发生偏移的问题,但是对于加载量λ的选取没有理论的分析,经验因素影响较大。
通过上述分析,由于利用阻塞矩阵对信号预处理后,得到的导向矢量与真实的导向矢量有一定的误差,为了满足在期望信号方向无失真的接收,通常权值矢量w的模值会很大,对导向矢量w进行二次不等式约束可有效抑制主瓣方向因此而发生的偏移问题,此时的LCMV波束形成算法可表示如下:
(12)
对于该约束方程的求解,利用Lagrange乘数法进行求解,可以将其转化为如下函数的极值问题,上述约束问题可以转化为下式关于变量w,λ,μ的最小值问题
f1(w,λ,μ)=wHRxw+λ(‖w‖2-ε)+μH(f-CHw)+(f-CHw)Hμ
(13)
式(13)中,λ为拉格朗日乘数,且满足λ≥0,Rx+λI>0,μ为拉格朗日矢量,下面对式(13)关于w的最小化求解进行分析。
1)当λ=0时,即λ(‖w‖2-ε)=0即:
f1(w,λ,μ)=wHRxw+μH(f-CHw)+
(f-CHw)Hμ
(14)
上式对于w微分,并令结果为零,可得
w=Rx-1Cμ
(15)
将w代入约束条件CHw=f,可得
μ=(CHRx-1C)-1f
(16)
由于Rx-1为接收信号的协方差矩阵,故该矩阵为Hermitian矩阵,根据矩阵的性质[Rx-1]H=Rx-1,将μ代入(15)可得最终加权矢量的表达式
w=Rx-1C(CHRx-1C)-1f
(17)
由于λ(‖w‖2-ε)=0,此时约束‖w‖2≤ε不能对权值w有效约束,导致算法的稳健性较差。
2)当λ≠0时,为了使算法具有较好的稳健性,ε应满足
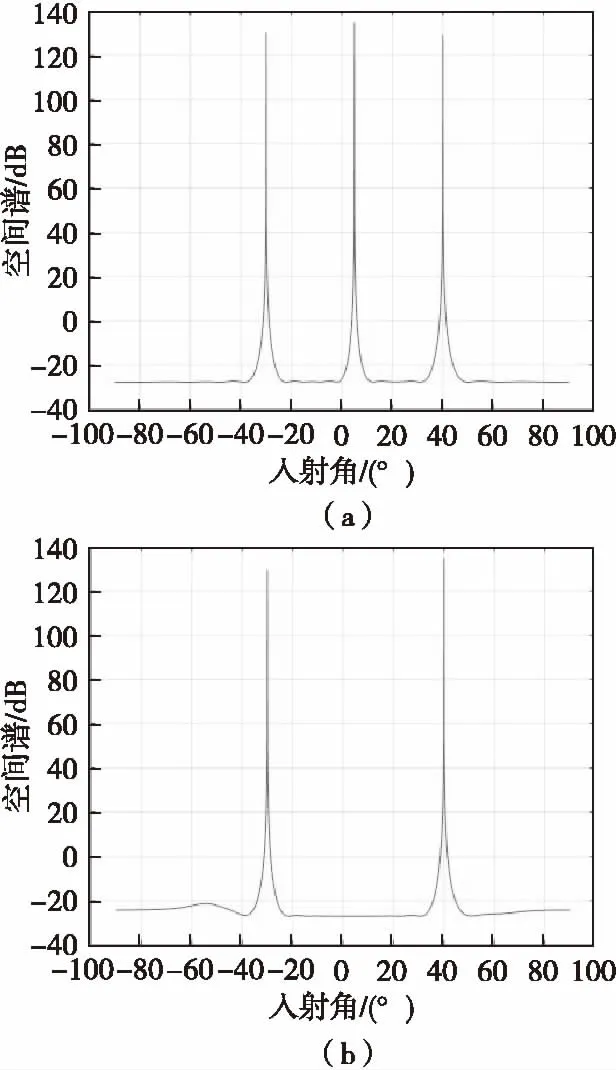
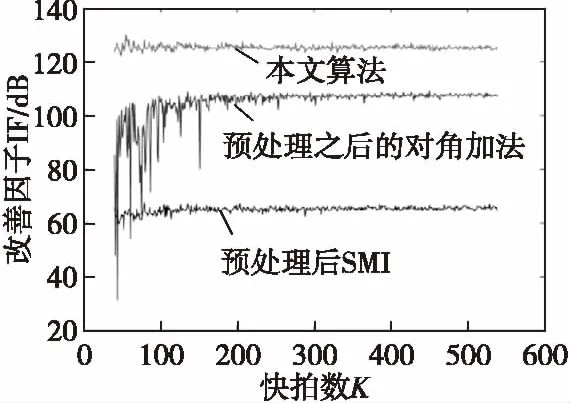
ε=wHw (18) 该条件约束着ε的上限,则 f1(w,λ,μ)=wHRxw+λ(‖w‖2-ε)+μH(f-CHw)+(f-CHw)Hμ=wH(Rx+λI)w-wHCμ-μHCHw-λε+μHf+fHμ=wH(Rx+λI)w-wHCμ-μHCHw+μHCH(Rx+λI)-1Cμ-μHCH(Rx+λI)-1Cμ-λε+μHf+fHμ= [wH(Rx+λI)-μHCH][w-(Rx+λI)-1Cμ]-μHCH(Rx+λI)-1Cμ-λε+μHf+fHμ= [w-(Rx+λI)-1Cμ]H(Rx+λI)· [w-(Rx+λI)-1Cμ]-μHCH(Rx+λI)-1Cμ-λε+μHf+fHμ (19) f2(λ,μ)=-μHCH(Rx+λI)-1Cμ-λε+μHf+fHμ (20) 对f2(λ,μ)关于μ求导 (21) 并令结果为零,可以求得 (22) 将其代入f2(λ,μ)可得 f3(λ)=-λε+fH[CH(Rx+λI)-1C]-1f (23) 上式对λ求导并令结果为零可得 ε=fH[CH(Rx+λI)-1C]-1· [CH(Rx+λI)-2C][CH(Rx+λI)-1C]-1f (24) 利用牛顿迭代法对λ其进行求解,可以求得λ的值。 (25) 可以看出上面公式和文献[7]采用对角加载项的算法所得的权值w的表达式一样,但是采用对角加载项的算法,对于加载电平的选取具有很大的主观性,选取加载电平的大小是否合适直接影响波束形成的好坏。本文通过对导向矢量进行二次不等式约束,并利用牛顿迭代法对公式(24)求出λ的值,有效地解决了波束形成的最优加权矢量的求解问题。 为了验证所提出算法的有效性,进行如下仿真实验。假设阵列为理想的均匀线性阵,阵元个数N=16,阵元间距d=λ/2。假设空间中存在一个期望信号和三个等功率互不相干的干扰信号,期望信号的方位角为0°,干扰信号的方位角分别为5°,-30°和40°,各通道内的噪声均为高斯白噪声,其中信噪比为0 dB,干噪比为40 dB,阵列采样快拍数K=500。 实验一 首先采用MUSIC算法验证了用阻塞矩阵抑制主瓣干扰的有效性。图1(a)和图1(b)分别给出了未经阻塞矩阵预处理和经阻塞矩阵预处理后,利用MUSIC算法对预处理前和预处理后空间谱估计的结果。从图中可以看出,经过阻塞矩阵处理后有效地消除了主瓣干扰的影响。 图1 利用MUSIC算法估计预处理前 和预处理后的DOA对比Fig.1 MUSIC algorithm estimation of pre-and post-pretreatment DOA comparisons 实验二 图2(a)分别给出了用LCMV算法、SMI算法和Capon算法形成的未经阻塞矩阵预处理的波束形成方向图,从图中可以看出三种算法均在干扰处形成了较深的零陷导致了主波束变形、副瓣电平升高且峰值发生偏移,这会导致输出信干噪比(SINR)下降,虚警概率上升等问题。 图2(b)给出了未经过阻塞矩阵处理和经过阻塞矩阵预处理之后利用LCMV算法波束形成后得到的方向图的对比。从图中可以看出,经过阻塞矩阵预处理之后的方向图,虽然在一定程度上解决了主波束变形和副瓣电平升高的问题,但也导致了主波束指向发生严重偏移的问题,这会严重影响后期处理的测角精度。 图2 不同波束形成算法得到的方向图Fig.2 different beamforming algorithm obtained by the direction of the map 实验三 图3分别用SMI算法、对角加法和本文提出的算法对经过阻塞矩阵预处理后的数据进行自适应波束形成的波束方向图。 图3 自适应波束方向图Fig.3 Adaptive beam pattern 从图中可以看出三种算法均在副瓣干扰的角度形成了较深的零陷,而在主瓣的位置有效抑制了干扰,克服了自适应波束形成带来的主瓣变形和副瓣电平升高等问题。但是从图中可以看出通过SMI算法得到的方向图指向和真实方向有较大的偏差,而通过采用对角加法的LCMV算法,虽然主方向指向得到很大的改善,但是副瓣电平有所提高,且存在电平加载量选取与经验有关,选取过大会导致副瓣零陷发生偏移,选取过小会导致加载量不足等问题。通过本文算法,对基于LCMV算法的导向矢量w进行二次不等式约束,然后利用本文提出的Lagrange乘数法进行求解可以精确求解出λ的值,可有效避免加载电平选取经验化问题。 实验四 图4是分别在不同的快拍下利用不同算法得到的方向图。 图4 不同快拍下波束形成方向图Fig.4 beamforming pattern under different snapshots 从图中可以看出采用对角加法的LCMV算法受快拍数影响较大,当在低快拍时该算法的副瓣发生严重变形,已经不能正常工作,而随着快拍数的增加,副瓣波束得到明显的改善。而本文的算法受快拍数影响较小,在低快拍时波束仍能保持较好的性能。 实验五 为了衡量不同算法形成的波束对噪声的抑制效果,引入抗干扰改善因子(IF)的定义: (26) 式(26)中,SINR0为经过波束形成处理后的信干噪比,SINRi为输入信号的信干噪比。由于经过预处理后,信号没有参与数据协方差R的计算,也就是说经过自适应波束形成得到的自适应权重w不会对信号相消,所以SNR0=SNRi,式(26)可写为: (27) 从图5可以看出通过SMI算法相对于另外两种算法得到的改善因子较小,也就是说输出的干噪比仍较大,效果不理想,而通过对角加法算法一定程度上使改善因子得到提高,但是改善因子在低快拍时受快拍数影响较大。通过比较可以看出本文的算法获得的改善因子较高,即使在低快拍时仍能得到较好的效果。 图5 改善因子IF随快拍数的变化Fig.5 Improve the factor with the rapid changes in the number of shots 本文提出了基于阻塞矩阵预处理的抗主瓣干扰算法,该算法利用MUSIC算法估计出主瓣干扰的角度,然后利用估计出的干扰的角度构造阻塞矩阵对主瓣干扰进行预处理,针对预处理得到的数据利用LCMV波束形成算法得到的方向图存在主瓣偏移等问题,对这一现象进行了详细的分析,最后利用对加权矢量二次不等式约束解决波束指向与信号不匹配的问题,但是对于加载电平λ的选取人为经验因素较大。对此,本文对方程中λ的求解问题提出了利用Lagrange乘数法进行求解,可以精确地求解出λ的值,最后通过仿真验证了本文提出算法的有效性。但是由于本文算法首先需要利用MUSIC算法估计出干扰所在的角度,然后利用此信息构造出阻塞矩阵,如果阵列误差估计角度较小的情况下可以取得较好的抗干扰效果,但是若阵列的估计角度存在较大误差情况下,构造的阻塞矩阵无法完全将主瓣进入的干扰阻塞掉,从而导致输出信噪比下降,为此需要进一步对算法进行优化,增强算法的鲁棒性。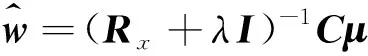

3 仿真验证



4 结论

