基于Workbench的引信动态响应仿真方法
吕铁钢,张 亚,李世中
(中北大学机电工程学院,山西 太原 030051)
0 引言
考核引信性能通常是在实弹中进行试验的,存在着费用高、危险系数大等缺点,所以模拟试验变成了一条可行的途径。随着电子信息技术的发展,通过有限元仿真软件分析,人们可以清楚地看到炮弹是如何作用的。考核引信性能,安全性与可靠性放在首位。炮弹发射过程中,由于受到膛内压力的作用,短时间内弹体会产生很大的加速度。以末制导炮弹为例,在2~3 ms内弹体与其内部构建将承受到10 000g左右的高过载。这种高过载环境为弹体结构设计带来了很大的困难,尤其是其内部精密构件的设计。美国陆军研制的激光制导“铜斑蛇”[1]炮弹不仅具有制导精度和命中概率高的特点,同时还兼备了很高的可靠性和高过载的承受能力,其内弹道轴向过载曲线如图1所示。在高过载环境下,分析引信的动态响应是其结构设计的重要条件之一。由于膛压随时间的变化先增大后减小,很难直接得到引信所承受的载荷,能得到的是构件施加给引信的加速度随时间变化的信息。本文针对此问题,提出了基于Workbench的引信动态响应仿真方法。

图1 “铜斑蛇”内弹道段轴向过载曲线Fig.1 “Copperhead” internal ballistic axial overload curve
1 建立有限元模型
1.1 结构选取与分析
制导炮弹试验弹自行设计其内外部结构[2],结合数据,对试验模型进行简化处理,引信作为武器系统发挥终端效应的最终执行装置,作用不言而喻,其上部是一些精密构件,将精密构件简化为一个质量单元,引信同时作为支撑件与被支撑件,满足的要求必须是本身结构不破坏。在火药燃烧产生的膛压作用下,试验弹受到弹底压力在膛内运动,忽略摩擦与空气阻力,引信将受到弹体施加的轴向加速度,所以说对其结构设计要求是弹体为其提供稳定的支撑,不至受到过高载荷而破损。炮弹在发射时,在膛内的加速度很高,引信内部的零件会受到强烈的冲击力[3],1 g质量的微小零件将要受到500~600 N的力。这样大的力就有可能使某些起爆原件自行发火,如果引信发火,就会引爆战斗部发生膛炸,造成武器受损、人员伤亡的严重后果。为此要合理设计弹体与引信结构。中、大口径火炮的最大后坐过载系数在1 000~30 000之间,小口径火炮的最大后坐过载系数在30 000~110 000之间。
1.2 有限元模型
仿真时把试验弹看成一个整体结构,引信作为独立在结构外的单元,在建模时,考虑到引信内部结构复杂,所以简化引信内部结构,只保留壳体。当引信作为支撑物时,建立一个大质量单元,主要分析引信动态响应;当试验弹作为支撑物时,建立另一个大质量单元,对试验弹进行模态与应力应变分析[4],所以对试验弹整体进行简化。结构动态响应分析采用Workbench有限元分析软件,
1)主要战斗技术要求,具体参数见表1。

表1 弹体、引信材料模型参数Tab.1 Projectile material model parameter
2)部位安排与结构布局
部位安排是总体设计的重要环节,就是将战斗部、引信、弹上制导设备和动力装置等进行合理的安排,由于文章采用的是试验弹,以制导炮弹为例[5],忽略内部精密结构,部位安排上,从弹头向后依次是弹头部、舵翼、舵机舱、战斗部、弹带、尾翼,在保证总体质量一定的情况下,结构采用轴对称类型。有限元分析时,为避免两体连接处发生位移,故采用螺纹连接一体结构法,这样会简化连接处刚度的变化,整体网格的划分决定了分析时误差的大小。图2为试验弹结构简图。

图2 试验弹结构简图Fig.2 Structural sketch of test missile
在建立模型之前做如下假设:
1)弹体视为一个整体,各舱段之间连接强度满足;
2)忽略膛壁对弹带的压力;
3)忽略弹托前后的紧固环,忽略舵翼、尾翼;
4)忽略温度的影响;
5)忽略其他弱境力的影响;
结构动态响应分析采用Ansys有限元软件Workbench。选取大质量单元的质量为引信结构的300倍以上,模型输入材料、参数,合理设计试验弹结构尺寸。火药燃气产生的压力作为膛压,在发射后座和旋转双环境下[6],可以通过试验和数值计算,进行仿真。图3为试验弹结构有限元网格模型,图4为引信有限元网格模型。

图3 试验弹有限元网格模型Fig.3 Mesh model

图4 引信有限元网格模型Fig.4 Finite element mesh model of fuze
模拟试验弹并不能代替真实地全弹试验,主要表现在:
1)该动态试验不能模拟过载时间的长短只能模拟过载大小;
2)不能完全考核引信的全部性能,有一定的局限性。
2 引信的模态分析
模态分析就是计算结构振动的的一些基本振型所对用的频率[7],实际工作中,为了防止共振,就要避开这些固有频率,从振态的形状我们可以计算出在某个自然共振频率下,试验弹引信结构的变形趋势。若要加强某个结构的刚性,你可以从这些较弱的部分来加强。对于模态分析,系统微分方程为:
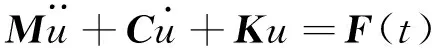
(1)
式(1)中,M为刚度矩阵、C为质量矩阵、k为阻尼矩阵、F为动态载荷列向量,这就要求材料是线弹性的、使用小位移理论(不包括非线性)。
在不考虑阻尼的情况下,系统地自由振动方程变为:

(2)
如果定义u=φsinf(t-t0),式中,φ为n阶向量,f为向量的振动频率,将其带入式(2)中,进一步简化为:
Kφ-f2mφ=0
(3)
则式(3)变为求解广义特征值的问题。
试验弹在膛内运动时,由于有弹带支撑,弹带处圆柱部被固定,可以视试验弹为悬臂梁处理。引信所选材料为材料2A12铝合金,通过在Workbench中建模、定义材料属性、定义边界条件、网格划分、输入参数并进行模态分析,最后得到引信前三阶模态分析固有频率[8],见表2。图5、图6、图7表明,引信最大振型发生的部位位于根部和颈部,所以危险截面发生在根部和颈部,然而实际振动形态并不是一个规则的状态,模态分析结果只能说明引信共振时更易于发生变形。

表2 引信前三阶模态分析结果Tab.2 Three order modal analysis results before fuze
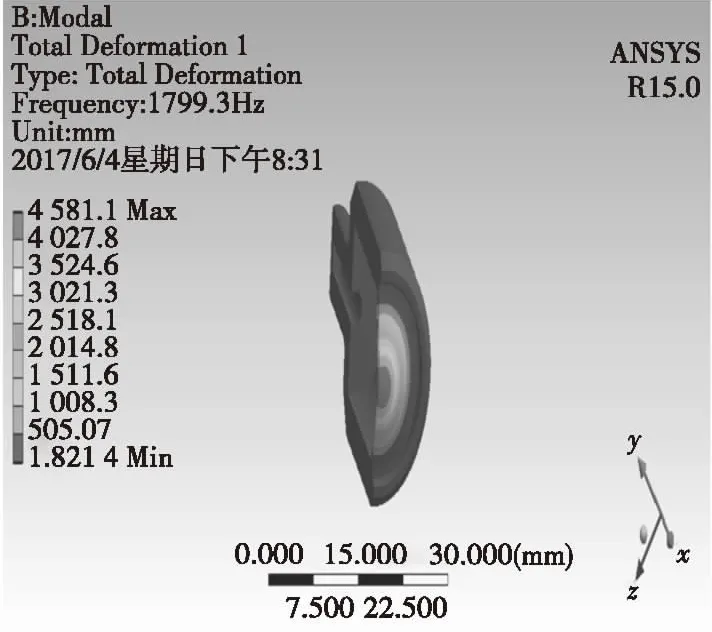
图5 引信一阶模态云图Fig.5 First order modal cloud of fuze

图6 引信二阶模态云图Fig.6 Two order modal cloud of fuze

图7 引信三阶模态云图Fig.7 Three order modal cloud of fuze
Ansys Workbench中的结构模态分析是线性的,在分析中忽略系统阻尼对其自身振动特性的影响,而且,任何所施加的力载荷在模态分析中都不考虑。设定求解参数,对试验弹进行自由模态分析求解前10阶模态,由于未施加任何位移约束,故而计算的前6阶模态都为试验弹的刚体模态,其值近似为0,如图8所示。

图8 前10阶模态计算结果Fig.8 Calculation results of the first 10 order modes
在属性栏指定计算弹体第7阶主振型,也就是其第一阶Y方向弯曲振型,以上分析可以得出引信的固有频率远远高于试验弹的固有频率[9],即引信第一阶频率为1 799.3 Hz,试验弹第一阶频率为485.45 Hz;引信第二阶频率为2 015.8 Hz,试验弹频率为490.15 Hz;引信第三阶频率为2 058.1 Hz,试验弹频率为571.23 Hz。从而推出引信可以避开试验弹的固有频率范围,即可以避免共振发生,其模态设计符合要求。
3 引信的动态响应数值分析
由于引信与基座无间隙配合,在承受加速度载荷以后,使得结构做强迫运动,将膛内时刻的强迫运动转化为载荷处理,同时计算了由膛压换算来的系统加速度,如图9所示。
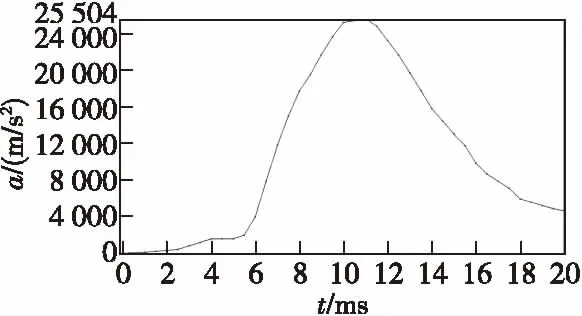
图9 按膛压换算的加速度曲线Fig.9 Acceleration curve according to chamber pressure
在理想膛内环境下,引信发射过程中主要受到膛内后坐力、弹带挤进压力、内弹道离心力以及其他弱境力,简化其受力情况,主要分析膛内后坐力。当弹带挤入膛线时[10],膛线给试验弹一个旋转力,角速度约为180 rad/s,根据分析结果可以得出,弹体受力随着炮膛内空间的变大而变大,参考膛内火药燃气压力分布规律,当火药完全燃烧结束,膛压达到最大值,同时加速度值也达到最大,随后逐渐减小,引信最大后坐过载大约3 000g,等效应力的峰值出现在根部,应力响应过程如图10所示,应力峰值在11 ms左右出现,大小为22.914 MPa,此数值并未达到材料的极限应力值(390~405 MPa),因此不会造成结构的破坏。
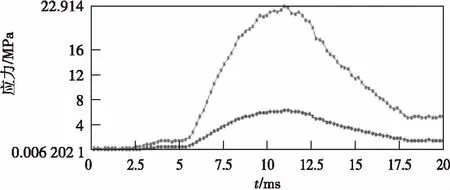
图10 引信底部节点应力变化曲线Fig.10 Stress variation curve at bottom node of fuze
4 结论
本文提出了以有限元软件模拟试验弹发射,仿真试验弹在膛内运动时引信体的应力应变分析和模态分析,可以有效的计算出引信体在工作载荷下的危险区域以及反映出弹引系统本身的振动特性。仿真结果表明在结构的高过载环境下,引信的最大应力在极限应力范围内,要求设计固定引信时采用螺栓固定,为避免引信与弹体发生共振,同时使引信前端与填充物保持一定间隙,以防发生受力形变。
模拟仿真只能作为参考,如需作为标准,还需进一步的研究。

