基于改进布谷鸟算法的分数低阶盲均衡算法

王旭光，陈 红，褚鼎立

(国防科技大学电子对抗学院，安徽 合肥 230031)

0 引言

盲均衡算法不需要训练序列，只需要依靠自身接收的信号的统计信息来更新均衡器向量，可以有效提高系统的宽带利用率[1]。由于计算量小、实时性强等优点，常模盲均衡算法(CMA，Constant Modulus Blind Equalization Algorithm)备受关注。上世纪90年代，基于CMA的分数间隔均衡器得到了广泛发展和应用[2]。CMA算法的代价函数不含相位信息，对相偏反应迟钝，仅适用于均衡幅度恒定的信号。最初的盲均衡算法研究是在无噪声的假设下进行的，这是由于当时大多数学者认为码间串扰(Intersymbol Interface，ISI)是引起通信信号失真的主要原因。这一假设对有线通信情况，如同轴电缆、光纤或双绞线是适用的，但是对于无线通信系统不合适[3]。而后，Fijalkow等人将信道噪声建模为高斯白色噪声模型，研究了加性高斯噪声信道对CMA算法的影响[4]。但是自然界中的很多噪声，如枪炮声、电器开关、雷电磁暴等，都具有很强的脉冲性，在很短时间内具有很强的幅度。而α稳定分布是唯一一种满足广义中心极限定理的分布，可以有效描述这一类噪声干扰，Nikias等人最先将其引入信号处理领域[5]。α稳定分布具有很强的代表性，可以描述各种不同类型的脉冲噪声。在这种噪声条件下，许多传统的信号处理方法性能下降严重，如CMA。因此，将CMA加以改进，使它能够在脉冲噪声环境下也有较强的适应能力，是当前一个重要的研究方向。

布谷鸟算法(Cuckoo Search，CS)是一种新式的元启发算法，一经出现就受到了国际学者的广泛关注。具有以下几个优点：操作简单、参数少，在处理优化问题时无需重新匹配参数。但是布谷鸟算法也具有收敛速度慢、容易陷入局部最优、末期缺少种群更新缓慢等缺点[6]。针对以上问题，我们将椋鸟群行为[7]引入到布谷鸟算法中,提出了一种引入椋鸟群行为的布谷鸟算法(Cuckoo Search Inspired By Starling Flock Behavior，SCS)。椋鸟群行为仿照了自然界中，椋鸟遇到天敌后，种群个体之间相互传递信息，从而迅速规避天敌的行为。当算法陷入局部最优时，根据椋鸟的集体行为更新巢，增加了变异几率，提高了搜索精度与效率。本文针对此问题，提出了基于改进布谷鸟算法的分数低阶盲均衡算法。

1 脉冲噪声与分数低阶统计量

在无线通信中，尤其是在复杂电磁环境下，信号中的噪声和干扰往往具有较强的脉冲性而且不服从高斯分布，而α稳定分布模型则更适用于描述这些噪声[8]。其特征函数为：

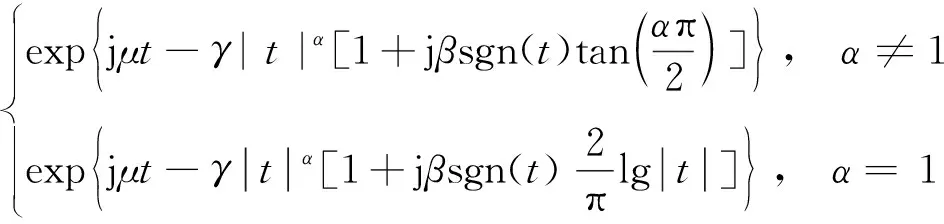
(1)

式(1)中，α是特征指数(0<α≤2)，当α=2，β=0时，式(1)可化简为φ(t)=exp(jat-γ|t|α)，此时α分布可以看作为高斯分布。此外，α越小，噪声的脉冲性就越强,γ是分散系数，又叫尺度参数，反映了α稳定分布的离散程度，其值必须取正数,β是对称系数，反映了α分布的倾斜程度，当β=0时，α稳定分布是关于μ对称的,μ是位置参数[9]。图1是一个α=1.5时的对称α稳定分布序列。

图1 α=1.5时的对称α稳定分布序列Fig.1 Symmetric alpha-stable distribution when α=1.5

当α<2时，α稳定分布不再存在二阶以及高阶统计量，这使得CMA算法在脉冲噪声条件下性能严重退化。而在α稳定分布噪声条件下，分数低阶统计量(Fractional Lower Order Statistics, FLOS)在信道均衡中可以起到抑制脉冲噪声的效果[9]。Rupi等提出了基于分数低阶统计量的常模盲均衡算法(FLOSCMA)，该算法利用输入信号的分数低阶矩设计代价函数，但是稳态误差仍比较大[9]。

2 改进的布谷鸟算法

2.1 布谷鸟算法

自然界中，有一些布谷鸟会将卵偷偷产在其他鸟的巢中，让宿主鸟替自己哺育后代,经过研究， Yang Xinshe教授和Deb教授提出了一种新型元启发式算法——布谷鸟算法(Cuckoo Search，CS)[6]。

为了易于仿照布谷鸟繁衍后代的方式，Yang教授等对其作了以下几点假设：

假设1 每一只布谷鸟一次只产一枚卵，并随机放在宿主巢中。

假设2 最优的巢(适应度最优)将被保留到下一代。

假设3 每一代巢数量是固定的，且布谷鸟卵被宿主鸟发现的概率为P∈(0,1)。

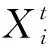
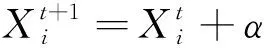
(2)

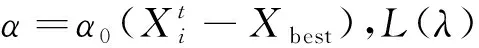
L(λ)～u=t-λ,1<λ<3

(3)

设布谷鸟蛋被宿主鸟发现的概率为Pa。经过Levy飞行后，得出一组新巢位置[X1,X2,…，XN]，此时产生随机数p∈(0,1)，若p>P，则表示宿主鸟发现布谷鸟蛋，此时布谷鸟将另外寻找一个巢产卵，位置更新公式如下[6]：

(4)

2.2 椋鸟群行为

椋鸟群经常像云团一样飞行，他们聚集起来主要是为了躲避天敌。当有威胁出现时，椋鸟群会迅速改变方向。这种改变首先从鸟群中个别个体开始，迅速传导至整个种群，使得整个种群的方向改变，从而躲避天敌。

在椋鸟群中，每一个个体的飞行方向不仅仅取决于自己，而且可以被周围的其他鸟传递的信息影响，这就会最终造成整个鸟群的方向变换。在椋鸟群中，椋鸟个体一般会与其附近的7个个体进行信息交流，这7个个体再分别与其附近的7个个体进行交流，最终可以完成整个种群的信息共享。有分析表明，6个或7个个体组成一个群体交流网络将有效平衡整个种群凝聚性及个体交流[7]。

2.3 引入椋鸟群行为的布谷鸟算法(SCS)

CS算法在搜索过程中很难收敛到全局最优，而且后期缺乏有效变异手段，搜索效率比较低。将椋鸟群行为引入到布谷鸟算法中，将有利于加大种群多样性，减少算法后期陷入局部最优的风险。为了增加向有利方向调整的概率，我们设定了一个迭代停滞上限(Max_limit)。Max_limit的大小是由经验决定的，过大则会导致算法灵敏度不高，不能有效判定是否陷入局部最优；过小则会使算法频繁被椋鸟群行为修正，影响计算效率。当算法判定陷入局部最优时，挑选一定适应度较差的巢，将这些巢的位置进行变换，然后重新计算这些巢的适应度，若优于变换前则加以替换。

其中，位置变换公式为[10]：

(5)

(6)

若得出更新后的适应度值优于原始巢，则加以替换，反之维持原巢。

以上述公式和假设为基础，SCS算法步骤描述如下：

Step1：初始化目标函数f(X)，其中X=(x1,x2，…，xd)，种群数n，布谷鸟蛋被发现的概率P，最大迭代次数N_iter，迭代停滞参数count=0，迭代停滞上限Max_limit，算法终止门限，巢位置上下限Ub，Lb，初始化n个鸟巢的位置(X1,X2,…，Xn)，并确保其在上下限范围里。

Step2：计算每个鸟巢的适应度值，并找出当前最优解以及所对应的巢。

Step3：保留最优巢，利用Levy飞行得到一组新巢。

Step4：将Step3中得到的新解与上一代的一一对比，保留适应度最优的，进入下一步。

Step5：生成一个随机数p∈(0，1)，若p>P，则此巢中蛋被宿主发现，布谷鸟利用公式(4)寻找一个新巢；否则保持不变。将更新后的鸟巢与上一步得到的最优解比较，选取较优解。若前后两者适应度值没有变化或者变化不大，则迭代停滞参数count+1(初始值为0)；若有较明显变化，则count置零。

Step6：判断count是否大于Max_limit，若大于则从种群中挑选出适应度较差的num个个体，利用式(9)更新鸟巢的位置，然后与原种群比较，替换掉适应度差的个体，count置零；若小于则进入Step7。

Step7：当超出算法终止门限或达到最大迭代次数时，回到Step3；否则跳出并输出[11]。

3 基于改进布谷鸟算法的分数低阶常模盲均衡算法

针对条件下的传统盲均衡算法稳态误差过大的问题，文献[10]提出了FLOSCMA算法， 该算法利用了信号的分数低阶恒模特性设计代价函数，在脉冲条件下该算法具有很好的适应性但是收敛速度缓慢。为了提高α稳定分布噪声条件下盲均衡算法的性能，本文将SCS算法引入到FLOSCMA，将均衡器权向量建模为SCS算法的宿主巢，将FLOSCMA的代价函数加以改进，作为SCS算法的适应度函数，将均衡器输入信号作为SCS算法的输入。然后让SCS算法在一定范围内寻找FLOSCMA代价函数的最优解或其附近的解，并找到对应的巢作为均衡器的初始权向量，然后再利用FLOSCMA算法精确搜索。SCS-FLOSCMA算法框图如图2所示。

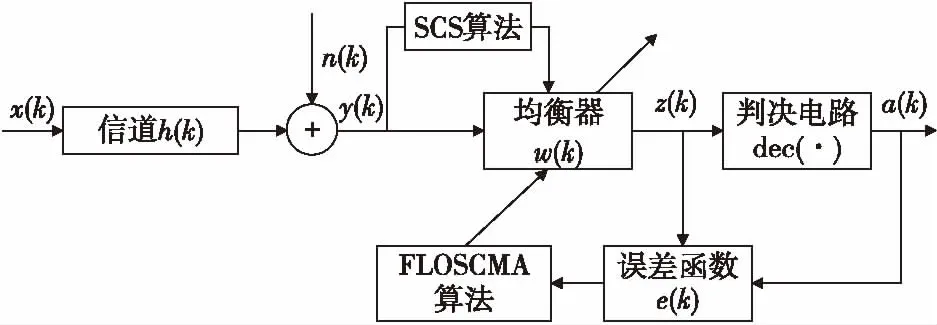
图2 SCS-FLOSCMA算法流程图Fig.2 The flow chart of SCS-FLOSCMA

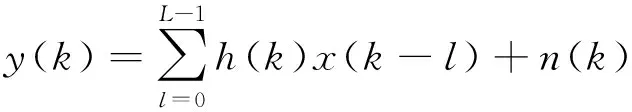
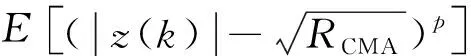
(7)

利用JFLOSCMA可以得到SCS算法的适应度函数为：

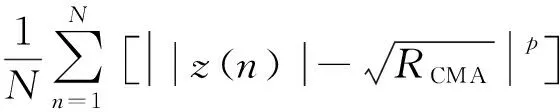
(8)

这样就可以利用SCS算法来求得JFLOSCMA的最小值，进而求出所对应的均衡器权向量。然后，将SCS算法得到的最优巢位置作为初始权向量，再利用FLOSCMA算法精确求解。

根据随机梯度下降法，得到FLOSCMA算法的均衡器权向量更新公式为[12]：

(9)

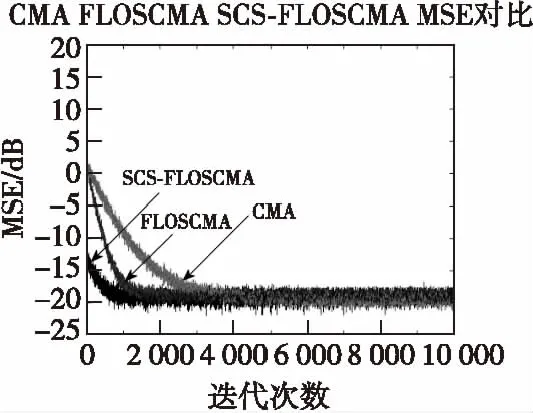
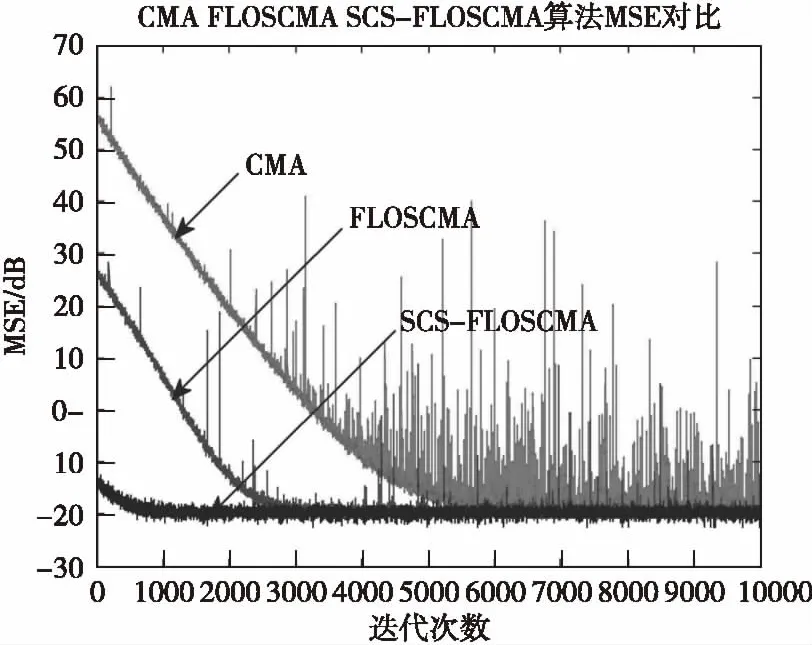
式(9)中，μ为步长，p(0

通过以上分析可以看出，SCS-FLOSCMA算法首先依靠SCS算法在一定搜索范围内进行搜索，得到一个靠近最优解的次最佳解作为FLOSCMA的初始权向量，然后再依靠FLOSCMA进行精确搜索，以提高算法的收敛速度，并有助于使剩余稳态误差更稳定。

4 仿真实验与结果分析

为了验证SCS-FLOSCMA性能稳定性，将CMA、FLOSCMA、SCS-FLOSCMA做对比，仿真平台为Matlab R2014a。

仿真一：在高斯噪声下，比较CMA算法、FLOSCMA算法、SCS-FLOSCMA算法的性能，采用水声信道h=[0.313 2，-0.104 0,0.890 8,0.313 4]，发射信号为4 000点的4QAM信号，信噪比为SNR=20 dB，均衡器长度为7，CMA、FLOSCMA、SCS-FLOSCMA迭代步长均为μ=0.001，低阶统计量p=1.7，SCS-FLOSCMA算法中种群数量均为20，最大迭代次数300，判决门限为适应度fit≤0.1，迭代停滞上限Max_limit=5，发现概率为Pa=0.25，特征指数α=1.5，蒙特卡洛400次仿真结果如图3所示。

图3表明，当环境噪声为高斯噪声时，CMA算法、FLOSCMA算法、SCS-FLOSCMA算法最后均可以达到理想的均衡效果。而SCS-FLOSCMA算法可以最快收敛，CMA算法收敛速度则最慢。

图3 高斯噪声环境下均方误差曲线Fig.3 Curve of mean square error under gaussian noise

仿真二：在α稳定分布噪声中，比较CMA算法、FLOSCMA算法、SCS-FLOSCMA算法的性能。采用广义信噪比GSNR来衡量信号与脉冲噪声之间的强弱关系，如式(10)所示[13]：

GSNR=10lg(E(|y(k)|2)/γ)

(10)

仿真实验中取GSNR=25 dB，均衡器长度为7，CMA、FLOSCMA、SCS-FLOSCMA迭代步长均为μ=0.001， SCS-FLOSCMA算法中种群数量为20，最大迭代次数300，判决门限为适应度fit≤0.1，迭代停滞上限Max_limit=5，发现概率为Pa=0.25，脉冲噪声的特征指数α=1.7，β=a=0，蒙特卡洛400次仿真结果如图4、图5所示。

图4 三种算法星座图Fig.4 Constellation of CMA、FLOSCMA and SCS-FLOSCMA

图5 脉冲噪声环境下均方误差曲线Fig.5 Curve of mean square error impulse noise

从图4、图5可以看出，在脉冲噪声环境下，CMA不能达到理想均衡效果，如图4、图5所示，其均方误差曲线波动极大，而FLOSCMA、SCS-FLOSCMA则相对来说可以有效收敛。其中SCS-FLOSCMA星座图中点最集中，收敛速度最快且均方误差曲线最平稳。所以SCS-FLOSCMA算法可以在α稳定分布噪声环境下很好的工作，在不同噪声环境下适应力都较强。

5 结论

本文提出了基于改进布谷鸟算法的分数低阶盲均衡算法。该算法改进CS算法，引入了椋鸟群行为，增大了CS的搜索效率，可以使得算法有效收敛至全局最优；然后考虑FLOSCMA的特点，将其代价函数加以修正，作为SCS的适应度函数，将巢作为FLOSCMA的初始权向量，并进行精细搜索。仿真表明，该算法在不同噪声环境下均能有效工作，特别在脉冲噪声环境下，稳态误差以及收敛速率要明显优于CMA、FLOSCMA。