改进的正交补空间匹配追踪算法
苗英杰,崔 琛,易仁杰
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
压缩感知理论[1-3](Compressed Sensing,CS)是近些年被提出的一种信号处理理论,它突破了传统的奈奎斯特采样定理的限制,充分利用了信号的稀疏性来获取和处理信号[4]。作为一种新的信号处理理论,为信号的数字化过程提供了一种新的选择。CS理论指出:如果信号是稀疏的或可压缩的,便可以利用特定的观测矩阵将高维信号线性投影到一个低维空间,并且不会造成信号中的重要信息丢失,最后通过求解一个优化问题可以从低维观测向量中高概率精确重构出原始信号。目前CS理论的研究主要集中在信号的稀疏变换、观测矩阵设计和信号重构等方面,其中重构算法关系到信号重构精度的高低、时间开销的大小。重构性能的好坏直接影响着压缩感知的实用性。
目前重构算法主要分为三类[5]:凸松弛算法、贪婪算法和组合算法。凸松弛重构算法重构效果好,但是计算复杂度高,导致重构时间较长;组合算法重构时间短,但重构结果不够准确;贪婪算法兼顾了运行效率与重构精度,因其算法结构简单、运算量小等特点受到青睐。在近些年诸多学者的研究中逐步的发展和完善,同时衍生出了一系列的改进算法。贪婪类重构算法中的补空间匹配追踪[6-7](Complementary Matching Pursuit,CMP)是针对匹配追踪[8](Matching Pursuit,MP)算法信号重建误差过大的问题提出的一种改进算法。CMP算法不同于MP算法,它是在系数空间而不是在信号空间实现的,可以获得比MP算法更稀疏、误差更小的逼近信号。正交补空间匹配追踪(Orthogonal Complementary Matching Pursuit,OCMP)算法是在CMP算法基础上的一种改进,类似于OMP[9](Orthogonal Matching Pursuit,OMP)针对MP算法的改进。本文根据上述研究,提出了改进的正交补空间匹配追踪算法。
1 压缩感知理论
假设离散信号x∈RN×1中至多含有K个非零值,即‖x‖0≤K,如果满足K≪N,则称信号x为K-稀疏的。然而在实际应用中的信号x本身一般是非稀疏的,但是对x在某个变换域Ψ∈RN×N中做如下变换:
(1)
如果稀疏s∈RN×1中最多含有K个非零值,且K≪N,则称s为稀疏表示系数,与之对应的x也被称为K-稀疏信号,Ψ被称为稀疏基。
针对信号x,CS利用符合一定条件的观测矩阵将高维信号投影到低维空间中,观测过程如下式:
y=Φx=ΦΨs=Θs
(2)
式(2)中,x为原始信号,s为x在稀疏基Ψ下的稀疏表示系数,Φ∈RM×N为观测矩阵,y∈RM×1为观测向量,Θ=ΦΨ称为感知矩阵。
由观测向量y求解出稀疏表示系数s的过程称为重构。如何从观测向量y中求解出稀疏表示系数s,间接得到原始信号x正是本文要解决的问题,此问题的求解通常采用如下最优化问题求解:
(3)
考虑到实际中允许存在一定程度的误差,求解式(3)的最优化问题可用一个简单的近似求解形式替代,如式(4),其中e是一个非常小的常量:
(4)
式(3)和式(4)的求解本质上是L0范数最小化求解问题,是NP难问题,无法直接求解,但是因为信号具有一定的稀疏性,这就为问题的求解提供了可能。当前这类问题的求解方法比较多,其中贪婪算法因算法结构简单、运算量小而颇受关注。
2 改进的OCMP算法
2.1 OCMP算法介绍
OCMP算法是在CMP算法基础上改进的一种算法。CMP算法类似于MP,但是与其不同的是CMP算法直接在原始信号x的行空间上进行求解。在每次迭代中,MP算法是从观测矩阵中选择一个最匹配的原子;而CMP算法则是删除(N-1)个不匹配的原子并保留剩下的一个最匹配的原子。CMP算法对观测矩阵进行了变换,此时算法求解空间不是在观测矩阵张成的M维空间,而是位于信号x所在的N维空间,因此在原子选择方式上CMP算法要比MP算法复杂。尽管从观测矩阵选择行空间上的解并不一定是最优的,残差不一定与所选原子正交,但是文献[10]中仿真实验结果表明,相比于MP算法,通过CMP算法重构出的信号稀疏性更好、误差更小。OCMP算法是针对CMP所选原子不具有正交性的特点,结合OMP算法正交化思想提出的一种改进算法,从而使算法在后续迭代中不会选择已经选择过的原子,保证了所选原子的最优性。
OCMP算法在原子选择上与CMP算法一样,然后通过选定的支撑集采用最小二乘法求解信号。假设原始信号x是稀疏的,此时稀疏变换矩阵可以看作单位阵,算法的步骤如下:
输入:稀疏度K,感知矩阵Θ∈RM×N,观测向量y∈RM×1。
初始化:初始化迭代次数t=1,重构残差rt=y,支撑集Λ0=∅,新感知矩阵F=Θ†Θ,新测量信号x′=Θ†y,其中Θ†=ΘT(ΘΘT)-1为Θ的伪逆。
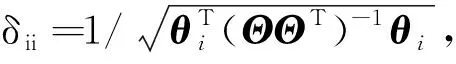
步骤2)计算新感知矩阵各原子与当前重构残差的相关性p=ΔΘT(ΘΘT)-1rt。
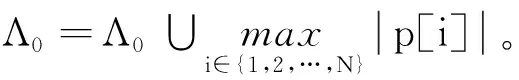
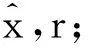
从上文可以看出,算法主要分为三部分:相关性计算、更新支撑集和计算残差。算法在每次迭代时只找到一个原子添加到支撑集,对于稀疏度为K的信号,至少需要K次迭代才能恢复出原始信号。当稀疏度K较大时,需要的重构时间更长;如果在前期的迭代循环中有错选的原子,在后续的过程中将一直存在,对信号的重构性能造成影响。
2.2 OCMP算法改进
2.2.1阈值设置
OCMP算法在迭代过程中每次选择一个原子扩充到支撑集,对于K稀疏信号至少需要K次迭代才可以完成信号的重构,当信号的稀疏度较大时则需要更多的迭代次数,算法重构所需的时间也会大大增加。针对这一问题,本文算法利用模糊阈值法进行支撑集原子的筛选。在每次迭代计算得到的内积向量中,以最大值的α倍作为阈值γ0,在内积向量中找到数值大于阈值γ0的原子集即S={|p[i]|≥α·|pmax|,i=1,2,…,N},并对该原子集中的元素求均值即γ=sum(|S|)/L(S)(sum(|S|)表示原子集S中所有元素的绝对值之和,L(S)表示原子集S的长度),以计算结果γ作为筛选支撑集原子的阈值,选出符合条件的原子加入支撑集进行信号的重构。其中0<α≤1,α值的选择由经验确定,取值过大,通过阈值γ0筛选得到的原子集原子过少,导致阈值γ过大,达不到原子筛选的目的;α的取值过小,通过阈值γ0筛选得到的原子集原子较多,引入部分相关性较小的原子,使得阈值γ的值较小,导致支撑集原子的筛选中引入过多的不匹配原子,增加算法的运算量,对信号的重构精度也会造成一定的影响。

2.2.2二次筛选
OCMP算法每次筛选出一个原子加入支撑集,在后续的迭代中只是不断的加入新的原子向真实支撑集逼近,对于错误匹配的原子,则将会一直存在支撑集中,对信号的重构性能造成影响。针对这一问题,改进算法引入回溯筛选[11-13]的思想:算法在每次迭代中选择符合条件的若干个原子加入支撑集Λ0,当支撑集的原子数大于K时,说明当前支撑集中一定有错误选择的原子,则选取当前的信号稀疏逼近结果x0中绝对值最大的K个分量对应的原子,将其余原子从支撑集中删除,支撑集Λ0中只保留这K个原子。再用修正后的支撑集求取所要恢复的信号的近似解,重新计算重构残差,若达不到迭代终止条件,则在后续的迭代过程中继续向支撑集中加入符合条件的原子,同时进行上述支撑集修正过程,直到达到迭代终止条件或完成预设迭代次数后跳出循环并输出重构信号。该方法保证了所选原子的准确性,从而保证了算法的重构精度,进一步提高信号的成功重构概率。
2.2.3改进算法步骤
改进的OCMP算法步骤如下:
输入:稀疏度K,感知矩阵Θ∈RM×N,观测向量y∈RM×1。
初始化:初始化迭代次数t=1,重构残差rt=y,支撑集Λ0=∅,新感知矩阵F=Θ†Θ,新测量信号x′=Θ†y,其中Θ†=ΘT(ΘΘT)-1为Θ的伪逆。
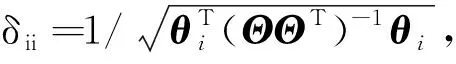
步骤2)计算新感知矩阵各原子与当前重构残差的相关性p=ΔΘT(ΘΘT)-1rt。

步骤4)由最小二乘法求信号的近似解x0=(FΛ0)†x′。
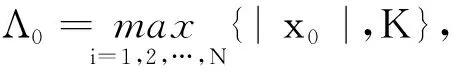
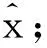
3 仿真实验及结果分析
为检验本文所提算法的重构性能,实验中将OCMP算法和改进算法进行对比,算法在ThinkPad E450机器上运行,软件版本为Matlab R2015a。实验以重构残差‖r‖2<10-6作为迭代终止条件,以随机产生的、稀疏的离散高斯信号为原始信号,设信号长度N=256,以M×N维的高斯随机矩阵作为观测矩阵[14](此时稀疏字典可以看作是一个单位矩阵,观测矩阵与传感矩阵相同)。
实验一α不同取值时算法重构性能对比
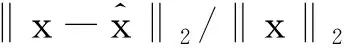
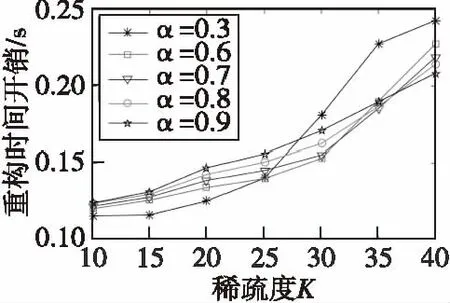
图1 不同α值对应的算法重构时间开销Fig.1 The algorithm reconstruction time cost for differentαvalues
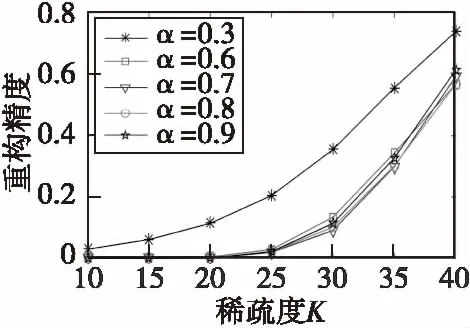
图2 不同α值对应的算法重构精度Fig.2 The accuracy of algorithm reconstruction for differentαvalues
从图1和图2中可以看出,当α取值较小时,算法的重构精度较差;当α取值较大时,算法的时间开销较大。为了兼顾算法重构精度与重构速度,本文将α值取为0.7。如果在允许牺牲一定重构精度的情况下,可以通过适当减小α的取值来扩大每次迭代中支撑集增加的原子数目,加快信号的重构速度。
实验二不同稀疏度下信号重构成功概率对比
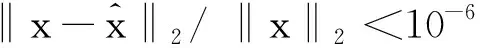

图3 不同稀疏度下的信号重构成功概率对比Fig.3 The probability of success in refactoring compared for different sparse degree
从图3中可以看出,在不同的稀疏度下,改进算法的重构成功概率相比于原始算法都有所提高,特别是在稀疏度在25~35的范围内,重构成功概率基本可以提高20%左右。其原因是在稀疏度比较低时,改进算法和原始算法基本都可以达到预设的成功重构判决条件,因此在稀疏度小于25时,两算法的成功重构概率相差不大;在稀疏度保持一定水平时,改进算法中引入对支撑集原子的二次筛选过程,使得对支撑集的估计更加精确,重构误差更小,可以更大程度的满足成功重构的条件;在稀疏度较大时,原算法与改进算法的重构误差都比较大,很难达到成功重构的条件,但是改进算法的支撑集更加接近真实支撑集,所以图3中稀疏度大于35时,虽然改进算法与原始算法的成功重构概率相差不大,但也略有优势。
实验三不同观测长度下信号重构成功概率对比
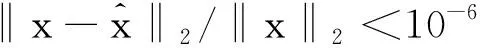
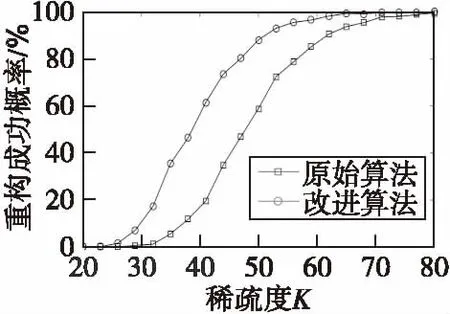
图4 不同观测长度下的信号重构成功概率对比Fig.4 The probability of success in refactoring compared for different measurement lengths
从图4中可以看出,在不同的观测长度下,改进算法的重构成功概率相比于原始算法都有较大的提升,特别是观测长度M在40~50范围内,重构成功概率基本可以提高20%左右。这是因为改进算法在信号重构的过程中引入了支撑集原子的二次筛选过程,使算法在迭代过程中更加精确的估计真实的支撑集,重构结果更加的接近真实信号,更大概率的达到预设的重构成功的判决条件。
实验四算法重构时间开销对比
图5是在观测长度M=80,稀疏度变化的情况下,进行1 000次蒙特卡洛实验,OCMP算法和改进算法信号重构所用时间的平均值。
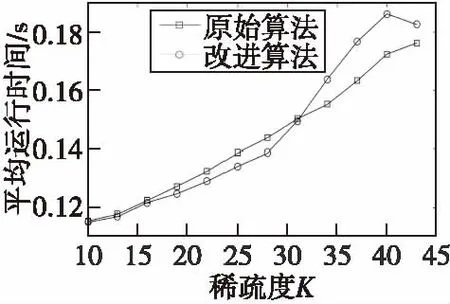
图5 算法运行时间对比Fig.5 The contrast of algorithm run time
从图5中可以看出在稀疏度K<30时,改进算法重构所需时间开销相对于原始算法有所改善,这是因为改进算法在每次迭代进行支撑集原子选择时,满足阈值的原子数目有时会多于1,这就会使改进算法比原始算法更快的完成信号重构所需支撑集的建立,只需要更少的迭代次数便可以完成信号重构;在稀疏度K>30,改进算法重构所需时间多于原始算法,这是因为在M=80,K>30时,原始算法与改进算法的重构成功概率急剧下降,信号在重构过程中若始终无法达到迭代终止条件,则强制性使算法完成预先设置的迭代次数才会终止,但改进算法相对于原始算法多了模糊阈值计算和二次筛选过程,所以会使得重构时间开销增大,出现改进算法重构时间长于原始算法重构时间的情况。
由以上三个仿真实验结果分析可知,改进算法在重构时间开销、重构成功概率等方面相对于OCMP算法都有一定的优势。在信号的稀疏程度较低时,改进算法的成功重构概率仍要高于原算法,但是时间开销会略有增加。
4 结论
本文提出了改进的正交补空间匹配追踪算法。该算法相对于OCMP算法具有更高的重构成功概率,成功重构所需的运行时间有所减少。

