基于改进鲸鱼优化算法的盲源分离方法
褚鼎立,陈 红,宣章健
(国防科技大学电子对抗学院, 安徽 合肥 230037)
0 引言
盲源分离(Blind Signal Separation,BSS)是20世纪出现的新研究领域,在对源信号和传输通道几乎没有可利用信息的情况下,仅从观测到的混合信号中提取或恢复源信号各分量的一种信号处理方法[1]。盲信号分离,本质上就是一种信号处理方式,适用于各个信息领域,其中包括无线通信、图像处理、语音识别等。当前,盲信号分离受到各国学者的关注和讨论,已经成为研究的热点与重点,尤其在信号处理、人工神经网络等方面[2],具有极为重要的研究价值。
盲处理的方法是依据一定的独立性准则构造目标函数的无监督学习方法。针对目标函数的计算法方法,文献[3]提出了随机梯度法,由于算法需要对矩阵求逆,计算量大,当矩阵奇异时,计算不稳定;文献[4]提出了自然梯度法,相较于随机梯度法更稳定,但计算量仍很大,收敛性有待改进[5];文献[6]提出了FastICA方法,计算量更少,但存在对初始值敏感的问题,导致算法不稳定。文献[7]提出基于粒子群算法的盲分离方法,该方法不易陷入局部极值,但参数设置较多、收敛速度较慢,针对粒子群算法存在的问题,本文对鲸鱼优化算法[8]进行改进,并应用于盲源分离。
1 盲分离问题描述
假设:x(t)是n个未知的相互统计独立的源信号s(t)的线性组合,即:
x(t)=As(t)
(1)
式(1)中,x(t)=[x1(t),x2(t),…,xm(t)]T,s(t)=[s1(t),s2(t),…,sn(t)]T,A为m×n阶未知混合矩阵。由于A和s未知,盲分离要通过特定算法来实现x(t)的处理,从而获得n×m阶的分离矩阵,用W表示,使得输出信号:
y(t)=Wx(t)=WAs(t)
(2)
就是s(t)的估计值。
由于s(t)和A未知,盲源分离依据条件和要求,将s(t)从观测信号x(t)中将源信号分离出来,使得最终分离出的信号无限逼近于源信号s(t),即通过分离矩阵W来实现盲源分离。一些混合信号中含有噪声成分,在处理这类信号的过程中,可以将混合信号和噪声区别开来,分别看作是不同路信号。
为了保证盲源分离的可能性,需要一些假设条件,通常为[9]:
1) 满秩混合矩阵A,源信号数不得超过观测信号数(即n≤m)。
2)基于统计要求,各源信号相互统计独立。在实际应用中,这个假设也是合理的。
3)至多有一个信号是高斯分布。
在缺乏源信号和信息通道的情况下,经过盲分离的信号并不能确定幅值和排列顺序,这一特征称为模糊性。模糊性虽然存在,但是却并不会影响最终结果[10]。
根据大数定理,多个相互独立的随机变量之和趋向于高斯分布。因此,如果观测信号是源信号的线性组合,那么源信号的非高斯性比观测信号的非高斯性更强。根据这个原理,可以通过对分离信号的非高斯性判断来确定其相互独立性[11]。分离信号非高斯性越大,其分离效果越好。
由于粒子群算法存在参数复杂、收敛速度慢等问题,本文提出利用改进的鲸鱼优化算法对目标函数进行优化的算法,旨在进一步提升对线性瞬时混叠信号的分离性能和收敛速度。
2 基于改进鲸鱼优化算法的盲分离
2.1 鲸鱼优化算法
鲸是世界上最大的哺乳动物,它的大脑构造同人脑相似,都具有梭形细胞,该细胞具有情感表达、行为判断等功能,使得鲸鱼与其他生物不同。座头鲸捕食时会群聚在一起,吐出一串串泡泡,形成一张泡泡网,合作捕食。2016年,Mirjalili S等学者[8]从座头鲸捕食行为中获得灵感,设计出一种新型算法,即鲸鱼优化算法(Whale Optimization Algorithm, WOA),该算法具备一定的自然灵感。具体来说,上述算法对座头鲸的捕食行为进行模仿,采取“螺旋气泡网”策略,即逐步缩小捕食范围、更新捕食位置,具备结构简便、调节参数减少等优势。算法数学模型有三种:一是包围猎物,二是发泡网攻击,三是搜索捕食。每次位置更新时,每个个体按照一定的准则选择其中一种更新方式。下面是三种更新方式的介绍。
2.1.1包围猎物
座头鲸能够识别猎物的位置并包围他们。由于最优位置的搜索空间不是预先知道的,WOA算法假设当前最佳的候选解是目标猎物位置或最接近目标猎物的位置,在定义最佳代理之后,其他搜索代理将向最佳代理靠近,其位置更新的数学表达式为
X(j+1)=X(j)-A·D
(3)
D=|C·X*(j)-X(j)|
(4)
式(3)、式(4)中,A和C为系数变量;X*(j)为当前最佳鲸鱼位置;X(j)表示当前鲸鱼位置;j表示迭代次数。
计算系数变量A和C:
A=2a×r-a
(5)
C=2r
(6)

2.1.2发泡网攻击
为了模拟座头鲸吐气泡捕食行为,数学模型为:
1)收缩包围:即减少式(5)中的a值。在这个过程中,A的取值范围是[-a,a],一旦这个范围发生变动,a也会相应的改变,若A在[-1,1]范围内,鲸鱼的目标位置将确定在当前位置和猎物位置之间,这表现出座头鲸的局部搜索能力。
2)螺旋式位置更新:通过计算得鲸群个体和猎物的准确具体,并将螺旋式数学模型引入:
X(j+1)=D′eblcos(2πl)+X*(j)
(7)
(8)
式(7)、式(8)中,D′为表示的是第i头鲸当前最佳位置和猎物之间的距离,b为对数螺旋形状常数;l是[-1,1]上的随机数。
座头鲸在捕杀猎物时不仅以螺旋形状游向猎物,还要收缩包围圈,以50%的概率作为阈值来更新鲸鱼位置。公式为:
(9)
式(9)中,p为[0,1]上的随机数。
2.1.3搜索捕食
座头鲸除了选择气泡网法搜索策略之外,随机搜索捕食也是一种重要手段。实际上,鲸群个体可以在彼此的距离范围内,随机捕食猎物。所以,若果A超出[-1,1]范围,距离数据D随机更新,鲸为了找寻猎物,就会偏离原本的目标猎物,使得捕食能力提高,使得WOA有一定的全局搜索性能。公式为:
D=|C·Xrand-X(j)|
(10)
X(j+1)=Xrand-A·D
(11)
式(10)、式(11)中,Xrand为当前鲸群中随机个体的位置。
2.2 自适应权重
惯性权重在粒子群算法中有重要作用,权重较大时,算法可以搜索较大的区域,收敛速度会加快;权重较小时,搜索更加精细,不易错过最优解。
受文献[12]的启发,对鲸鱼优化算法引入自适应权重,权值计算公式如下:
(12)
式(12)中,j为当前迭代次数,M为最大迭代次数。文献[12]将权重引入到式(3),如下所示:
X(j+1)=ω·X(j)-A·D
(13)
笔者认为此法欠妥,若将权重因子引入到鲸鱼的当前位置上,不符合智能优化的初衷,故将其与距离数据D结合,可以通过迭代的次数来调整收敛的速度,改进公式如下
X(j+1)=X(j)-ω·A·D
(14)
由于自适应权重对局部搜索作用明显,而式(3)和式(7)都是用于进行局部搜索的,所以将权重也同时引入到式(7)中,如下所示
X(j+1)=ω·D′eblcos(2πl)+X*(j)
(15)
2.3 分离原理
为分离混合信号x(t),本文选择通过引入自适应权重的WOA算法,来计算式(2)中的W。根据随机变量间的独立性准则,确定盲源分离方法,求得分离矩阵W,常用的有最小互信息准则、信息最大化准则、非高斯最大化准则等。在此,以文献[13]给出的四阶累积量(峰度)准则来建立目标函数,采用分离信号峰度作为信号分离的度量。
随机变量yi的峰度可表示为
(16)
如果K(yi)>0,信号yi(t)满足超高斯分布的条件;如果K(yi)=0,信号yi(t)满足高斯分布的条件;如果K(yi)<0,信号yi(t)满足亚高斯分布的条件。综合来说,非高斯性和峰度的绝对值之间成正比。所以,峰度最大,也就意味着超高斯信号的存在,足以说明信号分离效果理想;峰值最小,也就意味着亚高斯信号的存在,信号具有分离的可能性。
对n=2的二维混合模型进行分析和说明,可以通过峰度信息来判定分离信号的有效性。假设源信号为方差等于1的非高斯信号,用s=[s1,s2]表示,s1,s2为随机变量,设其峰度为K(s1)>0,K(s2)>0;对x进行中心化、白化处理;基于此,以分离信号y=Wx为方差有限信号为假设前提,不妨设E(yyT)=I;则分离信号的第i个分量为
yi=Wix=WiAs=us=ui1s1+ui2s2
(17)
式(17)中,Wi为分离矩阵W的第i行。根据峰度的性质,可知
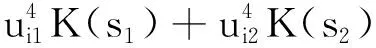
(18)

为了实现超高斯和亚高斯信号的分离,选择分离信号峰度的绝对值作为分离的度量:
(19)
定义目标函数为
(20)
在E(yyT)=I的条件下,
(21)
前文的假设“分离信号y=Wx为方差有限信号”是有必要的,在模糊性的影响下,盲源分离并不能获得准确的信号幅度,分离矩阵W中的全部元素同时扩大k数,分离信号y也得到相同倍数的扩大,但盲源分离信号依然准确,此时的K(y)扩大倍数却是k4倍。由此说明,若是没有上述假设的限制,式(19)没有最大值。假设E(yyT)=I,在均值、白化的处理之下,可知E(xxT)=I,使得
E(yyT)=E(WxxTWT)=E(WWT)=I
(22)

定义了代价函数式(20)之后,为了求得J(W)的极小值,采用改进的鲸鱼优化算法来对代价函数式(20)进行优化。
2.4 算法步骤
分离矩阵W为一正交阵,对于一个正交阵,可表示成一系列旋转矩阵的乘积,以n=3为例,W可表示为:

(23)
式(23)中,θ1,θ2,θ3∈[0,2π)它们分别代表3个不同的旋转矩阵的旋转角度。
以信号峰度为目标函数,基于改进鲸鱼优化算法的盲源分离方法步骤如下(以n=3为例):
1)收集并采样观测信号,对其进行中心化、预白化处理。
2)WOA算法参数初始化。将旋转矩阵的旋转角度θ=[θ1,θ2,θ3]作为鲸鱼个体的位置信息X=[X1,X2,X3],在求解空间[0,2π)内,随机确定鲸鱼位置并初始化WOA参数,包括种群数目N、最大迭代次数M、对数螺旋形状常数b、随机数l、当前迭代次数j及算法终止条件。
3)通过式(20),计算适应度Fit(W)=J(W),找到并保存群体中最佳鲸鱼个体位置X*。
4)若j≤M,更新a、A、C、l和p。
5)当p<0.5时,若A<1,通过式(14),重新确定鲸鱼位置;如果A≥1,需要在当前群体范围内随机确定鲸鱼个体位置Xrand,通过式(11),更新当前鲸鱼位置。
6)如果p≥0.5,通过式(15)重新确定鲸鱼个体位置。
7)通过式(20),计算出个体适应度Fit(W),确定群体中最佳鲸鱼个体X*。如果算法满足终止条件,就到步骤8);反之,令j=j+1,重复步骤4)~7),直到满足条件为止。
8)输出最优个体位置X*并通过式(23)计算分离矩阵W。
9)利用得到的分离矩阵W通过式(2)估计出源信号。
3 仿真验证
本节基于Matlab2014a平台仿真验证并分析基于改进鲸鱼优化算法的盲信号分离性能。仿真实验如下。
实验一:无噪情况下,采用三路仿真信号作为源信号,采样频率为3 000 Hz,共使用500个采样点。三路仿真信号分别为符号函数、幅度调制信号、正弦信号,当t从1遍历到500时,生成信号如下:
它们的峰度分别为-2.000 0,-0.050 3,-0.375 0,三路信号瞬时混合,混叠矩阵取为:

在分离混合信号时,选择鲸鱼优化算法,鲸鱼的种群数目取30,迭代次数取50,鲸鱼位置信息区间为[0,2π),为了证明鲸鱼算法的效果,与基于粒子群算法的盲源分离做了对比实验,为了方便比较,粒子数取为30,迭代次数也为50,两个学习因子都设为0.8,仿真结果如图1—图5所示。
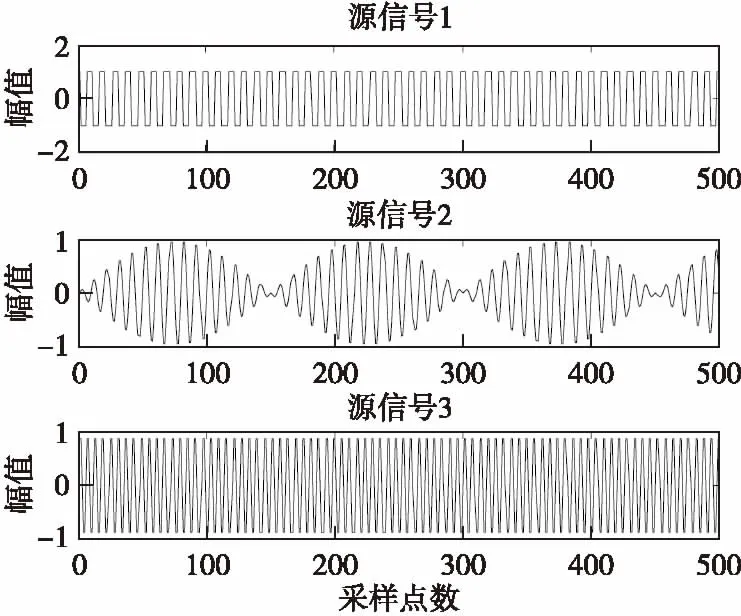
图1 源信号Fig.1 Source signals

图2 混合信号Fig.2 Mixed signals
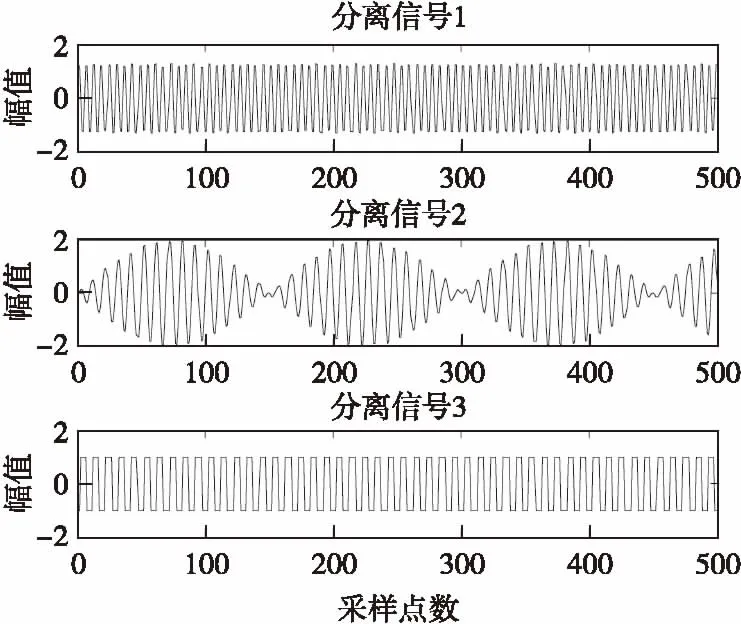
图3 分离信号(改进鲸鱼算法)Fig.3 Separated signals(WOA)

图4 分离信号(粒子群算法)Fig.4 Separated signals(PSO)

图5 算法收敛曲线Fig.5 Algorithm convergence curve
由图1、图3、图4可见,分离信号存在幅度和排列顺序的不确定性,但这不影响分离效果。从图5的收敛曲线对比图中可以看出,经过18步迭代,鲸鱼算法的适应度已经收敛,而且从收敛曲线上看出收敛速度非常快;而粒子群算法在25步左右才收敛,收敛速度相对鲸鱼算法,相对较慢。
选择相似系数ζij作为指标,判断分离效果:
(24)

实验二:加噪情况下,为了验证不同信噪比对提出算法分离性能的影响,设置蒙特卡洛实验,实验信号同实验一,对混合信号作加噪处理,信噪比线性变化范围从-10 dB以步长5到40 dB,每个信噪比下进行100次实验,以串音误差(PI)作为观测值,100次实验取平均值作为当前信噪比下的串音误差,并与粒子群算法进行对比。
串音误差PI定义如下:
(25)
式(25)中,gij是矩阵G第i行第j列的元素,G=WVA,V是混合信号的白化矩阵,PI值越接近0说明算法分离精度越高,实验结果如图6。

图6 盲分离性能随信噪比的变化情况Fig.6 Blind separation performance versus SNR
从图6可见,随着输入信噪比的升高,本文算法与粒子群算法的计算误差逐渐降低,在信噪比低于20 dB时变化尤为明显,此时,本文算法的计算精度更高,分离效果更明显;在信噪比高于20 dB后,两种算法的计算精度趋于一致,都有很好的分离性能。
4 结论
本文提出了基于改进鲸鱼优化算法的盲源分离方法。该方法利用独立性准则,以混合信号的峰度作为目标函数,用鲸鱼优化算法代替常规的粒子群算法,并引入自适应权重,加快收敛速度,实现了对瞬时混叠信号的盲分离,有效地避免了粒子群算法参数复杂、收敛速度慢的问题。仿真对比结果表明,本文方法简单高效,分离精度和收敛速度相较于粒子群算法有明显优势,在更低信噪比下也有良好的分离效果,适用于盲信号分离,可为盲信号处理提供一种新的研究思路与方法。

