矩形与三角布阵阵元失效影响对比*
万 康
(中国电子科技集团公司第三十八研究所 合肥 230088)
1 引言
雷达作为一种能主动发射电磁波并接受目标返回的信号来实现对远距离目标进行全天候探测的装备,在军民用许多领域中获得了应用,而相控阵雷达因具有天线波束快速扫描、波束形状可捷变等特点获得了长足进步[1~2]。相当一部分相控阵雷达采用的是平面相控阵天线,平面相控阵的天线排列方式主要有矩形排列和三角形排列,在面积相同且同样不产生栅瓣的条件下,天线单元总数三角形排列比矩形排列大约少10%以上[3~7]。
相控阵天线不可避免存在阵元失效的情况,阵元失效所造成的影响有副瓣抬高、增益下降等,对天线性能有不可忽视的影响,在机载、星载、紧急使用等情况下阵元失效往往来不及替换,许多分析聚焦于在不替换阵元的情况下对失效后的阵面进行校正或重构,因此有效评估阵元失效的危害程度来判断校正或重构是否可行具有重要意义[8~15]。天线阵元失效模式与系统内部组成有密切关系,为了简化分析,仅考虑阵面的阵元失效影响。对于直线阵列和矩形排布形式的阵元失效影响分析已有较多的分析[16~21],而对于常用的三角形排布天线的阵元失效影响分析却较少,探索三角形排布天线的阵元失效影响具有重要的意义。
本文在分析矩形布阵的情况下构建了与矩形阵列口径相同面积的正三角形排布天线,由于阵元失效主要影响副瓣电平[14~21],因此分析了阵列天线的副瓣电平与失效阵元位置之间的关系,与矩形排布作对比,得出了一些结论,该分析结果为具有失效阵元的阵列天线诊断修复奠定了基础,为两种布阵方式的选择提供了一些依据。
2 矩形与三角布阵基础
模型坐标系建立如图1所示,设阵列平面位于xy平面,阵列波束指向OP与z轴正半轴夹角为θ,OP在xy平面上的投影为OP1,OP1与x轴正半轴的夹角为φ,波束指向即可以用球坐标(θ,φ)表示。在图中,xy平面上的阵面为矩形布阵,设x轴方向的阵元数为Nx,阵元间距为dx,y轴方向的阵元数为Ny,阵元间距为dy,波束指向OP与x轴、y轴正半轴夹角分别为αx、αy,有

其中 0≤θ≤π/2,0≤φ≤2π。一般记u=cos(αx),v=cos(αy)。


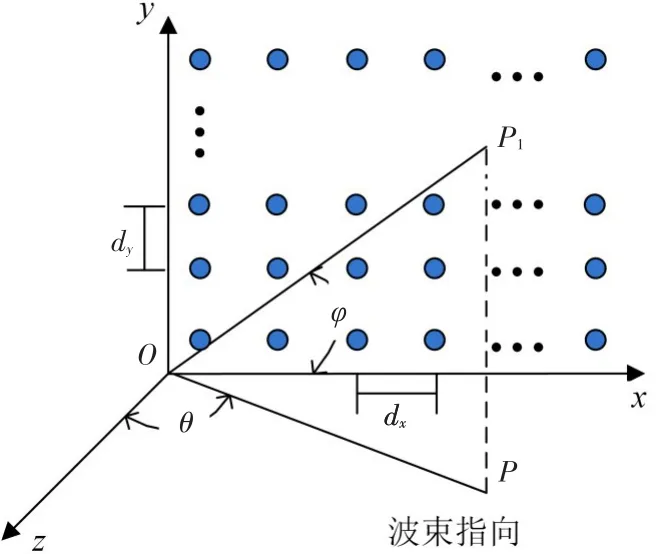
图1 矩形平面阵及其坐标系

当阵面阵元排布为正三角形时,为了比较矩形排列与三角形排列的性能差异,构建了与矩形阵列口径相同面积且同样不产生栅瓣的条件下的正三角形排列天线,如图2所示,为了表示方便,将三角排布的间隙填充构成矩形排布,其中灰色点为实阵元,进行馈电,白色点为虚拟阵元,馈电幅度置0。在求方向图函数时三角形平面阵列天线可以看做两个矩形阵面之和,在其中任一矩形阵面中x轴、y轴方向的间距分别为2dx、2dy,阵元个数分别为Nx1、Ny1,天线的方向图函数F(cosαx,cosαy)为
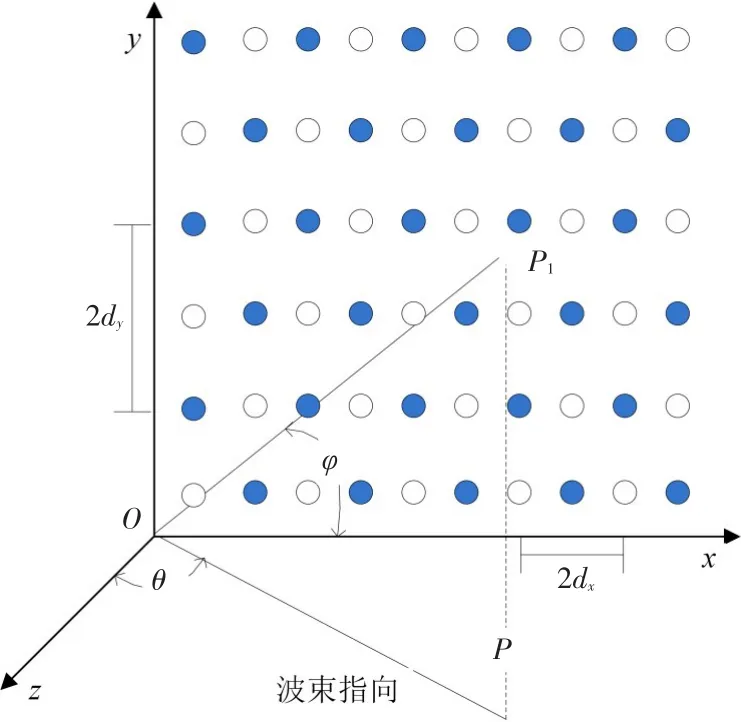
图2 三角形排列平面阵

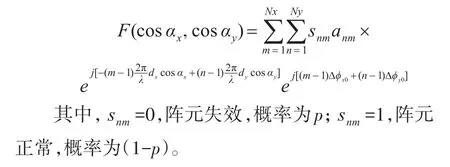

3 低副瓣加权分析
阵列的低副瓣特性对雷达系统的性能有着至关重要的影响,为改善副瓣性能会对阵元进行加权等操作,常见的加权函数有均匀加权、Hamming加权、Chebyshev加权、Taylor加权等,如何加权需要因雷达需求而作具体分析。为了满足矩形布阵和三角布阵的低副瓣要求,分析了常用的Chebyshev加权和Taylor加权。
按图1所示来布置矩形阵列,阵元数Nx=32,Ny=32,阵元间距dx、dy均为0.5λ(λ为波长),扫描角均为0°。取阵面均匀加权、-30dB副瓣Chebyshev加权、Taylor加权沿x、y轴方向的方向图作比较,如图3、图4所示,所画三维图为(u,v)坐标。
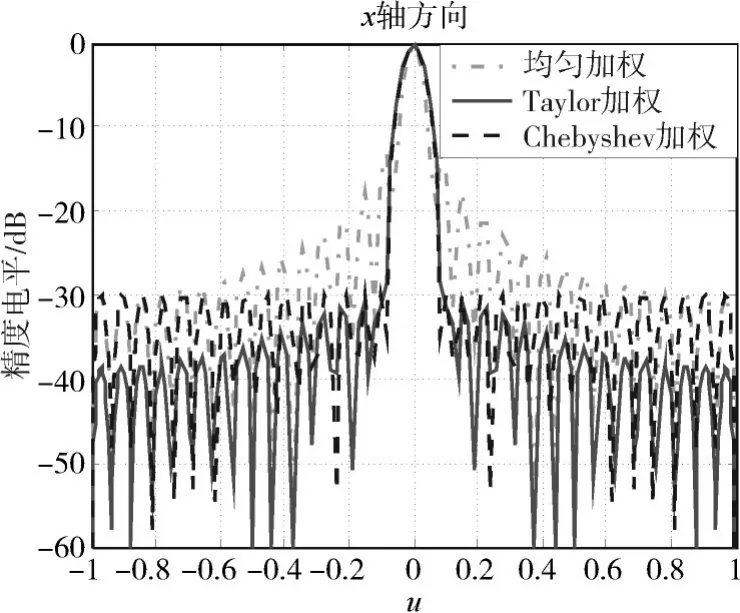
图3 几种加权方式沿x轴方向方向图的对比
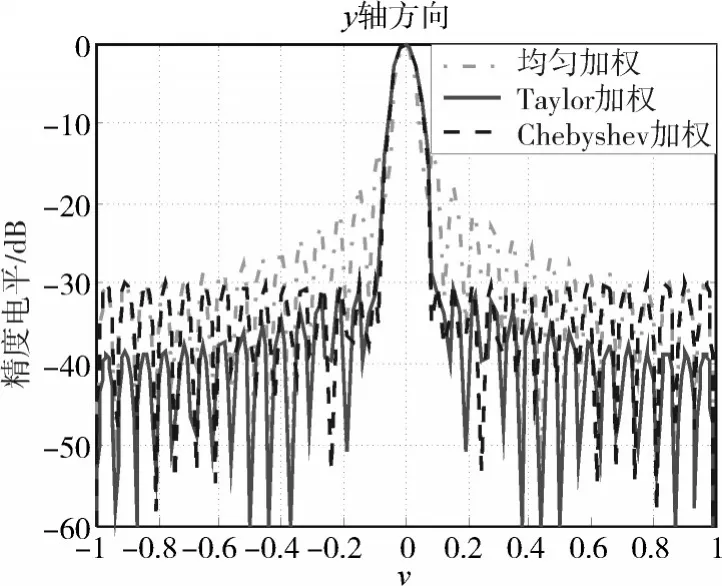
图4 几种加权方式沿y轴方向方向图的对比
同理,按图2所示来布置三角形栅格阵面,阵面大小与上述矩形栅格阵面相同,按上述不产生栅瓣条件的分析设定参数,扫描角均为0°,沿x、y轴方向的总阵元数分别为57、33,其中实阵元数约占矩形排布阵元总数的92%,比矩形排布阵元总数少约8%。加权方式按照三角形栅格填充成完整矩形阵面时的加权进行并将填充单元置零,取阵面均匀加权、-30dB副瓣Chebyshev加权、Taylor加权沿x、y轴方向的方向图作比较,如图5、图6所示。
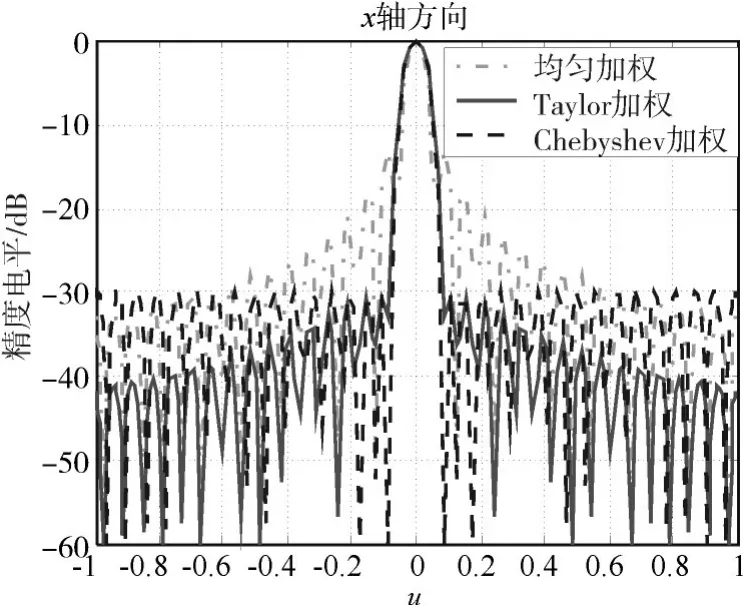
图5 几种加权方式沿x轴方向方向图的对比
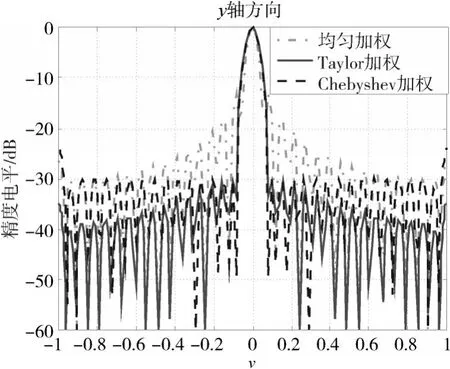
图6 几种加权方式沿y轴方向方向图的对比
由上述图形可以看出,矩形布阵时-30dB副瓣Chebyshev加权、Taylor加权在沿x、y轴方向均能取得良好效果,Chebyshev加权、Taylor加权的主瓣形状及宽度几乎相同,Taylor加权方向图主瓣附近的副瓣略微保持恒定,但远离主瓣的副瓣类似均匀加权天线阵逐渐下降的特性,Chebyshev加权在沿x、y轴方向均保持了恒定的-30dB副瓣特性。三角形布阵时-30dB副瓣Chebyshev加权、Taylor加权在沿x轴方向的特性与矩形布阵相似,但在沿y轴方向有较大不同,沿y轴方向均匀加权、-30dB副瓣Chebyshev加权、Taylor加权的方向图会出现在稀疏维v=±1区域相对于矩形排布方向图“翘起”的反常现象,导致Chebyshev加权恒定的-30dB副瓣特性变差约5dB,为了消除其对副瓣影响,本文采用Taylor加权来分析。
4 单阵元失效分析
下面先选择总阵元数量较少的情况来分析单阵元失效,找出一般规律来推导到比较符合实际总阵元数量较多的情况。
4.1 矩形排列阵面
按图1所示来布置矩形阵列,阵元数Nx=8,Ny=8,进行Taylor加权,扫描角均为0°,无阵元失效时沿x轴、y轴方向的方向图副瓣电平均为-28.3dB。单个阵元主要对副瓣电平影响较大,单阵元失效沿x轴、y轴方向的相对无失效时的副瓣电平如图7、8所示,Nx、Ny为图1中不同位置对应的阵元,左上角记为(1,1),以此类推。
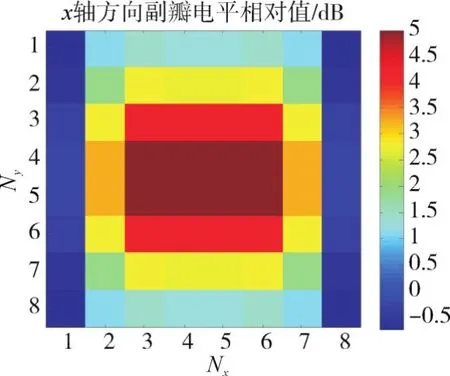
图7 沿x轴方向相对于无失效时的副瓣电平
由图中可知,相对于无失效副瓣电平-28.3dB,单阵元失效时的副瓣电平变化范围在-0.7dB~5dB,失效占比约为1.6%,越靠近阵元中心的位置副瓣抬高值越大,抬高最大值约为5dB,靠近边缘位置副瓣略有约-0.7dB的下降,即单阵元失效时副瓣抬高的概率更大。

图8 沿y轴方向的相对无失效时的副瓣电平
4.2 三角形排列阵面
下面构建与矩形阵列相同面积且同样不产生栅瓣的三角排列天线,按图2所示布阵,扫描角均为0°,进行Taylor加权。沿x、y轴方向的总阵元数分别为14、8,其中实阵元数比矩形排布阵元总数少约12%,所画三维图为坐标(u,v),其中沿x轴、y轴方向的方向图副瓣电平分别为-30.0dB、-25.9dB。单阵元失效沿x轴、y轴方向的相对无失效时的副瓣电平如图9、10所示,虚拟阵元处数值设为0dB,无实际意义。

图9 沿x轴方向相对于无失效时的副瓣电平
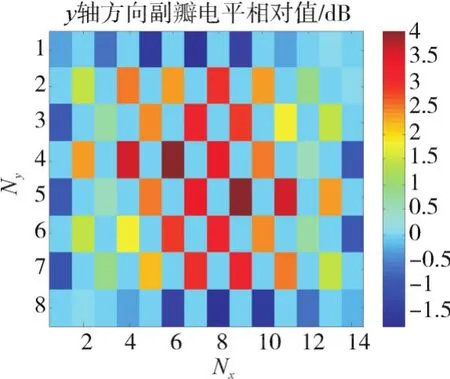
图10 沿y轴方向相对于无失效时的副瓣电平
由图中可知,阵元失效沿x轴、y轴方向的相对无失效时的副瓣电平有较大差异,单阵元失效占总阵元数比例约为1.8%,单阵元失效时沿x轴方向相对无失效的副瓣电平变化范围在0~7.3dB,越靠近阵元中心的位置副瓣抬高值越大,抬高最大值约7.3dB,总体上副瓣均有所抬高。沿y轴方向相对无失效的副瓣电平变化范围在-1.8dB~4dB,越靠近阵元中心的位置副瓣抬高值越大,抬高最大值约4dB,靠近边缘位置副瓣略有约-1.8dB的下降,总体上单阵元失效时副瓣抬高的比例更大。
4.3 两种布阵方法比较
两种布阵的共同点是阵元失效越靠近阵元中心的位置副瓣抬高越大,矩形与三角布阵两种失效占总阵元数比例分别为1.6%、1.8%,在中心位置造成沿x轴方向的副瓣电平分别为-23.3dB、-22.7dB,沿y轴方向的副瓣电平分别为-23.3dB、-21.9dB。
5 多阵元失效
实际应用中阵面规模一般较大,远不止8行×8列单元规模,且失效单元不止一个,可能存在多个阵元失效并随机分布在阵面上,此时评估阵元失效的危害程度来判断校正或重构是否可行要考虑多种失效分布情况,本文根据前面分析的位于中心区域阵元失效影响最大的特点,假设失效阵元全部位于中心位置,得出最坏的情况,评估不同阵面规模失效率对副瓣的影响,选取了矩形排布32行×32列、48行×48列、64行×64列等三种情况,参数设置按第3节,按上面使用的方法产生同面积且同样不产生栅瓣条件的分析设定三角布阵参数,对应的三角布阵虚实阵元排布分别为33行×57列、49行×85列、65行×113列,其中实阵元数对应约为33×57/2、49×85/2、65×113/2,阵元数减少分别为8%、10%、10%,分别作出矩形布阵和三角布阵阵元失效占比沿x轴、y轴方向的最大副瓣电平值,如图11~14。
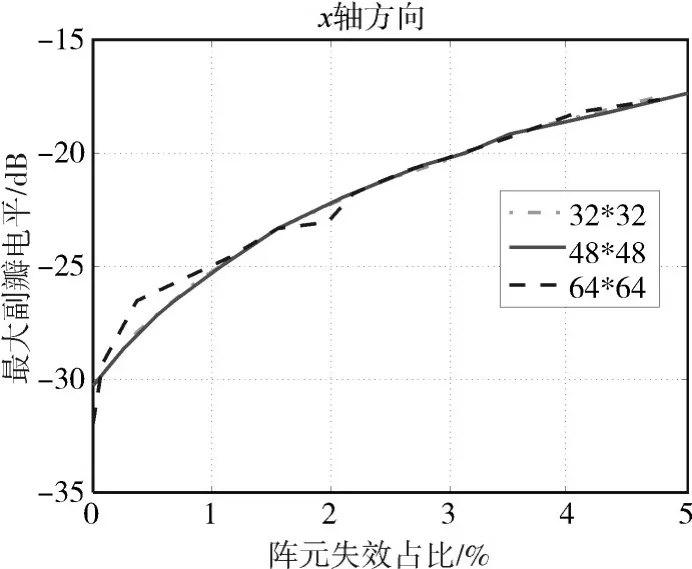
图11 矩形布阵x轴方向副瓣电平与阵元失效率关系
图中可以看出,矩形布阵和三角布阵的最大副瓣电平与阵元失效占比基本上成正比关系,在Taylor加权时矩形布阵和三角布阵两者的曲线基本拟合,在阵元失效占比从0%~5%递增时两者沿x轴、y轴方向的最大副瓣电平值约从-31dB减小到-18dB。若以-20dB的最大副瓣电平值为要求,则阵元失效率在3%即可满足要求,实际阵元失效并不会全在中心位置,以-20dB的副瓣电平值要求的失效率可能大于3%。两种布阵都是平面阵列重要的排布形式,实际应用时结合要求进行选择。
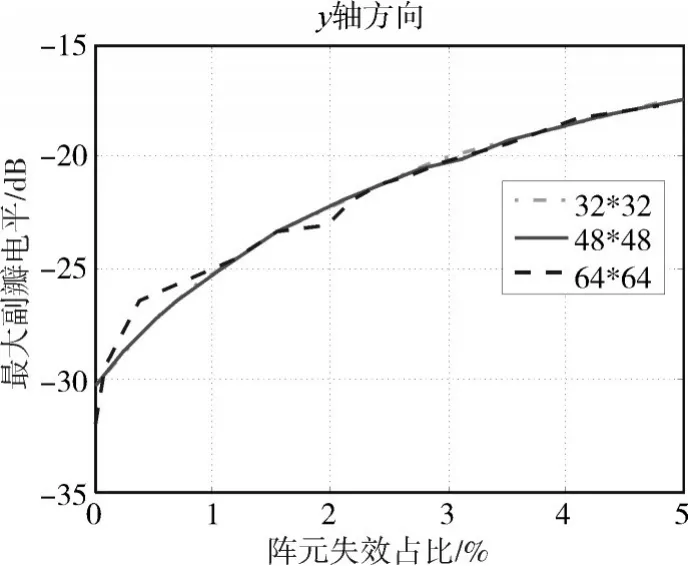
图12 矩形布阵y轴方向副瓣电平与阵元失效率关系
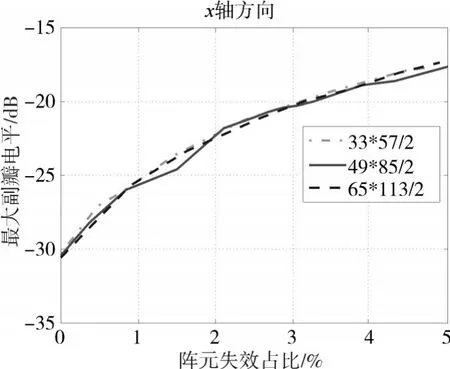
图13 三角布阵x轴方向副瓣电平与阵元失效率关系
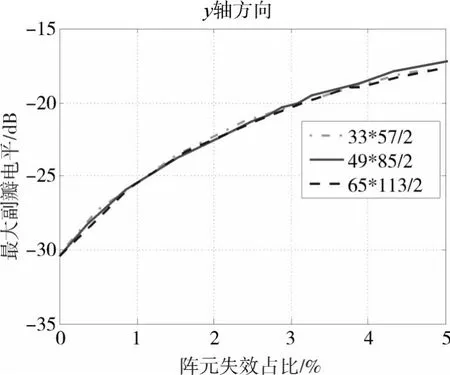
图14 三角布阵y轴方向副瓣电平与阵元失效率关系
6 结语
本文首先以相同面积同样不产生栅瓣条件的矩形排列和三角形排列天线为模型来分析单阵元失效对平面阵列天线副瓣的影响,得出了中心位置阵元失效对副瓣抬高影响更大,然后以32×32、48×48、64×64等三种情况矩形排布及对应的三角形排布的中心位置多阵元失效为切入点分析了阵元失效率与最大副瓣电平的关系,给出了两种布阵方式的异同点,为阵列天线的修复校正提供了一定依据。在实际应用过程中会受到多种误差等的影响,下一步将在本文分析基础上,研究其对阵列天线性能的影响及校正方法。

