一种局部优化的粒子群低副瓣波束形成方法

崔 伟，张 冰，余 岚

（1.中国船舶重工集团公司 第722 研究所，湖北 武汉 221116；2.江苏科技大学，江苏 镇江 212003）

0 引 言

低副瓣技术就是使用幅度和相位加权方法来降低波束副瓣电平，提高主副瓣电平比，达到给定方向图的要求[1]。通过粒子群低副瓣技术对方向图优化获得所需的波束主副瓣比，不断向最优解靠近，经过若干次更新之后，即可得到优化的低副瓣波束。在现有的工程中，引用粒子群低副瓣综合技术，能在不改变主瓣宽度的前提下，有效降低副瓣电平，具有实际应用价值。

粒子群低副瓣技术的研究在近几年有了新的成果，将粒子群低副瓣技术应用到天线设计中，从影响天线各阵元之间的耦合因素入手，结合粒子群算法形成一种新的思路，设计优化天线阵馈电幅度，最终仿真和实物实验都达到低副瓣的效果[2]。用粒子群低副瓣技术解决实际工程应用问题，为了减小实际工程中相控阵雷达的发射副瓣电平，设计了一种有实际应用价值的，基于粒子群的唯相位加权法来减小方向图最大副瓣电平[3]。融合其他算法的粒子群低副瓣技术，在粒子群算法基础上结合混沌搜索技术提出一种优化算法，在仅考虑相位加权的情况下，控制阵列天线各单元的馈电相位值，实现宽零陷低副瓣波束赋形[4]。本文针对粒子群算法局部最优的缺陷进行改进，结合聚类分组的思路，实现阵列天线低副瓣赋形。

1 信号模型

对于阵元数为N的一维等间距天线，阵元各向同性，阵元间距为d，方向图函数可以表示为：

式中：wi为加权向量；λ为信号波长；θ为扫描角。

不同的加权向量wi会影响波束方向图的形成效果，使用粒子群进行低副瓣赋形就是不断更新阵元的加权向量wi，使用迭代优化的方法形成所需的低副瓣波束形状。

在Q维空间中，有M个粒子，其中第i(i=1,2,…,M)个粒子位置和速度分别表示为x(i)=(xi1,xi2,…,xiQ)，v(i)=(vi1,vi2,…,viQ)，第i个粒子搜索到的个体极值记为pbi=(pbi1,pbi2,…,pbiQ)，粒子群全体更新得到的全局最优记为gb=(gb1,gb2,…,gbQ)，群体中各个粒子按式（2）、式（3）更新[5]：

式中：q是向量维数；t是迭代次数；c1，c2是加速常数，指粒子跟踪自己和群体最优值的权重；r1，r2是介于[ 0 ,1]的均匀分布随机数；ω是保持原速的系数，即加权向量。

加权向量ω是一个重要的可调整参数，它决定了粒子前后速度vt与vt+1之间影响力的大小，直接反映了算法全局搜索和局部搜索的能力强弱。目前寻找合适加权向量的方法主要有两类：线性法和非线性法。线性法的优点是算法开始重点全局搜索，之后着重局部开发，能提升收敛速度，如式（4）是典型线性递减法。但是线性递减方法一旦陷入局部最优就很难跳出，而非线性方法可以克服这个问题，如带控制因子的非线性递减法，式（5）中控制因子d1=0.2，d2=0.7。

2 粒子群聚类分组的最优方法

粒子群算法易陷入局部最优，在低副瓣波束赋形研究中存在缺陷。本文在标准粒子群算法的基础上提出改进算法，使用优化公式产生一个竞争粒子，判断评价竞争粒子与当前全局最优粒子的优越性，若优于全局最优粒子，则竞争粒子成为新的全局最优粒子，否则重新进入下一次迭代产生新的竞争粒子，继续判断优越性，直到找到新的全局最优粒子，或者达到最大迭代次数为止[6]。这种算法能防止早熟收敛、促进收敛速度，使用周期性最优机制改变粒子群的全局最优粒子，有效地跳出局部最优循环，再使用分组的方式，提高粒子种群的多样性，保障粒子群的收敛速度[7]。

标准粒子群算法易陷入局部最优。为了避开粒子群算法的这种早熟现象，使用一种周期性改变粒子群全局最优粒子的办法：规定粒子群当前全局最优粒子的最大周期为C，假设粒子群中有一个粒子连续成为全局最优粒子的次数大于C，则产生一个竞争粒子，将这个竞争粒子和当前全局最优粒子比较，若更优，则用竞争粒子代替全局最优粒子，否则继续寻找新的竞争粒子，直到找到新的全局最优粒子，或者达到最大迭代次数为止。

在粒子群算法中引入聚类分组的改进方法，这种方法能提高粒子群多样性，从而保障粒子群的收敛速度。本文采用聚类分组变异机制，当全局最优粒子存在时间大于周期限制C时，将粒子群分成k组，根据下式产生竞争粒子。

使用非线性递减法取加权向量ω的值：

式中，一般选用系数ωstart=0.9，ωend=0.4。

粒子群聚类分组最优方法的实现步骤如下：

1）初始化：初始化M个粒子寻找低副瓣波束最优解，随机生成一个含M个粒子的种群，每个粒子有初始状态，标准粒子群算法的加速常量为c1，c2，迭代次数为t，加权向量为ω，最大迭代次数为T，规定全局最优粒子最大周期为C，将种群分成k组产生竞争粒子。

2）根据标准粒子群算法式（2）、式（3）计算更新当前个体极值、全局最优解，即当前低副瓣波形最优解。

3）判断全局最优粒子是否改变，若当前全局最优粒子不变，则计数c=c+1，否则，计数c=1。

4）当一粒子连续成为全局最优粒子次数大于全局最优粒子最大周期C，即c＞C时，将粒子群分成k组，根据式（6）产生竞争粒子。此步骤是为了避免低副瓣波形最优解陷入局部最优，在此条件下产生新的解。

5）比较竞争粒子和全局最优粒子，若竞争粒子更优，则用新的竞争粒子代替当前全局最优粒子，c=1，否则，保持当前全局最优粒子c=c-1，判断新产生的解是否能代替当前低副瓣波形最优解。

6）重复步骤2）～步骤5），直到达到最大迭代次数t为止，算法结束。

流程图如图1 所示。

3 粒子群低副瓣仿真分析

仿真环境及参数设置：阵列天线采用16 元一维线阵，目标副瓣电平[8]为30 dB。在使用粒子群低副瓣赋形时，选用加速常数c1=c2=2，r1，r2取[ 0 ,1 ]间的随机数，向量维数[4]q=100，最大进化迭代次数为100，粒子群当前全局最优粒子的最大周期C=5。

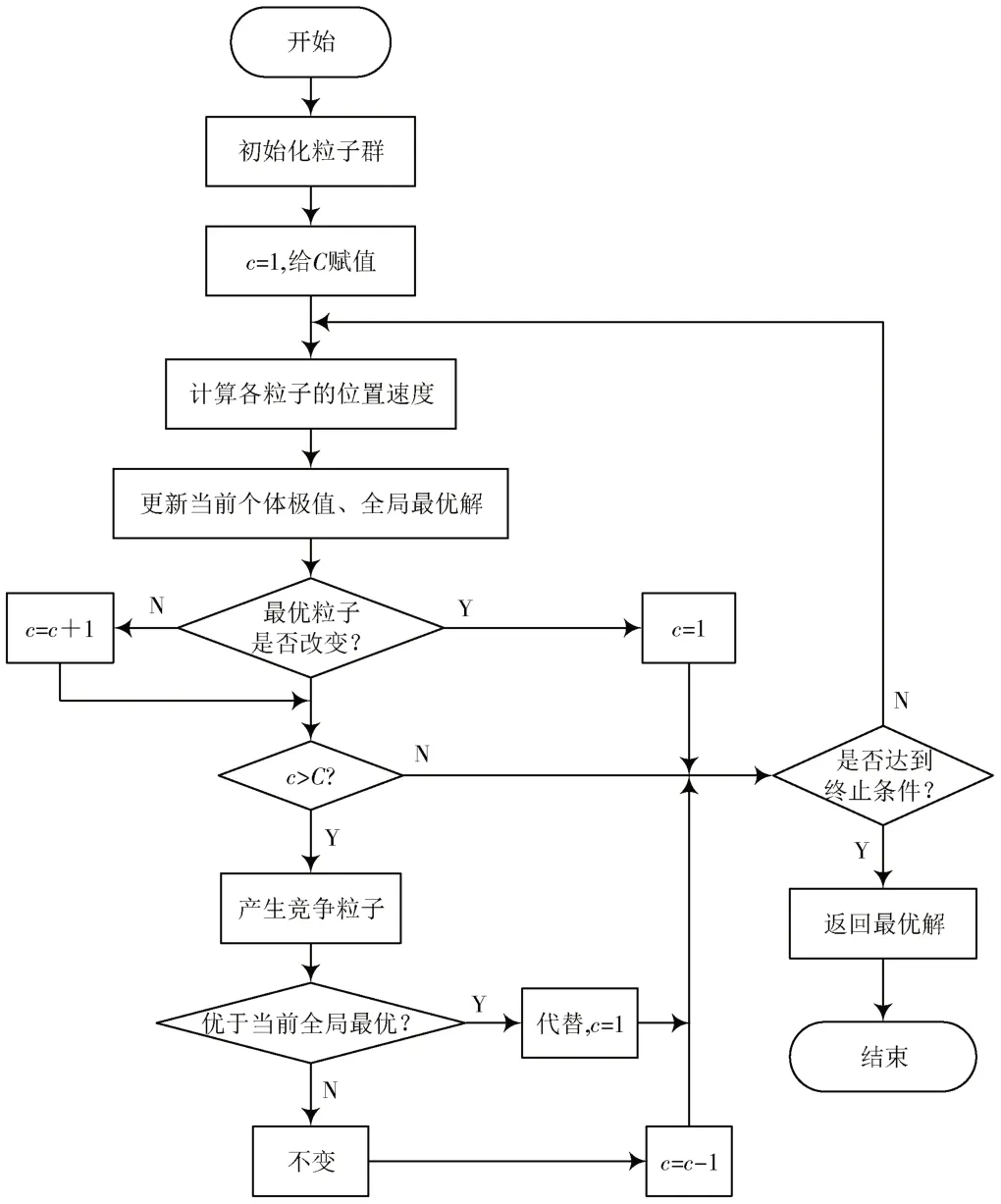
图1 粒子群聚类分组算法流程图

使用经典粒子群算法和局部优化的粒子群算法均可实现低副瓣波束赋形[9]，其迭代的收敛参数见表1。从表1 可以看出，局部优化后的粒子群算法在阵列天线实现低副瓣过程中有较好的全局收敛能力，其收敛速度和精度都有明显的优势。

图2，图3 分别给出了两种算法的最佳适应度随迭代次数变化的曲线，图中纵坐标为适应度的对数值。从图2 中可以看出，粒子群算法在迭代20 次左右，出现局部最优现象，此后算法优化失效，而改进粒子群算法在出现短暂停滞后恢复优化效果，对阵列天线低副瓣效果的实现更好。

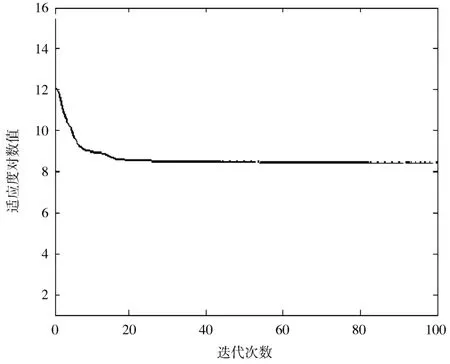
图2 粒子群算法适应度变化曲线

表1 算法迭代过程参数比较

图3 改进粒子群算法适应度变化曲线

图4 为基于粒子群算法仿真得到的低副瓣方向图，图5 为基于局部优化的粒子群算法仿真得到的低副瓣方向图，相较于图4 有更低、更平稳的方向图副瓣电平，且稳定值低于30 dB，达到了低副瓣的设计要求，有效实现了低副瓣赋形。这说明局部优化的粒子群算法确实解决了粒子群算法局部最优的缺陷，又有较快的优化能力，能更快、更有效地实现阵列天线低副瓣赋形。

4 结 语

在阵列天线低副瓣赋形研究过程中，发现使用粒子群算法得到的波束方向图副瓣电平达不到低副瓣要求且不稳定。为了能够快速稳健地形成阵列天线低副瓣波束，本文提出了一种周期性改变全局最优粒子的粒子群算法，仿真结果表明，在阵列天线低副瓣赋形中，这种局部优化算法克服了经典粒子群算法易陷入局部最优的缺点，提高了迭代速度和波束赋形的稳定性，具有较大的实际应用价值。

图4 经典粒子群算法的低副瓣方向图

图5 局部优化粒子群算法的低副瓣方向图